미로만들기 - 2665번
문제
n×n 바둑판 모양으로 총 n2개의 방이 있다. 일부분은 검은 방이고 나머지는 모두 흰 방이다. 검은 방은 사면이 벽으로 싸여 있어 들어갈 수 없다. 서로 붙어 있는 두 개의 흰 방 사이에는 문이 있어서 지나다닐 수 있다. 윗줄 맨 왼쪽 방은 시작방으로서 항상 흰 방이고, 아랫줄 맨 오른쪽 방은 끝방으로서 역시 흰 방이다.
시작방에서 출발하여 길을 찾아서 끝방으로 가는 것이 목적인데, 아래 그림의 경우에는 시작방에서 끝 방으로 갈 수가 없다. 부득이 검은 방 몇 개를 흰 방으로 바꾸어야 하는데 되도록 적은 수의 방의 색을 바꾸고 싶다.
아래 그림은 n=8인 경우의 한 예이다.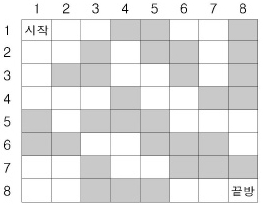 위 그림에서는 두 개의 검은 방(예를 들어 (4,4)의 방과 (7,8)의 방)을 흰 방으로 바꾸면, 시작방에서 끝방으로 갈 수 있지만, 어느 검은 방 하나만을 흰 방으로 바꾸어서는 불가능하다. 검은 방에서 흰 방으로 바꾸어야 할 최소의 수를 구하는 프로그램을 작성하시오.
위 그림에서는 두 개의 검은 방(예를 들어 (4,4)의 방과 (7,8)의 방)을 흰 방으로 바꾸면, 시작방에서 끝방으로 갈 수 있지만, 어느 검은 방 하나만을 흰 방으로 바꾸어서는 불가능하다. 검은 방에서 흰 방으로 바꾸어야 할 최소의 수를 구하는 프로그램을 작성하시오.
단, 검은 방을 하나도 흰방으로 바꾸지 않아도 되는 경우는 0이 답이다.
입력
첫 줄에는 한 줄에 들어가는 방의 수 n(1 ≤ n ≤ 50)이 주어지고, 다음 n개의 줄의 각 줄마다 0과 1이 이루어진 길이가 n인 수열이 주어진다. 0은 검은 방, 1은 흰 방을 나타낸다.
출력
첫 줄에 흰 방으로 바꾸어야 할 최소의 검은 방의 수를 출력한다.
풀이
다음의 코드는 정답이다.
풀이의 원리는 다익스트라 알고리즘이다.
import sys
import heapq
input = sys.stdin.readline
N = int(input())
graph = [[] for _ in range(N)]
for i in range(N):
graph[i] = list(map(int, input().rstrip()))
visit = [[0] * N for _ in range(N)]
visit[0][0] = 1
heap = []
heapq.heappush(heap, [0, 0, 0])
dx = [1, -1, 0, 0]
dy = [0, 0, -1, 1]
def dijkstra():
global heap
while heap:
cnt, x, y = heapq.heappop(heap)
if x==N-1 and y==N-1:
print(cnt)
return
for i in range(4):
nx = x+dx[i]
ny = y+dy[i]
if 0<=nx< N and 0<=ny< N and visit[nx][ny]==0:
visit[nx][ny] = 1
if graph[nx][ny]==0:
heapq.heappush(heap, [cnt+1, nx, ny])
else:
heapq.heappush(heap, [cnt, nx, ny])
dijkstra()