DFS와 BFS - 1260번
문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
풀이
이는 너비 우선 탐색Bfs과 깊이 우선 탐색Dfs에 대한 이미지이다.(보통 dfs 먼저 나오는데 이건 왜 좌우가 순서가 다른 것이야...)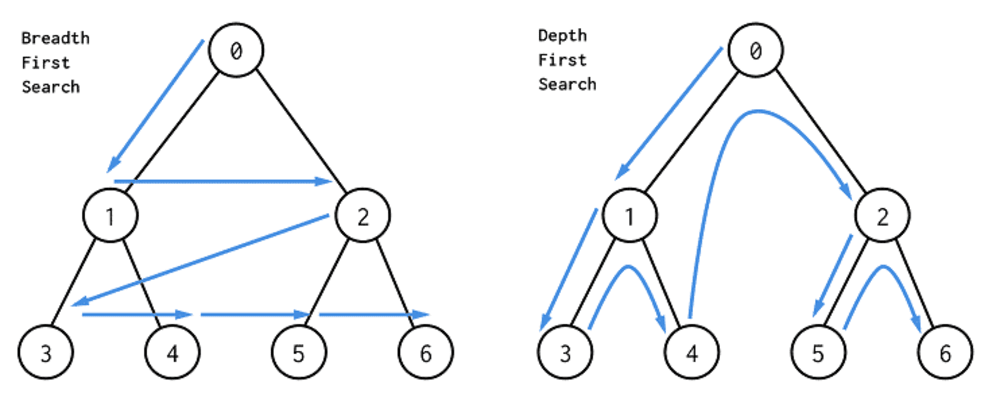
순회에 대해 다시 떠올려보자 .이젠 dfs가 전위 순회(Preorder traverse), bfs가 층별 순회(level order traverse)임을 알 수 있다.
이진 트리 순회(Tree Traverse)
⊙ 전위 순회(preorder traverse) : 뿌리(root)를 먼저 방문
⊙ 중위 순회(inorder traverse) : 왼쪽 하위 트리를 방문 후 뿌리(root)를 방문
⊙ 후위 순회(postorder traverse) : 하위 트리 모두 방문 후 뿌리(root)를 방문
⊙ 층별 순회(level order traverse) : 위 쪽 node들 부터 아래방향으로 차례로 방문
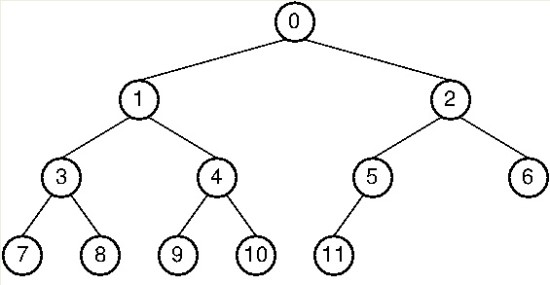
전위 순회 : 0->1->3->7->8->4->9->10->2->5->11->6
중위 순회 : 7->3->8->1->9->4->10->0->11->5->2->6
후위 순회 : 7->8->3->9->10->4->1->11->5->6->2->0
층별 순회 : 0->1->2->3->4->5->6->7->8->9->10->11
★전위 순회는 뿌리->왼쪽 자식->오른쪽 자식 순
★중위 순회는 왼쪽자식-> 뿌리-> 오른쪽 자식
★후위 순회는 왼쪽자식->오른쪽 자식-> 뿌리
★층별 순회는 그냥 노드의 순서대로
dfs 함수는 재귀 함수, bfs 함수는 큐를 이용하여 구현한다.
다음의 코드는 정답이다.
import sys
from collections import deque
input = sys.stdin.readline
N, M, V = map(int, input().split())
graph = [[0] * (N+1) for _ in range(N+1)]
visited2 = [0] * (N+1)
visited1 = [0] * (N+1)
for _ in range(M):
a, b = map(int, input().split())
graph[a][b] = graph[b][a] = 1
# print(graph)
def dfs(v):
visited1[v] = 1
print(v, end=" ")
for i in range(1, N+1):
if visited1[i]==0 and graph[v][i]==1:
dfs(i)
def bfs(v):
q = deque()
q.append(v)
visited2[v] = 1
while q:
v = q.popleft()
print(v, end=" ")
for i in range(1, N+1):
if visited2[i]==0 and graph[v][i]==1:
q.append(i)
visited2[i] = 1
dfs(V)
print()
bfs(V)인접(adjacent) : 두 정점을 연결하는 간선이 있을 때, 서로 인접하다고 한다.
부속(incident) : 인접한 두 정점 사이의 간선은 두 정점에 부속되었다고 말한다.
차수(degree) : 정점에 부속되어 있는 간선의 수.
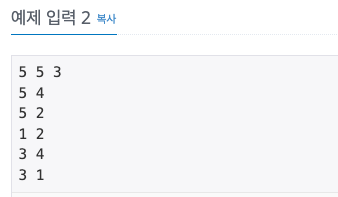 예제입력2를 입력하여 graph를 만들면 아래와 같은 행렬이 된다.
예제입력2를 입력하여 graph를 만들면 아래와 같은 행렬이 된다.
graph = [
[0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 0],
[0, 1, 0, 0, 0, 1],
[0, 1, 0, 0, 1, 0],
[0, 0, 0, 1, 0, 1],
[0, 0, 1, 0, 1, 0]
]인접 행렬(adjacency matrix)은 그래프에서 어느 꼭짓점들이 변으로 연결되었는지에 대한 데이터를 표현한 정사각 행렬이다.
# 인접 행렬 만들기.
graph = [[0] * (N+1) for _ in range(N+1)]
visited2 = [0] * (N+1)
visited1 = [0] * (N+1)
for _ in range(M):
a, b = map(int, input().split())
graph[a][b] = graph[b][a] = 1graph[a][b] = graph[b][a] = 1는, 문제에서 입력으로 주어지는 간선은 양방향이므로 이는 예를 들어 (2, 1)과 (1, 2)는 무조건 값이 같음이다. 이는 철수랑 영희 사이에 간선이 있다 치면 철수도 "네. 영희랑 제 사이에 간선 있음요." 라고 대답할 것이고 영희고 "네. 철수랑 제 사이에 간선 있음ㅇㅇ" 이라고 대답하는 것과 같다.
정점의 갯수+1개만큼의 빈 칸([0])을 가지는 1열짜리 체크표시용 변수 visited가 (인덱스 0번빼고, 왜냐면 이 칸은 안 쓰는 칸) 다 '방문했음'([1])으로 채워졌을 때에, 그 탐색(for문||whlie문)을 끝내는 것이 원리이다.
dfs 디버깅
그래도 찍어먹어본 거라 그런지 bfs보다 코드가 더 직관적이게 느껴지는 것 같다... 아닌가.
1. 함수는 주어진 시작할 정점 V에서부터 탐색을 시작한다. 현재, 변수 v는 V다. 먼저 visited1에 탐색을 시작한 정점번호 V번째 칸에 방문한 표시, V를 방문했다고 출력해준다.
2. 그런 뒤 for문으로 graph의 V번째 열의 정보를 확인하는 거다. 방문 안 되있는데 인접해있다고 되있는 인접 정점번호가 나오면, 곧장 그 정점으로 이동해 그 정점번호를 방문했음이라고 visited1에 표시, 그 정점번호 출력, 거기서부터 또 탐색. 이러는 거다.
bfs 디버깅
- 함수는 주어진 시작할 정점 V에서부터 탐색을 시작한다. 현재, 변수 v는 V다. 먼저 visited2에 탐색을 시작한 정점번호 V번째 칸에 방문한 표시를 한다. 이후 인접행렬에서 V번째 열의 내용을 visited2에 담는다. 그럼 이제 for문을 돌면서 큐 변수 q와 방문체크표시용 변수 visited2에 담기는 내용을 같이 확인해볼 수 있다.
- visited2는
아까 탐색을 시작한 정점번호 V와,변수 graph의 그 정점번호 V번째 열에 담긴 정보(== 정점번호 V와 인접해있는 정점번호들)가 함께 합쳐져서 담긴다. q에도 똑같은 정보가 담기는데 다만 아까 for문 들어오기 전에 이미 탐색을 시작한 정점번호 v에 대해선 popleft()로 V를 배출해냈다. 고로 for문이 다 돌려지면 q에는변수 graph의 그 정점번호 V번째 열에 담긴 정보(== 정점번호 v와 인접해있는 정점번호들)만 담겨져 있다! 그렇게 while문 돌이가 한 번 싹 끝난다. - 그렇게 while문의 첨으로 복귀하면 아까 정점번호 v번에서부터 가장 먼저 연결되어있던 다른 정점번호가 변수 v에 담긴다. 현재, 변수 v는 이제 새로운 정점번호다. 그렇게 재할당 된 v번째의 정점에서부터 다시 탐색을 한다.
- for문을 시작할 떄, visited2는
아까 정점번호 V와 인접해있는 나머지 정점번호와,방금 우리가 새 탐색을 시작한 새로운 정점번호 v가 담긴 상태이다. 여기서 이제부터변수 graph의 그 새 정점번호 v번째 열에 담긴 정보(== 정점번호 v와 연결되어 있는 정점번호들)가 함께 합쳐져서 담긴다. 담기는데, visited2는 1열짜리 체크표라서 아까 담아놓은 정보들과 충돌할 시 탐색이 종료되며 그것부터 popleft()된다. 즉 아까 방문했던 정점V를 거른 다음 인접 정점번호부터 출력이 되는 것이다. 그런 식으로 visited2가 하나씩 채워진다, 즉, 하나씩 모든 정점을 방문한다.