Tree (트리)
• 트리는 가계도와 같이 계층적인 구조를 표현할 때 사용할 수 있는 자료구조다.
• 나무(tree)의 형태를 뒤집은 것과 같이 생겼다.
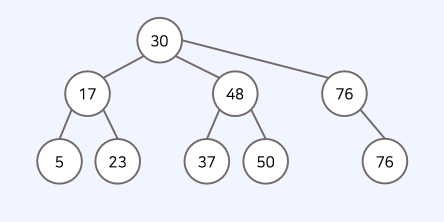
트리 용어 정리 자료구조
• 루트 노드(root node): 부모가 없는 최상위 노드
• 단말 노드(leaf node): 자식이 없는 노드
=> 기본적으로 트리의 크기가 N일 때, 전체 간선의 개수는 N - 1 개 입니다.
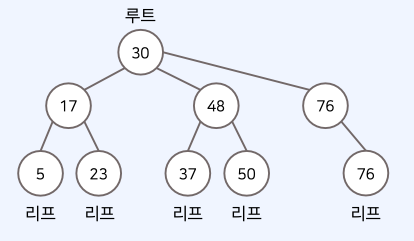
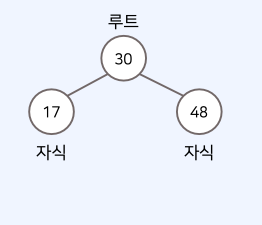
• 트리(tree)에서는 부모와 자식 관계가 성립한다.
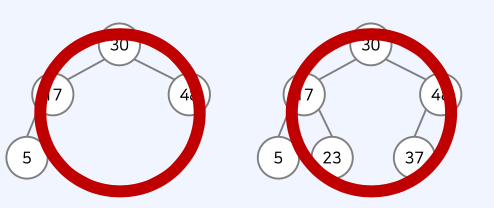
• 형제 관계: 17을 값으로 가지는 노드와 48을 가지는 노드 사이의 관계
• 깊이(depth): 루트 노드에서의 길이(length)
• 이때, 길이란 출발 노드에서 목적지 노드까지 거쳐야 하는 간선의 수를 의미한다.
• 트리의 높이(height)는 루트 노드에서 가장 깊은 노드까지의 길이를 의미한다.
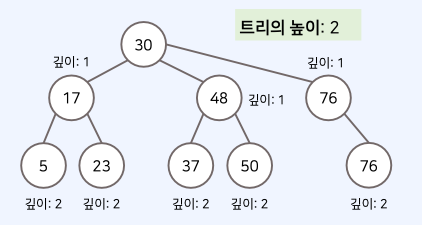
이진 트리(Binary Tree)
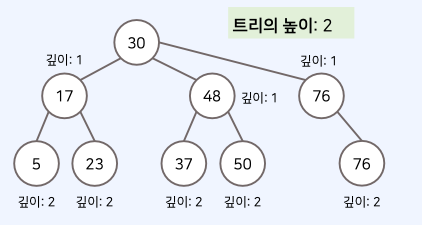
깊이(depth): 루트 노드에서의 길이(length)
• 이때, 길이란 출발 노드에서 목적지 노드까지 거쳐야 하는 간선의 수를 의미한다.
• 트리의 높이(height)는 루트 노드에서 가장 깊은 노드까지의 길이를 의미한다.
• 이진트리는최대2개의자식을가질수있는트리를말한다.
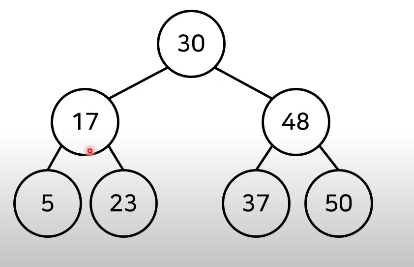
이진 탐색 트리 (Binary Search Tree)
- 이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조의 일종이다.
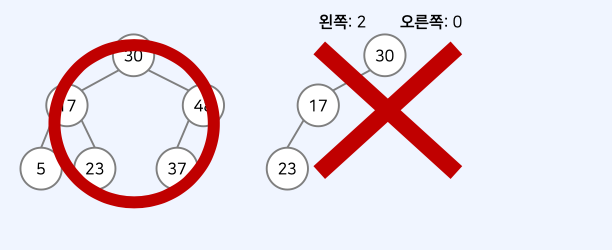
- 이진 탐색 트리의 특징: 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드
- 부모 노드보다 왼쪽 자식 노드가 작습니다.
- 부모 노드보다 오른쪽 자식 노드가 큽니다.
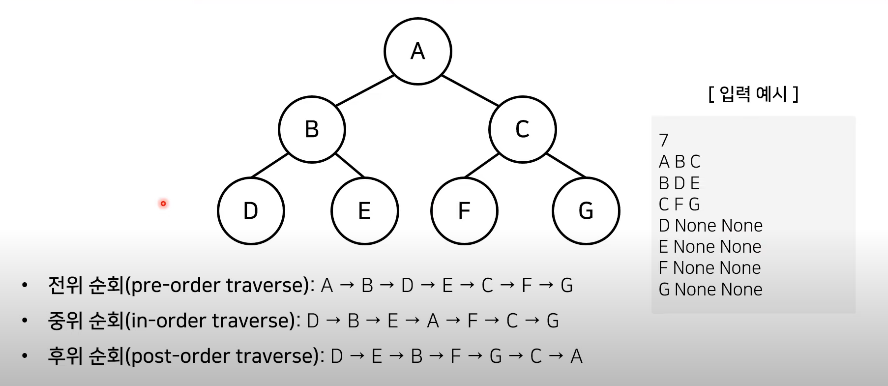
트리의 순회(Tree Traversal)
- 트리 자료 구조에 포함된 노드를 특정한 방법으로 한 번씩 방문하는 방법을 의미한다.
- 트리의 정보를 시각적으로 확인할 수 있다. - 대표적인 트리 순회 방법은 다음과 같습니다.
- 전위 순회(Pre-order traverse): 루트를 먼저 방문한다.- 중위 순회(in-order traverse) : 왼쪽 자식을 방문한 뒤에 루트를 방문한다.
- 후위 순회(post-order traverse) : 오른쪽 자식을 방문한 뒤에 루트를 방문한다.
트리의 순회(Tree Traversal) 구현
class Node:
def_init_(self, data, left_node, right_node):
self.data =data
self.left_node = left_node
self.right_node = right_node
# 전위 순회(Preorder Traversal)
def pre_order(node):
print(node.data, end=' ')
if node.left_node != None:
pre_order(tree[node.left_node])
if node.right_node != None:
pre_order(tree[node.right_node])
# 중위 순회 (Inorder Trabersal)
def in_order(node);
if node.left_node != None:
in_order(tree[node.left_node])
print(node.data, end=' ')
if node.right_node != None:
in_order(tree[node.rigth_node])
# 후위 순회 (Postorder Traversal)
def post_order(node):
if node.left_node != None:
post_order(trree[node.left_nodel])
if node.right_node != None:
post_order(tree[node.right_node])
print(node.data, end= " ")
n = int(input())
tree = {}
for i in range(n);
data, left_node, right_node = input().split()
if left_node === "Node";
left_node = None
if right_node === "None":
three[data] = Node(data, left_node, right_node)
pre_order(tree['A'])
print()
in_order(tree['A'])
print()
post_order(tree['A'])
우선순위 큐(Priority Queue)
• 우선순위 큐는 우선순위에 따라서 데이터를 추출하는 자료구조다.
• 컴퓨터 운영체제, 온라인 게임 매칭 등에서 활용된다.
• 우선순위 큐는 일반적으로 힙(heap)을 이용해 구현한다.
우선순위 큐를 구현하는 방법
• 우선순위 큐는 다양한 방법으로 구현할 수 있다.
• 데이터의개수가𝑁개일때,구현방식에따른시간복잡도는다음과같다.

우선순위 큐를 구현하는 방법
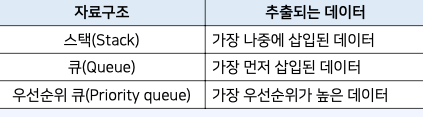
• 일반적인 형태의 큐는 선형적인 구조를 가진다.
• 반면에 우선순위 큐는 이진 트리(binary tree) 구조를 사용하는 것이 일반적이다.
이진 트리(Binary Tree)
• 이진 트리(binary tree)는 최대 2개까지의 자식을 가질 수 있다.
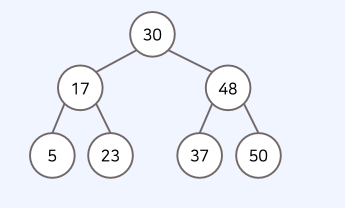
포화 이진 트리(Full Binary Tree)
• 포화이진트리는리프노드를제외한모든노드가두자식을가지고있는트리다.
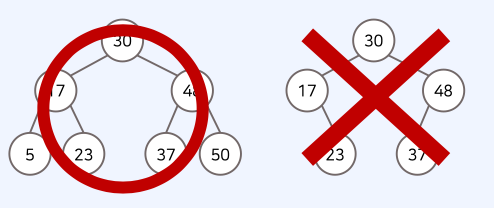
완전 이진 트리(Complete Binary Tree)
• 완전 이진 트리는 모든 노드가 왼쪽 자식부터 차근차근 채워진 트리다.
높이 균형 트리(Height Balanced Tree)
• 왼쪽자식트리와오른쪽자식트리의높이가1이상차이나지않는트리다.