자바스크립트에서 0.1+0.2는 왜 0.3이 아닐까?

서론

자바스크립트에서 0.1 + 0.2 를 하면 0.3이 나올것 같지만, 0.30000000000000004이 나옵니다.
왜 이런 문제가 발생하는 것일까요🤔?

이번 시간에는 부동소수점을 구하는 방법을 알아보고
0.1 + 0.2가 0.3이 나오는지 확인해 보겠습니다.

부동소수점

자바스크립트는 숫자를 저장할 때 64비트 부동소수점을 사용합니다.

😉 프로그래밍을 할 때 64비트 부동소수점을 이용해서 어떻게 저장되는지 자세하게 알 필요는 없습니다.

📌 하지만, 64비트 부동소수점을 저장하기 때문에 발생할 수 있는 오류에 대해서는 반드시 알고있어야 합니다.

• 자바는 0.1+0.2가 0.3이 나옵니다.

  • 자바는 숫자를 변수에 할당할 때 숫자를 위한 별도의 선언자가 있습니다.
  • 예를 들어, int, short, long, double, bigdouble, float, decimal 등이 있습니다.
  • 선언자 자체가 내부적으로 계산의 오류를 미연의 방지하기 위한 코드가 안에 들어가있다고 생각하시면 됩니다.

• 그러나 자바스크립트는 숫자를 담기위한 별도의 선언자 타입이 없습니다.

  • 그래서 0.1+0.2의 값이 0.3이 나오지 않는 일이 발생합니다.
    이게 큰 문제가 되는것인가?를 생각하면, 꼭 그렇지는 않습니다.
  • 왜냐하면, 소수점 이하 10 몇자리를 실생활에서 보여줄 일이 거의 없습니다.
  • 소수점 3, 4자리에서 반올림하는 등의 처리를 해주기 때문입니다.

📌 64비트 부동소수점 저장 원리는 아래와 같습니다.
자바스크립트 숫자 타입의 값이 IEEE 754의 부동소수점 표현 형식 중 배정밀도 64비트 부동소수점 형식을 따릅니다.

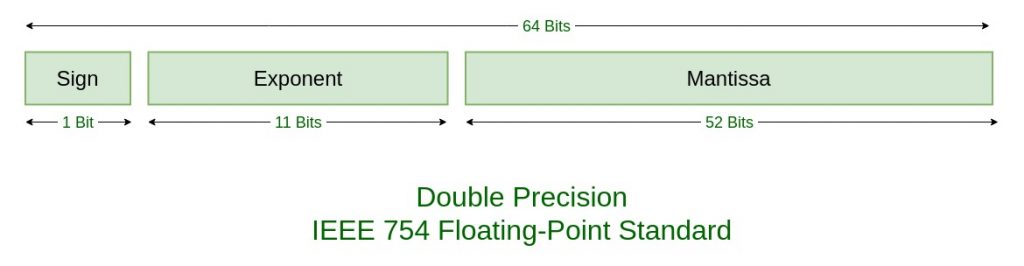
• Sign은 부호부분으로써 양수(0)인지 음수(1)인지를 나타내고 1비트를 사용합니다.
• Exponent는 지수부분으로써 11비트를 차지합니다.
• Mantissa는 가수부분으로써 52비트를 차지합니다.
• 총 64비트로 이루어져 있습니다.
  
  

0.1 + 0.2 === 0.3 ?🤔

0.1 을 부동소수점으로🧐

컴퓨터는 모든 데이터를 2진법을 사용해서 관리합니다.
0.1을 2진수로 나타내면 아래와 같습니다.

console.log(0.1.toString(2));
// 실행결과
0.0001100110011001100110011001100110011001100110011001101

• 부호부분
  • 위에서 첫번째 자리수가 0이니까 부호는 양수입니다.
• 지수부분
  • 지수부분을 어떻게 구하냐면, 2^(n-1)-1+m 이라는 계산원리를 이용합니다.
    • n은 지수부분이 몇비트냐 입니다. 여기서는 11비트니까 n은 11입니다.
    • m은 소수점을 몇번 움직여서 정수값 1이 나왔느냐 입니다.
      0.0001이 1.xxx 가 되려면 소수점을 오른쪽으로 4번 움직입니다. 그래서 m은 -4가 됩니다.
    • 즉, 2^(11-1)-1-4 는 1019가 됩니다.
    • 1019를 2진법으로 나타내면 아래와 같이 10자리가 나옵니다.

    			console.log(1019.toString(2)); //1111111011;

    • 지수부는 11비트를 사용하니까 위의 10자리 맨앞에 0을 추가시켜줘서 01111111011으로 만들어 줍니다.
• 가수부분
  • 아까 0.1을 2진수로 변환한 값에서 소수점을 오른쪽으로 4번 이동 해서 1.100110011001100110011001100110011001100110011001101이 되었습니다.
  • 여기서의 소수점 부분이 가수부분이 됩니다. 총 51자리 수 입니다. 100110011001100110011001100110011001100110011001101
  • 가수부분은 52비트를 쓰니까 여기서는 맨 뒤에 0을 추가시켜주면 1001100110011001100110011001100110011001100110011010 이 됩니다.

최종적으로 0.1의 64비트 부동소수점은 아래와 같습니다.

• 부호부분 0

• 지수부분 01111111011

• 가수부분 1001100110011001100110011001100110011001100110011010

• 최종 부동소수점 표기
  0 01111111011 1001100110011001100110011001100110011001100110011010(2)

• 0.1은 컴퓨터 내부에 위의 부동소수점 값으로 저장됩니다.
  
  

0.2 를 부동소수점으로🧐

0.2도 0.1을 구한것과 같은 방식으로 구해보겠습니다.

console.log(0.2.toString(2));
// 0.001100110011001100110011001100110011001100110011001101

• 부호부분
  • 부호부분의 1비트는 맨 앞의 숫자 0으로써 양수를 나타냅니다.
• 지수부분
  • 지수부분은 위의 공식을 똑같이 대입하면, n은 11, m은 소수점을 오른쪽으로 3번 움직였기때문에 -3이 됩니다. 1.100110011001100110011001100110011001100110011001101
  • 2^(11-1)-1-3 === 1020이 나옵니다. 1020을 2진법으로 나타내면 아래와 같이 10자리가 나옵니다.

  console.log((1020).toString(2)); // 1111111100

  • 맨 앞에 0을 붙여서 최종 지수부분을 01111111100으로 합니다.

• 가수부분
  • 지수부분에서 m 의 값을 구할 때 소수점을 1.100110011001100110011001100110011001100110011001101 으로 만들어줬습니다. 이 값의 소수점 값이 가수부분입니다.
  • 100110011001100110011001100110011001100110011001101는 51자리 이기 때문에 맨뒤에 0을 붙여서 52비트로 만들어줍니다. 1001100110011001100110011001100110011001100110011010

최종적으로 0.2의 부동소수점은

• 0 01111111100 1001100110011001100110011001100110011001100110011010 이 됩니다.
  
  

0.1 + 0.2 ≠ 0.3🧐

부동소수점으로 확인

• 0.1의 부동소수점과 0.2의 부동소수점을 더하면
  0111111110000011001100110011001100110011001100110011001100110100 이 됩니다.

• 하지만, 부동소수점 변환기 링크에 들어가서 0.3의 부동소수점 값을 확인해보면 0011111111010011001100110011001100110011001100110011001100110011 이 나옵니다. 서로 다른 값이 나옵니다.

  console.log(
  `0111111110000011001100110011001100110011001100110011001100110100` 
  ===
  `0011111111010011001100110011001100110011001100110011001100110011`
  ) 
  // false

2진수로 확인

• 0.1과 0.2를 2진수로 바꾸면 소수점 55자리의 2진수가 나옵니다. 그리고 두 값을 더합니다.

  console.log(0.1.toString(2)); // 0.0001100110011001100110011001100110011001100110011001101
  console.log(0.2.toString(2)); // 0.001100110011001100110011001100110011001100110011001101
                           	  //→ 0.0100110011001100110011001100110011001100110011001100111

• 위에서 더한 2진수의 소수점을 없애기 위해서 먼저 10진법으로 바꿔줍니다.

• 10진법으로 표기하기 하기위해 parseInt('2진수', 2)함수를 이용합니다.

• 2진수를 55자리수 만큼 올린 것을 내리기 위해서 1/2의 55승을 곱합니다.

• 최종적으로 아래와 같은 결과가 나오게됩니다.

  
  console.log(parseInt('0100110011001100110011001100110011001100110011001100111', 2) * Math.pow(2, -55)); 
  // 0.30000000000000004

• 2진수로 0.1+0.2 값을 확인해 봐도 0.3이 나오지 않습니다. 0.30000000000000004이 정확한 값이라는 말입니다.

마무리👋

컴퓨터는 숫자를 계산할 때 2진법으로 계산합니다.
몇몇 소수는 10진법에서 2진법으로 변환하는 과정에서 무한 소수가 되어버립니다.
이때 저장공간의 한계가 있는 컴퓨터는 무한 소수를 유한 소수로 바꾸게 됩니다.
이 과정에서 미세한 오차가 발생하면서 값들이 손실되거나 초과하게 됩니다.
이것을 정밀도 문제라고 합니다.
이번에 0.1과 0.2를 더해서 0.3이 나오지 않는 것과 동일한 문제입니다.

소수점 이하 굉장히 깊게 다룰 때, 그리고 굉장히 큰 숫자를 다룰 때는 bignumber.js 같은 오픈소스 라이브러리를 사용합니다.
그렇기 때문에 사실 실무에서는 이런현상 때문에 오류가 발생할 일은 거의 없습니다.

부동소수점을 깊이 있게 알필요는 없습니다.
하지만, 왜 정밀도 문제가 발생하는지를 관심 가지고 계신분들께 가벼운 마음으로 한번은 읽어봤으면 좋겠다는 마음으로 글을 작성하게 되었습니다.

참고

• IEEE 754 부동소수점 변환기
• Why is 0.1 + 0.2 Not Equal to 0.3 in Most Programming Languages?