알고리즘 문제를 풀다가 개념이 명확히 정립되어 있지 않아 공부를 했다.
Longest Increasing Subsequence,
말 그대로 수열 중에서 증가하는 부분이 얼마나 긴지를 구하는데 사용하는 알고리즘이다.
주의할 점은 연속적이지 않아도 된다는 점이다.
[10,20,10,30,20,50] 에서 LIS는 [10,20,30,50]이다.
공통 변수 ⬇️
lst = [10,20,10,30,20,50]DP , O(N^2)
# LIS Algorithm with DP
dp = [1 for _ in range(6)]
for i in range(6):
for j in range(i):
if lst[i] > lst[j]:
dp[i] = max(dp[i],dp[j]+1)
print(max(dp))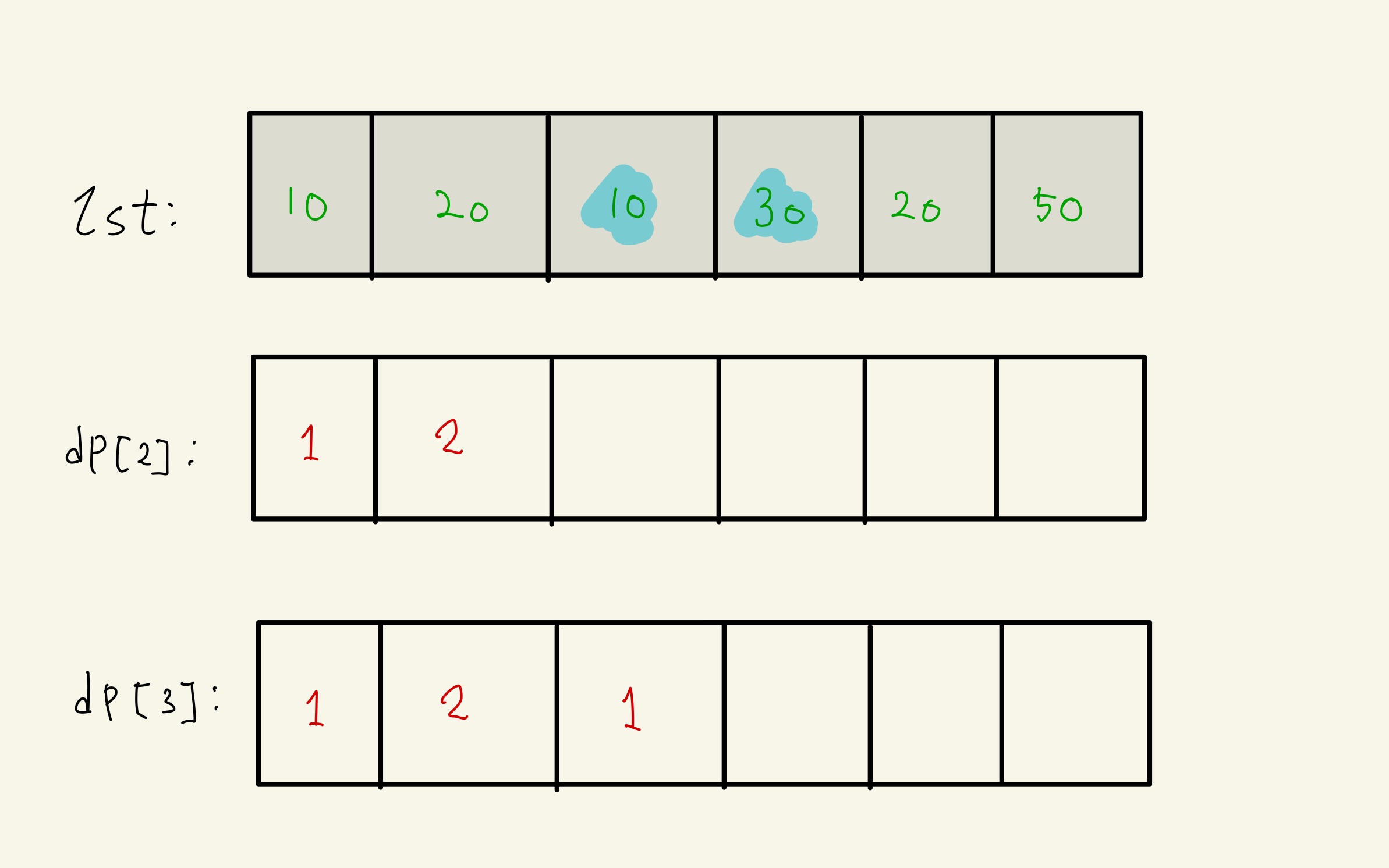
dp[2]와 dp[3]을 구하는 과정을 생각해보자.
리스트에서 2번의 원소는 10이다.
그 이전의 인덱스들(0번,1번)에 대하여 값 비교를 한다.
리스트 0번의 값은 10이다. 10 = 10이므로 증가 수열이 될 수 없다.
리스트 1번은 20이다. 10 < 20이므로 증가 수열이 될 수 없다.
따라서 dp[2]는 초기값 1을 유지한다.
리스트에서 3번의 원소는 30이다.
그 이전의 인덱스들(0,1,2번)에 대하여 값 비교를 한다.
리스트 0번 = 10 < 30이므로 증가 수열이다. 따라서 dp[2]를
기존값 1과 0번에서 1 증가시킨 2 중에서 최대값으로 업데이트를 한다.
따라서 2가 된다.
리스트 1번 = 20 < 30이므로 마찬가지로 증가 수열이다.
똑같이 기존값2와 1번에서 1 증가시킨 3중에서 최대값 업데이트를 한다.
이렇게 최종적으로 dp[3]은 3이 된다.
이 과정을 끝까지 반복하면 dp[5]에서 4가 나오고 dp 중에서 해당 값이 제일 크므로 이것이 LIS의 길이다.
Binary Search , O(NlogN)
# LIS Algorithm with Binary Search
from bisect import bisect_left
dp = [lst[0]]
for i in range(6):
if lst[i] > dp[-1]:
dp.append(lst[i])
else:
idx = bisect_left(dp,lst[i])
dp[idx] = lst[i]
print(len(dp))DP를 이용하는 방법은 O(N^2)의 시간복잡도다.
만약 입력 제한 조건이 많아진다면 시간 초과를 면하기 힘들다.
이 때, 사용할 수 있는 방법이 이분탐색이다.
bisect.bisect_left(lst,x): list에서 x가 들어갈 인덱스 반환. 단, list가 오름차순 정렬되어 있어야 함.
리스트를 순회하며 현재 원소가 이전 원소보다 크다면 증가수열이므로 dp에 추가
작거나 같다면 증가수열이 아니므로 dp에 추가시키진 않는데,
우리는 최대한 긴 증가수열을 찾는 것이 목적이므로 증가수열의 밀집도가 최대한 오밀조밀해야 가장 길게 나온다.
예를 들어, [2,1,3,5,4,...] 리스트에서
[1,3,5]보다는 [1,3,4]로 dp 배열을 만들어 나가야지 뒤에 나올 원소들에 대하여 더욱 높은 밀집도를 가질 수 있기 때문이다.
아직 명쾌하게 설명이 안 되는 것을 보니, 이해가 깊게 되지 않았나 보다. 나중에 내공을 더 쌓고 돌아오도록 하겠다. 🙏🏻
이분탐색은 O(logN)의 시간복잡도이므로 dp 반복문까지 합치면
최종적으로 O(NlogN)의 시간복잡도가 나온다.

잘 보고갑니다 ㅎㅎ