본 포스팅은 플레이데이터 알고리즘 스터디 멘토링 자료입니다.

서론

BFS는 weight가 없는 그래프에서 특정 노드에서 특정 노드까지의 최단 거리를 구하는데 사용한다.

여기서 핵심은 최단거리 다.

지금부터 설명할 모든 내용은 맨 위 구문을 이해하기 위함이다.

따라서, 아직 BFS가 와닿지 않는 사람들은 그냥 "BFS는 최단거리를 구할때 사용한다." 라고 이해하고 있으면 될 것 같다.

그래프

먼저 BFS를 논하기 전에 그래프라는 개념부터 알아야 한다.

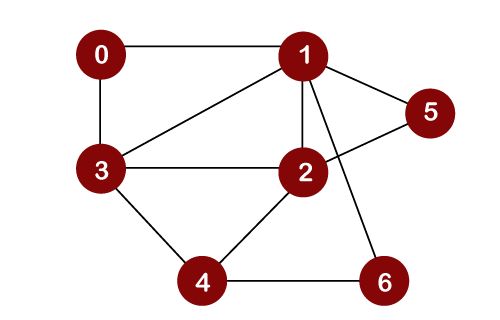
위 그림이 그래프다.

0,1,2,...,6 동그라미를 [정점] 영어로는 [노드] 혹은 [버텍스] 라고 칭한다.

그리고 이를 연결하는 선들을 [간선] 영어로는 [엣지]라고 한다.

이 포스팅에서는 노드와 간선으로 설명하겠다.

0번 노드에서 6번 노드까지의 최단거리가 어떻게 될까?

여러 경로가 있지만 0->1->6으로 2가 가장 짧은 거리다.

만약 bfs(start,end)라고 함수를 정의한다면

위 그래프에서 bfs(0,6)은 2를 반환한다.

그렇다면 아래 그래프를 보자.

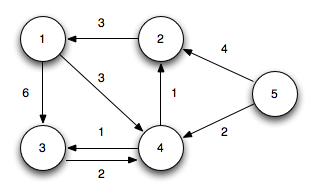
5번 노드에서 2번노드까지의 최단거리는 어떻게 될까?

5->4->2로 2+1 = 3다.

이것도 bfs(5,2) 하면 3이 나올까?

결론적으로 말하면 아니다. 위에서 잠깐 언급하였듯이 BFS는 weight가 없는 그래프에서만 적용된다. 여기서 weight란 간선의 비용을 의미한다.

화살표의 개수로만 따지면 5->2로 제일 짧아보이지만 비용이 4이므로 이는 최단거리가 아니다.

이처럼 weight가 있는 그래프에서의 최단거리는 다익스트라 알고리즘을 사용한다. 여기서는 몰라도 되니 패스

생성 방법

먼저 이 그래프를 파이썬 코드로 표현해보겠다.

# Make Graph
from collections import defaultdict
N,M = map(int,input().split())
graph = defaultdict(list)

for i in range(M): 
    m,k = map(int,input().split())
    graph[m].append(k)
    graph[k].append(m)

테스트

위에서 만든 그래프로 BFS 테스트를 해보겠다.

코드 내용은 아직 이해를 못해도 좋다.

본인이 구하고 싶은 최단거리가 잘 나오는지 확인해보자.

from collections import deque
def bfs(graph,s,t):
    q = deque([(s,0)])
    visited = [False]*len(graph)
    visited[s] = True
    while q:
        cur,cnt = q.popleft()

        if cur == t:
            return cnt
        
        for nxt in graph[cur]:
            if not visited[nxt]:
                q.append((nxt,cnt+1))
                visited[nxt] = True
    return -1

BFS

그림 설명

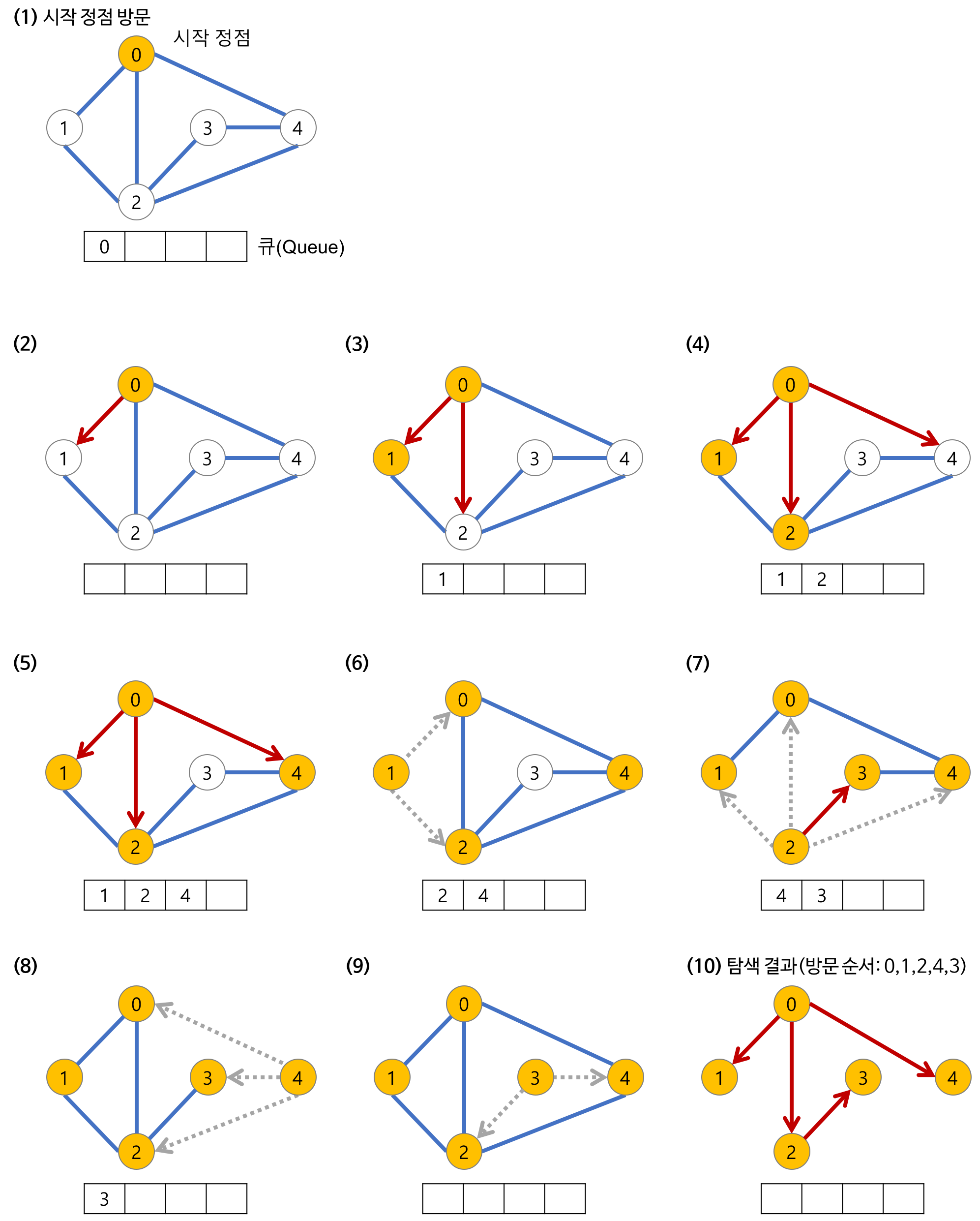
0번 노드에서 3번 노드로 가는 최단거리를 구해보겠다.

큐에 다음 방문할 노드를 삽입하고 순차적으로 꺼내며 탐색한다.

1. 0번이 시작이니까 0을 큐에 넣는다.

2. 3. 4. 0번을 꺼내고 이 노드와 연결된 노드들(1,2,4) 중에서 방문하지 않은 노드들(1,2,4)을 큐에 넣는다.

3. 1번을 꺼내고 이 노드와 연결된 노드들(0,2) 중에서 방문하지 않은 노드들(없음)을 큐에 넣는다.

👉🏻 0번과 2번이랑 연결되어 있지만 이미 큐에 들어간 적이 있으므로 방문 처리를 하여 큐에 넣지 않는다.

6. 7. 8. ... 위 과정을 반복한다.

그래프를 완전 탐색할 때는 10번까지 이어지지만 우리는 3번 노드까지의 거리를 알고 싶은 것이기 때문에 9번에서 종료하고 거리를 반환한다.

코드 이해

q = deque([(s,0)])

시작 지점 s를 큐에 넣는다. 이 때, 파라미터로 0을 추가해주는 이유는 현재까지의 거리를 알기 위해서다.

예) (4,3): 현재 4번 노드에 위치해 있고 시작 지점으로부터 거리는 3이다.

(s,0)은 현재 s 노드에 위치해 있고 s에서부터 s까지의 거리는 0이라는 뜻이다.

visited = [False]*len(graph)

방문여부를 확인하기 위한 리스트다.

False는 아직 방문하지 않음. True는 방문했다는 뜻이다.

예를 들어, visited[1] = True 이면 1번 노드를 방문했다는 의미.

visited[s] = True

s 노드 방문 처리

while q:
	if cur == t:
    	return cnt
return -1

큐가 빌 때까지 반복해서 탐색하다가 현재 지점이 타겟 노드면 현재까지 이동한 거리(cnt)를 반환한다.

큐가 다 빌 때까지 못 찾았다면 s ➡️ t 의 경로가 없는 것이니 -1을 반환.

cur,cnt = q.popleft()

현재 노드와 이동 횟수(거리)를 꺼낸다.

for nxt in graph[cur]:
            if not visited[nxt]:
                q.append((nxt,cnt+1))
                visited[nxt] = True

현재 노드와 연결되어 있는 노드들 중에서
방문하지 않은 노드라면
큐에 노드를 추가하고
해당 노드를 방문처리 한다.

예제 문제

https://school.programmers.co.kr/learn/courses/30/lessons/1844

(해설)

숙제

• 예제 문제를 해설보지 않고 내 손으로 다시 풀어보기.

Reference

https://hsp1116.tistory.com/42
https://www.javatpoint.com/bfs-vs-dfs
https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html