[ADsP 합격 노트] 3-3. 통계 분석

통계분석의 이해

• 표본 추출 방법

  • 단순랜덤 추출법(simple random sampling)
  • 계통 추출법(systematic sampling) (e.g. 5개마다 조사)
  • 집락 추출법(cluster random sampling) (e.g. 지역표본추출, 다단계표본추출)
  • 층화추출법(stratified random smapling)

• 표본조사

  • 표본오차(sampling error) : 모집단을 대표할 수 있는 표본 단위들이 조사대상으로 추출되지 못함으로서 발생하는 오차
  • 비표본 오차 : 표본오차를 제외한 모든 오차로서 조사 과정에서 발생하는 모든 부주의나 실수, 알 수 없는 원인 등 모든 오차를 의미하며 조사대상이 증가하면 오차가 커진다.
  • 표본편의(sampling bias) : 모수를 작게 또는 크게 할 때 추정하는 것과 같이 표본추출방법에서 기인하는 오차
    • 표본추출 과정에서 특정 대상이 다른 대상에 비해 우선적으로 추출될 때 생기는 오차
    • 표본편의는 확률화(randomization)에 의해 최소화하거나 없앨 수 있다.
  • 확률 표본(random sample) : 모집단으로부터 편의되지 않은 표본을 추출하는 절차(확률화)에 의해 추출된 표본

• 측정 방법

  • 질적척도
    • 명목척도 : 어느 집단에 속하는지
    • 순서척도 : 서열관계
  • 양적척도
    • 구간척도 : 구간이나 구간 사이의 간격이 의미가 있는 자료 (온도, 지수)
      *곱하기, 나누기는 불가능
    • 비율척도 : 절대적 기준인 0이 존재하고 사칙연산이 가능 (무게, 나이, 시간, 거리)

• 통계분석

  • 기술통계
  • 통계적 추론(추측통계) : 모수 추정, 가설검정, 예측

• 확률

  • 표본공간($\Omega$) : 어떤 실험을 실시할 때 나타날 수 있는 모든 결과들의 집합
  • 확률 $P(E) = \frac{n(E)}{n(\Omega)}$
    
  • 확률 변수 : 정의역이 표본공간, 치역이 실수값(0<y<1)인 함수
  • 덧셈정리
    • 배반이 아닐 때 : $P(A\bigcup B)=P(A)+P(B)-P(A\bigcap B)$
    • 배반일 때 : $P(A\bigcup B)=P(A)+P(B)$
  • 곱셈정리 : 독립사건일때 A와 B가 동시에 나타날 확률 $P(A\bigcap B)=P(A)*P(B)$
    

• 확률 분포

  1) 이산형 확률 변수

  이산형 확률 분포	설명	예시
  베르누이 확률 분포	결과가 2개만 나오는 경우	안타를 칠 확률
  이항분포	베르누이 시행을 n번 반복했을때 k번 성공할 확률 - n이 충분히 크면 정규분포에 가까워짐	경기에서 5번 타석에 틀어와서 3번 안타를 칠 확률은 이항분포를 따른다.
  기하분포 (초기하분포)	성공확률이 p인 베르누이 시행에서 첫번째 성공이 있기까지 x번 실패할 확률	경기에서 5번 타석에 들어와서 3번째 타석에서 안타를 칠 확률은 기하분포를 따른다(장기하의 첫 번째 성공..)
  다항분포	세 가지 이상의 결과를 가지는 반복시행
  포아송 분포	시간과 공간 내에서 발생하는 사건의 발생횟수에 대한 확률분포	추신수선수가 최근 5경기에서 10개 홈런을 때렸다. 오늘 경기에서 홈런을 못 칠 확률은 포아송분포를 따른다.

  2) 연속형 확률 변수

  연속형 확률 분포	설명
  균일 분포
  정규 분포	평균이 $\mu$이고, 표준편차가 $\sigma$인 $x$의 확률밀도함수
  지수 분포	어떤 사건이 발생할 때까지 경과 시간에 대한 연속확률분포
  t-분포	평균이 0을 중심으로 좌우가 동일한 분포 - 자유도가 증가하면 표준정규분포와 같아짐 - 두 집단의 평균이 동일한지 알고자 할 때 검정통계량으로 활용
  $x^2$-분포(카이제곱)	- 모평균과 모분산이 알려지지 않은 모집단의 모분산에 대한 가설 검정에 사용 - 정규모집단으로부터 n개의 단순임의추출한 표본의 분산은 자유도 n-1인 카이제곱분포를 따른다 - 두 집단 간의 동질성 검정에 활용
  F-분포	- 두 집단간 분산의 동일성 검정에 사용 - 자유도 2개

  ★ 정규분포를 표준정규분포로 만들기 위한 식?

  $Z=\frac{X-\mu}{\sigma}$
  

• 추정

  1) 점추정

  • 점추정량의 조건
    - 불편성 : 표본에서 얻은 추정량의 기댓값은 모집단의 모수와 편의가 없다.
    - 효율성 : 추정량의 분산이 작을 수록 좋다
    - 일치성 : 표본의 크기가 아주 커지면, 추정량이 모수와 거의 같아진다.
    - 충족성 : 추정량은 모수에 대해 모든 정보를 제공한다

    2) 구간추정

  • 95% 신뢰수준 하에서 모평균의 신뢰 구간

    • 모분산이 알려져 있는 경우

      $(\bar X-1.96\frac{\sigma}{\sqrt{n}}, \bar X+1.96\frac{\sigma}{\sqrt{n}})$

      표준정규분포 $N(0,1)$을 따르는 $Z=\frac{X-\mu}{\sigma/\sqrt{n}}$ 통계량 이용
      

    • 모분산이 알려져 있지 않은경우, 표본분산을 사용

      $(\bar X-2.26\frac{S}{\sqrt{n}}, \bar X+2.26\frac{S}{\sqrt{n}})$

      자유도가 n-1인 t-분포를 따르는 $T=\frac{X-\mu}{S/\sqrt{n}}$ 통계량 이용

      *신뢰수준 95% : 모수가 신뢰구간 내에 존재할 확률이 95%라는 의미

• 가설검정
  • 유의수준($\alpha$) : 귀무가설이 옳은데도 이를 기각하는 확률의 크기
  • 제1종 오류($\alpha$) : $H_0$가 사실인데도, 사실이 아니라고 판정(귀무가설 기각)
    • p-value : 귀무가설이 사실인데도 불구하고 사실이 아니라고 판정할 때 실제 확률을 의미
  • 제2종 오류($\beta$) : $H_0$가 사실이 아닌데도, 사실이라고 판정(귀무가설 채택)
• 비모수검정
  • 주로 명목형 변수? 관측된 자료가 많지 않거나 자료가 서열관계를 나타내는 경우
  • 자료가 추출된 모집단의 분포에대한 아무 제약을 가하지 않고 검정 실시
  • 가정된 분포가 없으므로 가설은 단지 ‘분포의 형태가 동일하다’와 같이 설정
  • 관측값들의 순위나 두 관측값 차이의 부호등을 이용해 검증
  • 비모수검정의 예
    • 부호검정, 윌콕슨의 순위합검정, 윌콕슨의 부호순위합검정, 만-위트니의 U검정, 스피어만의 순위상관계수

기초 통계분석

• 왜도 : 양수이면 오른쪽으로 긴 꼬리 (순서: 최빈값 → 중앙값 → 평균)
• 첨도 : 양수이면 표준정규분포보다 더 뾰족함
• 막대그래프 : 범주형으로 구분된 데이터를 표현, 범주의 순서를 의도에 따라 바꿀 수 있음
• 히스토그램 : 연속형 데이터를 표현,임의로 순서를 바꿀 수 없고 막대의 간격이 없음
  • 계급의 수 : $2^k ≥ n$을 만족하는 최소의 정수(k)
  • 표본의 크기가 작으면 각 막대의 높이가 데이터 분포의 형상을 잘 표현해내지 못함
  • 봉우리가 여러개 있는 데이터는 일반적으로 2개 이상의 공정이나 조건에서 데이터가 수집되는 경우 발생
• 파레토 그림(pareto diagram)은 명목형 자료에서 “중요한 소수”를 찾는데 유용한 방법
• 공분산: $Cov(X, Y) = E[(X-\mu_X)(Y-\mu_Y)]$
  • 공분산의 부호가 + 이면 두 변수는 양의 방향성을 가진다
  • X, Y가 서로 독립이면, 공분산은 0이다.
• 상관분석

  • 상관분석의 유형 : 피어슨/스피어만

    ★ 스피어만, 서열척도, 순서, 순위상관게수 등의 단어는 다 “ㅅ”으로 시작함

    • 스피어만 상관계수 : 비선형적 상관관계 나타낼 수 있음

  • t 검정통계량을 통해 얻은 p-value 값이 0.05이하인 경우, 대립가설을 채택하게 되어 우리가 데이터를 통해 구한 상관계수를 활용할 수 있음

    data(mtcars)
    a <- mtcars$mpg
    b <- mtcar$hp
    cor(a,b)
    cov(a,b)
    cor.test(a, b, method="pearson") 

회귀분석

• 회귀분석 정의: 하나나 그 이상의 독립변수들이 종속변수에 미치는 영향을 추정할 수 있는 통계 기법
• 회귀분석의 변수
  • y : 반응변수, 종속변수, 결과변수
  • x : 설명변수, 독립변수, 예측변수
• 선형회귀분석의 가정(★)
  • 선형성
  • 등분산성($\neq$이분산성) : 오차(항)의 분산이 입력변수와 무관하게 일정하다
  • 독립성 : 입력변수와 오차(항)는 관련이 없다.
  • 비상관성 : 오차(항)들끼리 상관이 없다
  • 정상성(정규성) : 오차(항)의 분포가 정규분포를 따른다.
    • 히스토그램, Q-Q plot, Kolmogolov-Smirnov검정, Shaprio-Wilk검정, Anderson-Darling Test 등

1. 단순선형회귀분석

   • 회귀분석에서의 검토 사항

     • 회귀계수들이 유의미한가? → p-value<0.05
     • 모형이 얼마나 설명력을 갖는가? → 결정계수($R^2$) (0~1)
     • 모형이 데이터를 잘 적합하고 있는가? → 잔차 그래프

   • 회귀계수의 추정 : 잔차제곱이 가장 적은 선을 구하는 것

     • 회귀계수 추정량 : “최소제곱”

   • 결정계수($R^2$) : 총 변동 중에서 회귀 모형에 의해 설명되는 변동이 차지하는 비율

     • 오차: 모집단에서 실제값이 회귀선과 비교해볼때 나타나는 차이
     • 잔차 : 표본에서 나온 관측값이 회귀선과 비교해볼 때 나타나는 차이

     

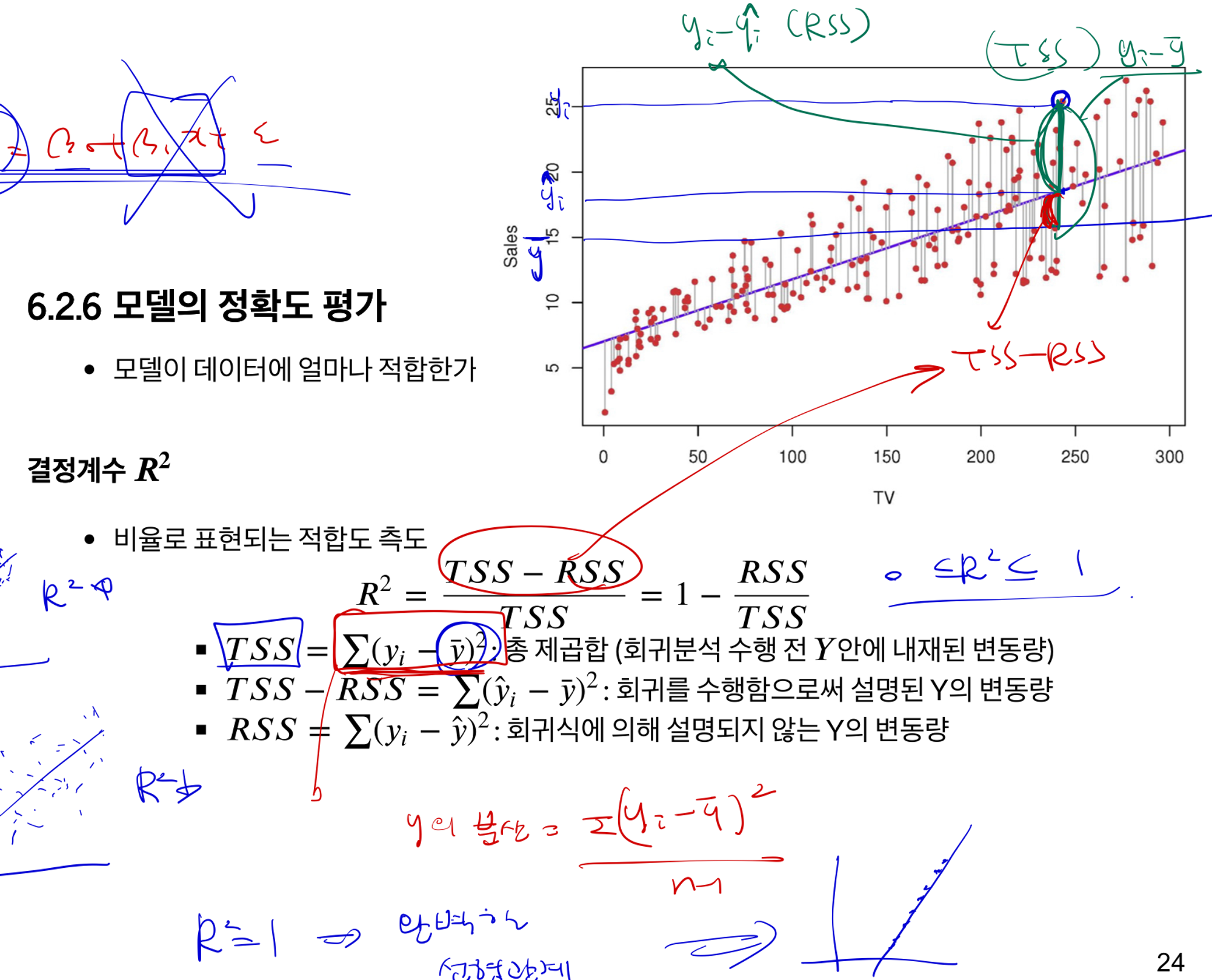
     표본평균보다 내 모델이 확실히 $y$를 더 많이 설명한다고 할 수 있냐?

     • 예제 (결정계수 $R^2$ 계산)

       

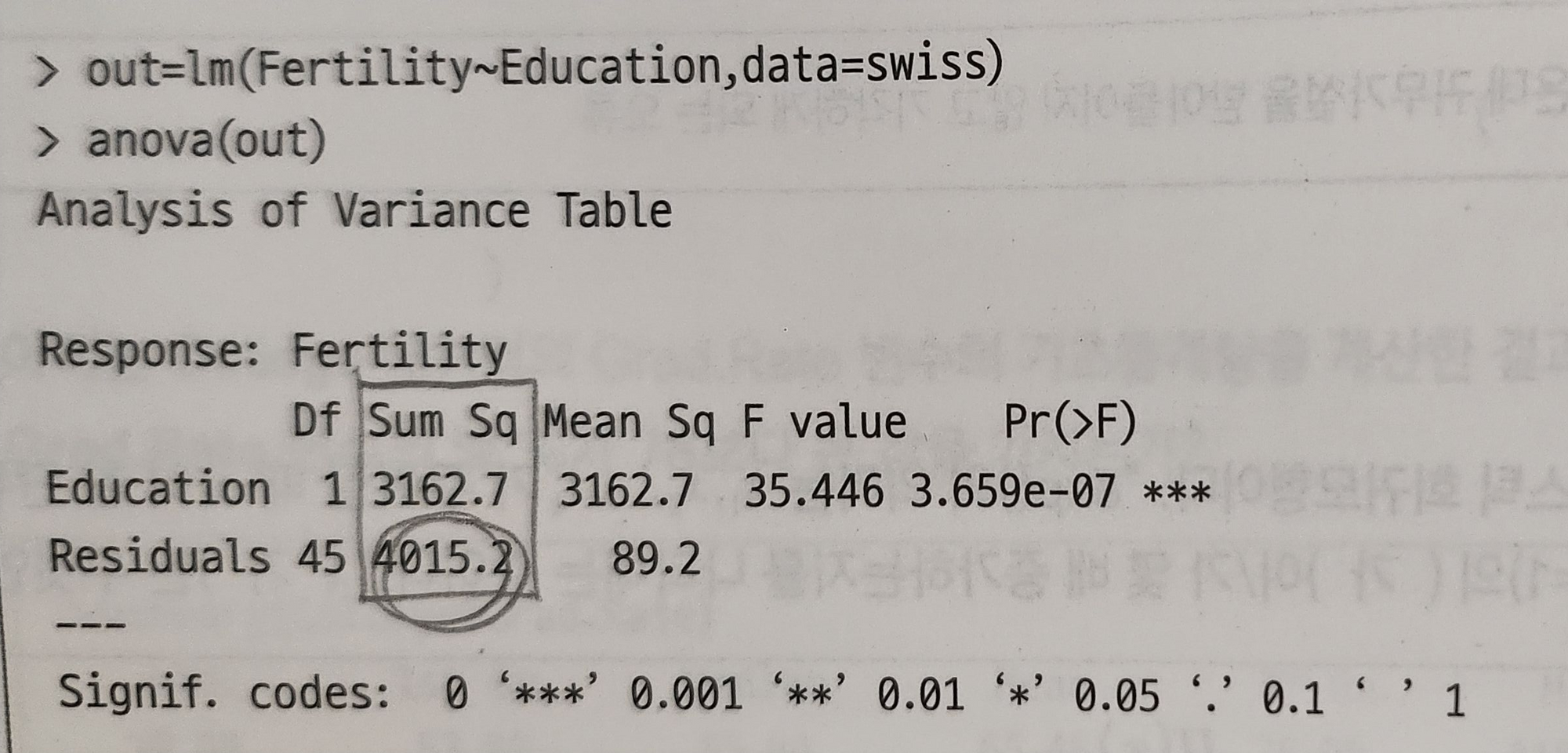
       Sum of square(TSS) = 3162.7 + 4015.2 = 7178

       RSS = 4015.2

       $R^2=1 - \frac{4015.2}{7178} = 0.441$
       

   • 회귀직선의 적합도 검토
     • 다변량 회귀분석에서는 독립변수가 유의하든, 유의하지 않든 독립변수의 수가 많아지면 결정계수($R^2$)가 높아지는 단점이 있다.
     • 이러한 결정계수의 단점을 보완하기 위해 수정된 결정계수($R^2_a$)를 활용. 결정계수보다 작은 값으로 산출되는 특징이 있음

2. 다중선형회귀분석

   • 모형의 통계적 유의성
     • F통계량으로 확인
     • 유의수준 5% 하에서 F통계량의 p값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의하다고 볼 수 있다.
   • 다중공선성 : 다중회귀분석에서 설명변수들 사이에 선형관계가 존재하면 회귀계수의 정확한 추정이 곤란
     • 다중공선성 검사방법
       • 분산팽창요인(VIF) : 4보다 크면 다중공선성이 존재한다고 봄. 10보다 크면 심각한 문제.
       • 상태지수 : 10이상이면 문제 있음, 30보다 크면 심각한 문제
     • 다중선형회귀분석에서 다중공선성의 문제가 발생하면, 문제가 있는 변수를 제거하거나 주성분회귀, 능형회귀 모형을 적용하여 문제를 해결한다
   • 회귀분석의 종류
     • 단순회귀, 다중회귀
     • 로지스틱 회귀

       data(nodal) 
       glmModel <- glm(r~., data=data, family="binomal")
       summary(glmModel) 

     • 다항회귀 ($X_1, X_2, X^2_1, X_1X_2)$
     • 곡선회귀($X, X^2$)
     • 비선형회귀($Y=e^{-\beta X}+\epsilon$)

3. 최적회귀방정식

   • 전진선택법
   • 후진제거법

   → 두 모델 결과가 다를 수 있음

   • 단계선택법(단계적 방법) : 전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수의 중요도가 약화되면 해당변수를 제거하는 등 단계별로 추가 또는 제거되는 변수의 여부를 검토
   • 벌점화된 선택 기준 : 모형의 복잡도에 벌점을 주는 방법 (AIC, BIC)

     • 모든 후보 모형들에 대해 AIC 또는 BIC를 계산하고 그 값이 최소가 되는 모형을 선택

       ##### 전진선택법
       # step(lm(출력변수~입력변수, 데이터세트), scope=list(lower=~1, upper=~입력변수), 
       #			direction="변수선택방법")
       # (k =2) AIC, (k=log(자료의 수)) BIC 
       step(lm(y~1, data=df), scope=list(lower=~1, upper=~x1+x2+x3+x4), direction="foward")