[3주차1일차] Chapter 03_기초수학 기초7

조합

조합이란?

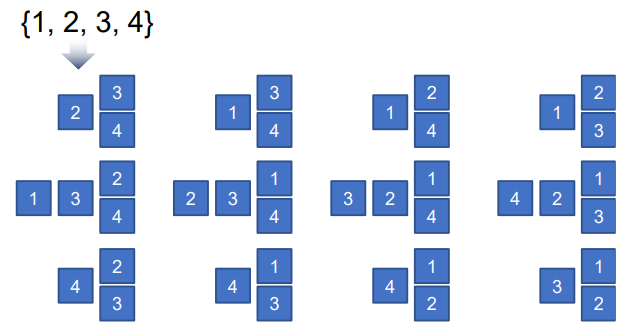
n개에서 r개를 택하는 경우의 수

4개에서 3개를 택하는 경우

순열과 조합

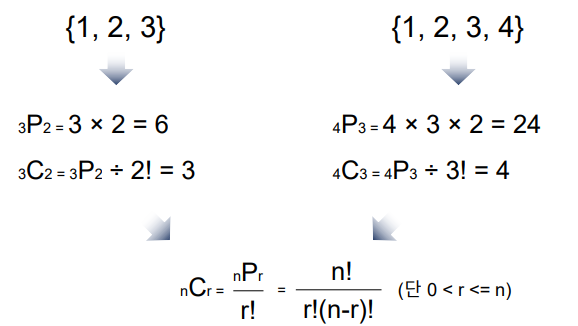
조합 (파이썬)

조합

파이썬을 이용해서 다음 조합들의 값을 구하는 프로그램 만들기

numN = int(input('numN 입력: '))
numR = int(input('numR 입력: '))
resultP = 1
resultR = 1
resultC = 1

for n in range(numN, (numN-numR), -1):
    print('n : {}' .format(n))
    resultP = resultP * n

print('resultP: {}' .format(resultP))

for n in range(numR, 0, -1):
    print('n : {}' .format(n))
    resultR = resultR * n

print('resultR: {}' .format(resultR))

resultC = int(resultP / resultR)
print('resultC: {}' .format(resultC))

확률

확률이란?

모든 사건에서 특정 사건이 일어날 수 있는 수를 나타낸 것
[동전]

• 모든 사건: 앞, 뒤 -> 2가지 경우
• 특정 사건: 앞->1가지 경우, 뒤->1가지 경우
• 확률: 앞->1/2, 뒤->1/2
  [주사위]
• 모든 사건: 1, 2, 3, 4, 5, 6 -> 6가지 경우
• 특정 사건: 1->1가지 경우, 2->1가지 경우, 3->1가지 경우, 4->1가지 경우, ...
• 확률: 1->1/6, 2->1/6, 3->1/6, 4->1/6, 5->1/6, 6->1/6

모든 사건 => 표본 공간

특정 사건 => 사건

확률과 조합

조합을 이용해서 확률을 알아낼 수 있다.
[뽑기]
박스에 '꽝'이 적힌 종이가 4장이 있고, '선물'이 적힌 종이가 3장이 있다. 3장을 뽑을 경우 다음 경우의 수를 구해보자.

확률 (파이썬)

확률

박스에 '꽝'이 적힌 종이가 4장이 있고, '선물'이 적힌 종이가 3장이 있을 때, 파이썬을 이용해서 '꽝' 2장과 '선물' 1장을 뽑는 확률(%)을 출력하자.

# 확률 구하기 위해 함수 이용하기
def proFun():
    numN = int(input('numN 입력: '))
    numR = int(input('numR 입력: '))

    resultP = 1
    resultR = 1
    resultC = 1

    #순열 구하기
    for n in range(numN, (numN - numR), -1):
        resultP = resultP * n
    print('resultP: {}' .format(resultP))

    #조합공식(nPr / r!)에서 r!구하기
    for n in range(numR, 0, -1):
        resultR = resultR * n
    print('resultR: {}' .format(resultR))

    #조합구하기 - 조합공식(nPr / r!)
    resultC = int(resultP / resultR)
    print('resultC: {}' .format(resultC))

    return resultC

sample = proFun()
print('sample: {}' .format(sample))

event1 = proFun()
print('event1: {}' .format(event1))

event2 = proFun()
print('event2: {}' .format(event2))

probability = (event1 * event2) / sample
print('probability: {}%' .format(round(probability * 100, 2)))