CS229 Machine Learning (2018 Autumn 2주차)

이론

용어 정의

$m$ : dataset 개수

$n$ : input 차원, feature 개수

$X$ : input (주로 vector)

$y$ : output (주로 scalar)

$(X^{(i)}, y^{(i)})$ : i번째 dataset

$X_j$ : input의 j번째 feature

scalar : 0차원 값

vector : 1차원 배열

matrix : 2차원 배열

Dataset 예시

$X$	$X$	...	$X$	$y$
$x^{(1)}_1$	$x^{(1)}_2$	...	$x^{(1)}_n$	$y^{(1)}$
$x^{(2)}_1$	$x^{(2)}_2$	...	$x^{(2)}_n$	$y^{(2)}$
...	...	...	...
$x^{(m)}_1$	$x^{(m)}_2$	...	$x^{(m)}_n$	$y^{(m)}$

Gradient Descent

$J(\theta)$를 최소화하기 위해 $J(\theta)$가 감소하는 방향으로 $\theta$를 업데이트한다.

선형 회귀 학습 방법

Batch Gradient Descent Linear Regression

매 학습 단계마다 모든 training set을 보고 $\cfrac{dJ(\theta)}{d\theta}$를 구해 $\theta$를 업데이트한다.

학습 속도가 느리지만, 결국 $\theta$가 $J(\theta)$를 최솟값으로 만드는 값으로 수렴한다.

Stochastic Gradient Descent Linear Regression

매 학습 단계마다 1개의 training set을 보고 $\cfrac{dJ(\theta)}{d\theta}$를 구해 $\theta$를 업데이트한다.

학습 속도가 빠르지만, $\theta$가 수렴하지 않고 특정 범위 안에서 진동한다. 이 경우 매 학습 단계마다 학습률을 줄이면 $\theta$가 특정 값에 수렴한다. 하지만 이 수렴된 값이 최적의 $\theta$값은 아니다.

Mini-Batch Gradient Descent Linear Regression

매 학습 단계마다 n개의 training set을 보고 $\cfrac{dJ(\theta)}{d\theta}$를 구해 $\theta$를 업데이트한다.

n값에 따라 Batch와 Stochastic의 중간 장단점을 가진다.

혼합

초반엔 Stochastic으로 하다 후반엔 Batch로 학습시키기

Normal Equation

$J(\theta)$를 최소화하는 $\theta$는 $\cfrac{dJ(\theta)}{d\theta} = 0$ 이라는 점을 이용해, 각 $\theta_j$에 대해 연립 방정식을 세워서 풀면 $\theta$를 한번에 찾을 수 있다.

예시

배치 경사하강 선형 회귀

Forwarding

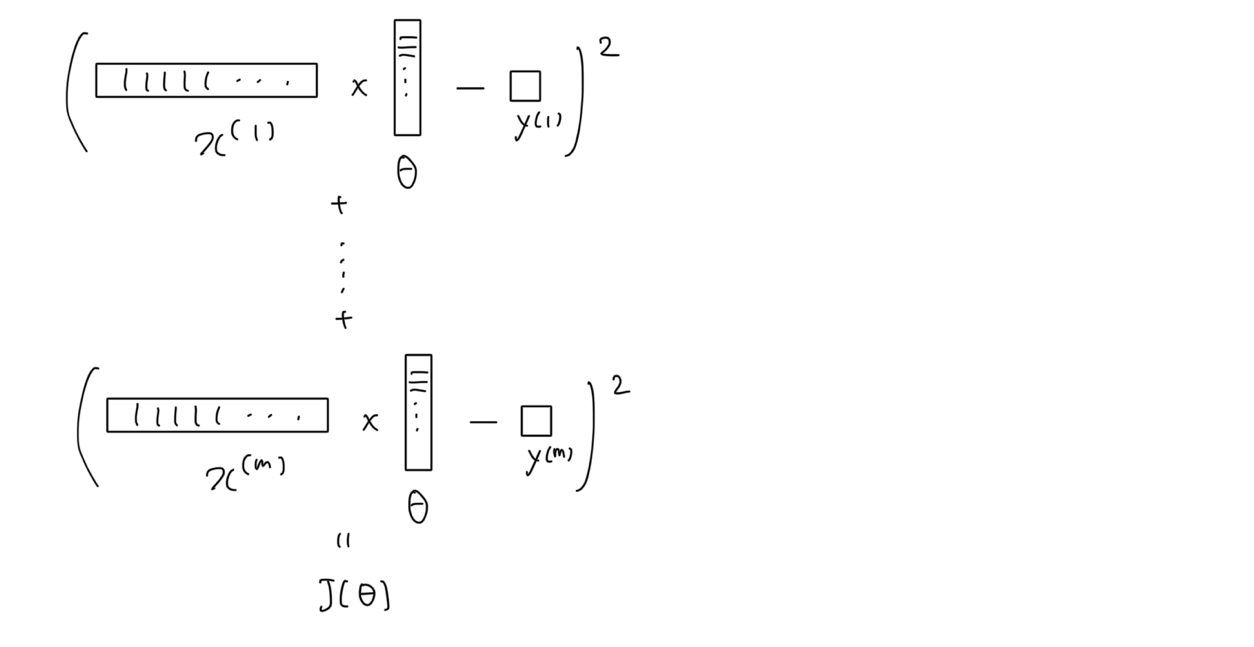
오차를 구하는 과정

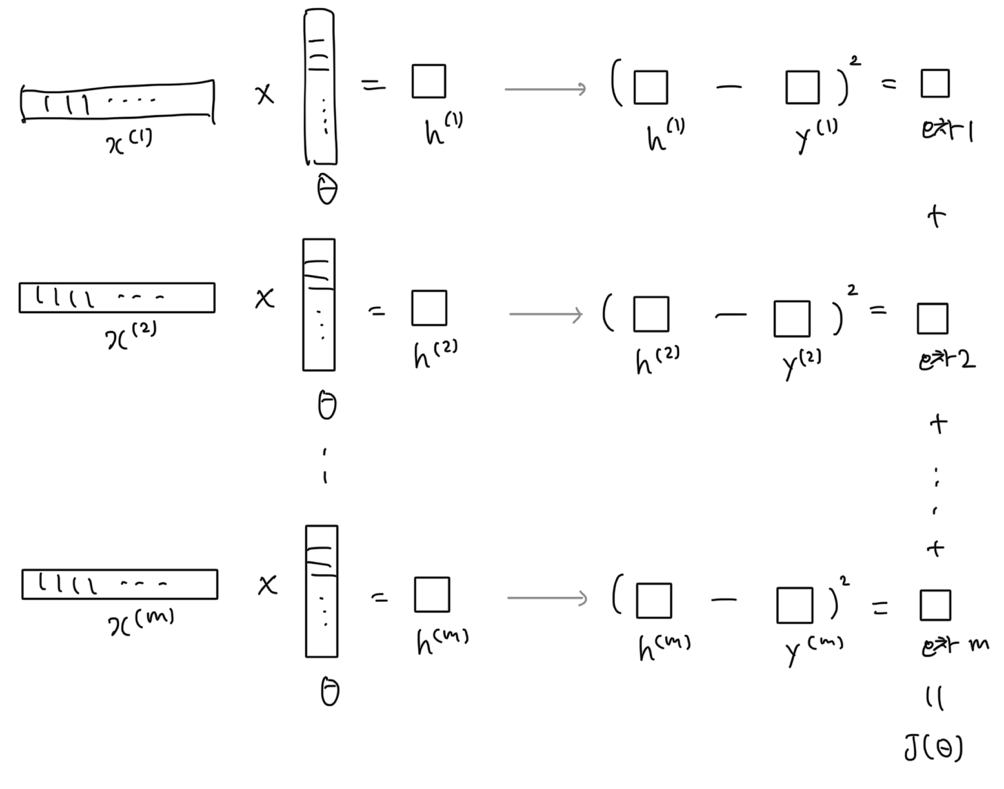
오차를 구하는 자세한 과정

Back Propagation

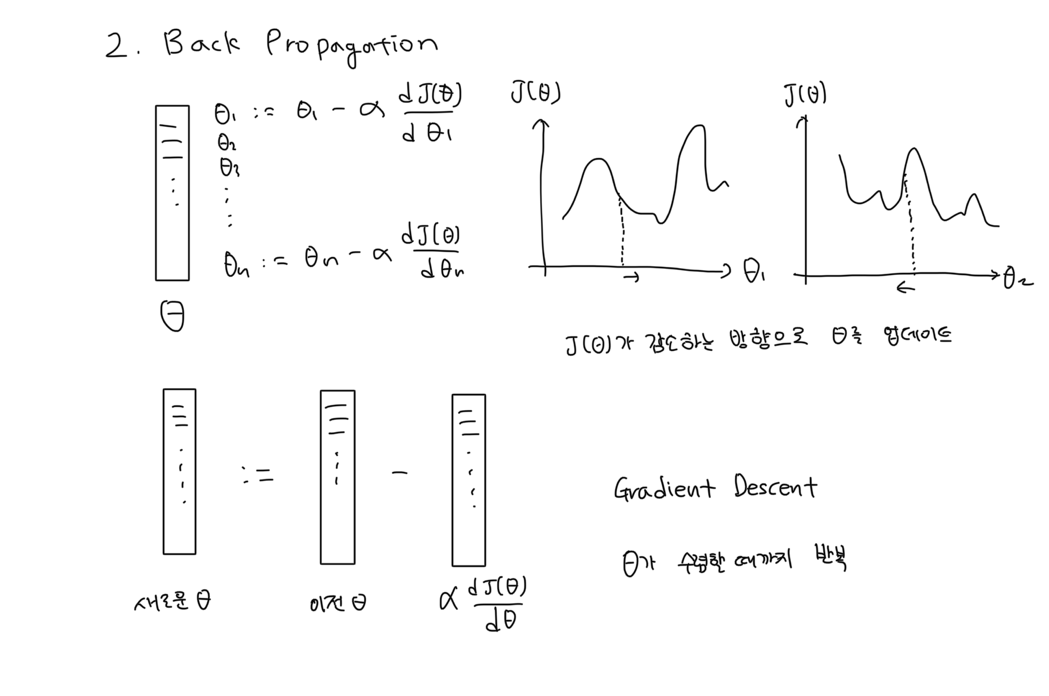
$\theta_j$의 절댓값이 0~1이면 일반적으로 학습률을 0.01로 잡고 기하급수적으로 늘려서 적절한 학습률 값을 찾는다. 만약 $\theta$를 업데이트했는데 $J(\theta)$가 증가하면 학습률이 크다는 뜻이다.

여기서 $J(\theta)$는 (위 그림과 달리) $\theta$에 대한 2차 함수여서 convex하기 때문에 항상 전역 최소점이 존재하고, 전역 최소점 = 지역 최소점이다.

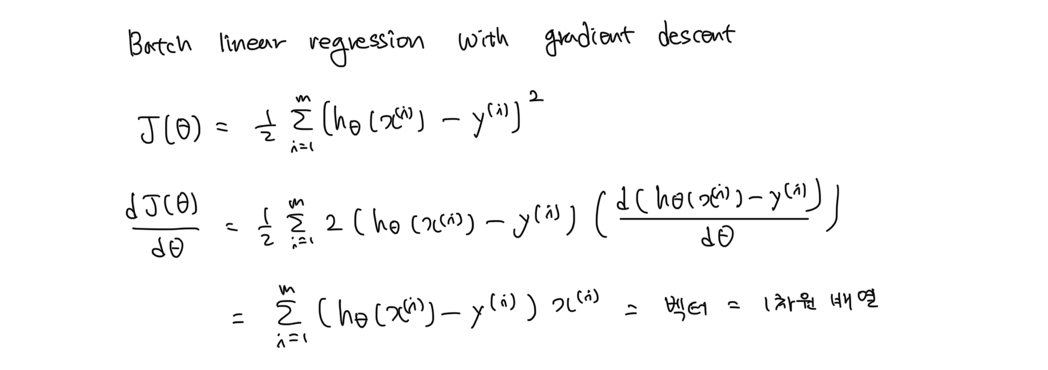
$\cfrac{dJ(\theta)}{d\theta}$ 는 위 그림과 같이 구할 수 있다.

정규 방정식 선형 회귀

$\theta = (X^TX)^{-1}X^TY$

위 공식을 활용하면 $\theta$ 값을 한번에 구할 수 있다. 선형 회귀만 $\theta$ 값을 한번에 구할 수 있는 공식이 존재한다.