
행렬을 가우스 행렬 형태로 변환하여 방정식의 해를 구하는 방법 = 가우스 소거법
행렬을 기약 가우스 행렬 형태로 변환하여 방정식의 해를 구하는 방법 = 가우스 조르단 소거법
가우스 소거법과 가우스 조르단 소거법은 선형시스템을 따르는 행렬식에서 해를 구할 때 사용되는 방법이다.
서로 연관되는 개념은 다음과 같다.
기약 행 사다리꼴(RREF Reduced Row Echelon Form) <-> 행 사다리꼴(Row Echelon Form)
기약 가우스 행렬 <-> 가우스 행렬
가우스 조르단 소거법 <-> 가우스 소거법
기약 가우스 행렬 (Reduced Gauss matrix) [ 기약 행 사다리꼴 ]
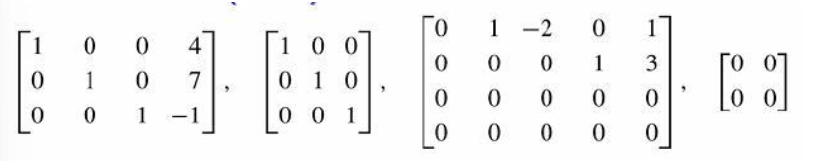
-
행의 원소가 전부 0이 아니고, 0이 아닌 첫번째 수는 1이다.
(1,2,3 번째 그림 참고, 4번의 모두 0인 것도 기약 행 사다리꼴에 들어간다.) -
모두 0으로 이루어져 있다면 모두 행렬 아래 놓인다.
(3,4번째 그림 참고) -
두 개의 연속된 행이 모두 0이 아니면 아래 행에 있는 선행1이 윗 행에 있는 선행의 오른쪽에 위치한다.
(1,2,3번째 그림 참고, 아래행의 선행이 윗행의 선행보다 오른쪽에 위치함을 알 수 있다.) -
선행 1을 가진 열은 다른 곳이 모두 0이다.
(그림 1,2,3번째 참고, 무조건 선행의 위열과 아래 열은 0.)
가우스 행렬 (Gauss matrix)
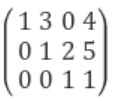
1,2,3만의 성질을 만족하는 행렬이다.
소거법-기본 행 연산
기본 행 연산법 (Elementary row operations)
(1) 한 행에 영이 아닌 상수배 (0이 아님)
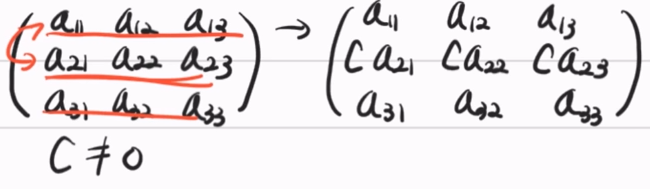
(2) 행 교환
(3) 한 행의 상수배 (0이 아님)를 다른 행에 더하기
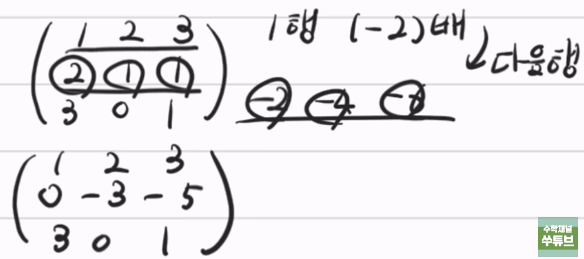
가우스 소거법 (Gaussian elimination)
- 정의: 확장 행렬을 가우스 행렬 형태로 만들어 방정식의 해를 구하는 방법
주어진 행렬이 다음과 같을 때,


-> 위에서 볼 수 있듯이 행사다리꼴 형태로 만드는 과정까지가 가우스 소거법, 한 행에서 leading 1을 제외한 나머지 원소들도 모두 0으로 만들어 기약 행사다리꼴 형태로 만드는 과정까지가 가우스 조던 소거법이다.
가우스 조던 소거법 (Gauss Jordan elimination)
확장 행렬 -> 기약 행 사다리꼴
- 확장행렬에 기본 행 연산만을 적용해 기약 가우스 행렬 형태로 만들어 방정식의 해를 구하는 방법
조르단은 가우스 소거법에 한단계를 추가하여 기약 행 사다리꼴을 만들었다.
가장 아래의 행에서 위의 행으로 연산하여 거꾸로 올라가므로 "Back Subsititution"이라고 한다.

(1) 위 행렬의 3번째 행에 -1/5를 곱하여 2번째 행에 더함으로써 두번째 행의 세번째 원소를 0으로 만든다.
(2) 위 행렬의 3번째 행에 -1을 곱하여 1번째 행에 더함으로써 첫번째 행의 세번째 원소를 0으로 만든다.
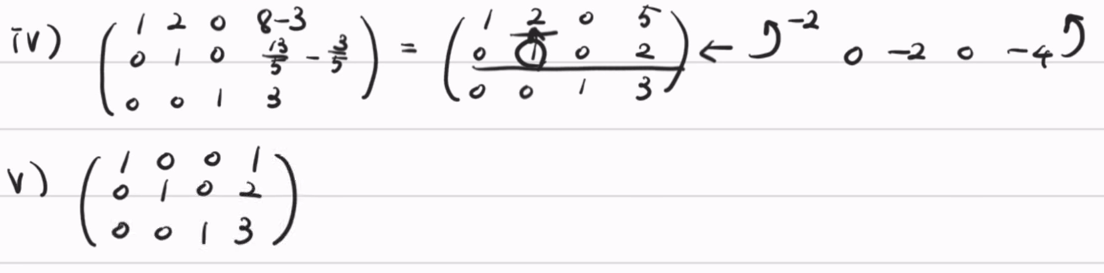
(3) 두번째 행의 leading 1 위의 원소인 2를 0으로 만들어주기 위하여 두번째 행에 -2를 곱한 값을 첫번째 행에 더한다.
결국 위 행렬에서 x = 1, y = 2, z = 3으로 해를 구할 수 있게 된다.
위의 계산 과정에서는 행교환이 쓰이지 않았다.
행교환이 쓰이는 경우는 아래와 같이 특수한 경우이다.
(1) 첫 행의 첫번째 원소가 0이므로 1행을 2행 또는 3행과 교환해야 한다.
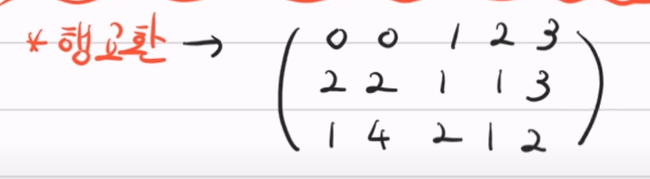
아래와 같이 1행, 2행, 3행의 첫번째 원소가 모두 0인 경우는 x에 관해 무수히 많은 해가 존재한다는 것이므로 생각할 필요가 없다.
