백준 7562 BFS 풀이

문제

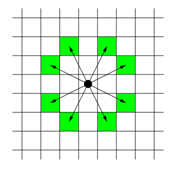
체스판 위에 한 나이트가 놓여져 있다. 나이트가 한 번에 이동할 수 있는 칸은 아래 그림에 나와있다. 나이트가 이동하려고 하는 칸이 주어진다. 나이트는 몇 번 움직이면 이 칸으로 이동할 수 있을까?

입력

입력의 첫째 줄에는 테스트 케이스의 개수가 주어진다.

각 테스트 케이스는 세 줄로 이루어져 있다. 첫째 줄에는 체스판의 한 변의 길이 l(4 ≤ l ≤ 300)이 주어진다. 체스판의 크기는 l × l이다. 체스판의 각 칸은 두 수의 쌍 {0, ..., l-1} × {0, ..., l-1}로 나타낼 수 있다. 둘째 줄과 셋째 줄에는 나이트가 현재 있는 칸, 나이트가 이동하려고 하는 칸이 주어진다.

출력

각 테스트 케이스마다 나이트가 최소 몇 번만에 이동할 수 있는지 출력한다.

풀이 방법

시작 위치에서, 목적지 위치까지 최소의 이동횟수로 가는 방법을 찾는 문제이다. 이러한 문제는 DFS보다 BFS가 더 효율적으로 작동 할 것이다. BFS 넓이 우선 탐색을 나이트의 8방향으로 진행하다가 해당 원소에 도착하면 바로 해당 인덱스의 값을 return해주면 된다. 하지만, 이 문제는 TEST 케이스가 여러개 일 수 있으므로 방문한 횟수와 방문을 했다는 표시를 다시 reset해주는 memset()을 사용해줘야 한다.

코드

#include<iostream>
#include<queue>
#include<algorithm>
#include<string.h>


using namespace std;

#define MAX 300

int l;
int iter;

int arr[MAX][MAX];
bool visited[MAX][MAX];


struct Dir
{
    int x; 
    int y;
    
    Dir(int nx, int ny) : x(nx), y(ny) { }
    Dir() { }
};

Dir startDir;
Dir goalDir;

Dir nightDir[8] = {{1,2},{1,-2},{2,1},{2,-1},{-1,2},{-1,-2},{-2,1},{-2,-1}};


int bfs()
{
    queue<Dir> q;
    q.push(startDir);
    visited[startDir.x][startDir.y] = true;

    while(!q.empty())
    {
        int x = q.front().x;
        int y = q.front().y;
        q.pop();

        if(x == goalDir.x && y == goalDir.y)
            return arr[x][y];

        for(int i = 0; i < 8; ++i)
        {
            int nx = x + nightDir[i].x;
            int ny = y + nightDir[i].y;

            if(nx < 0 || ny < 0 || nx >= l || ny >= l)
                continue;
            
            if(visited[nx][ny] == false)
            {
                arr[nx][ny] = arr[x][y] + 1;
                visited[nx][ny] = true;
                q.push(Dir(nx,ny));
            }
        }
    }

    return -1;
}

void init()
{
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
}

int main()
{
    init();
    cin >> iter;

    for(int i = 0; i < iter; ++i)
    {
        cin >> l;
        
        cin >> startDir.x >> startDir.y;
        cin >> goalDir.x >> goalDir.y;

        cout << bfs() << '\n';
        memset(visited,false,sizeof(visited));
        memset(arr,0,sizeof(arr));
    }


    return 0;
}