
1. 선형 검색
- 선형검색: 선형으로 나열되어 있는 데이터를 순차적으로 스캔하면서 원하는 값을 찾는다.

- 보초법: 마지막 인덱스에 찾으려는 값을 추가해서 찾는 과정을 간략화한다 .

2. 이진 검색
- 이진 검색: 정렬되어 있는 자료구조에서 중앙값과의 크고 작음을 이용해서 데이터를 검색한다.
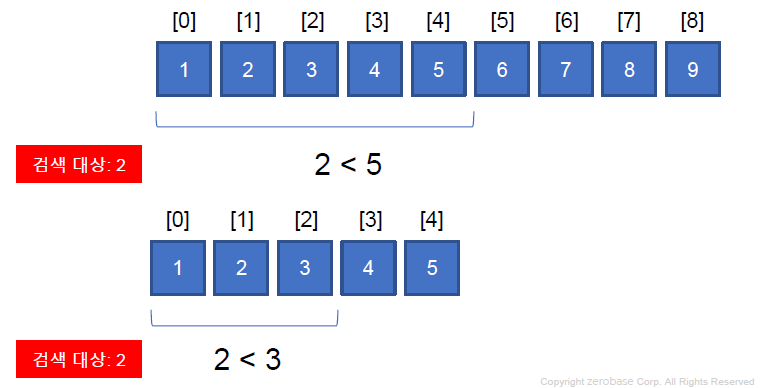
정렬이 되어있어야 한다.
3. 순위
- 순위: 수의 크고 작음을 이용해서 수의 순서를 정하는 것을 순위라고 한다.
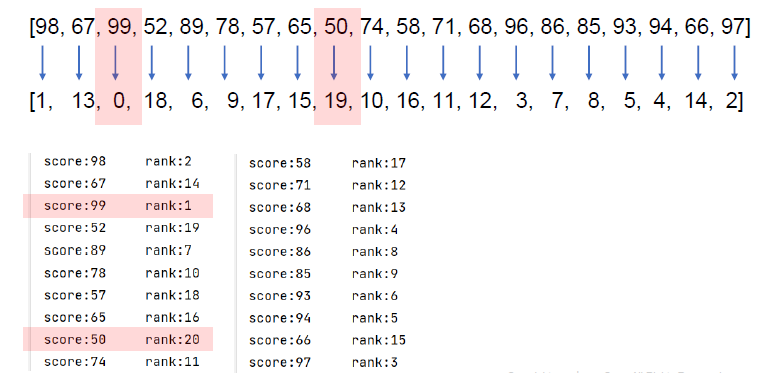
4. 버블 정렬
- 버블 정렬: 처음부터 끝까지 인접하는 인덱스의 값을 순차적으로 비교하면서 큰 숫자를 가장 끝으로 옮기는 알고리즘이다.
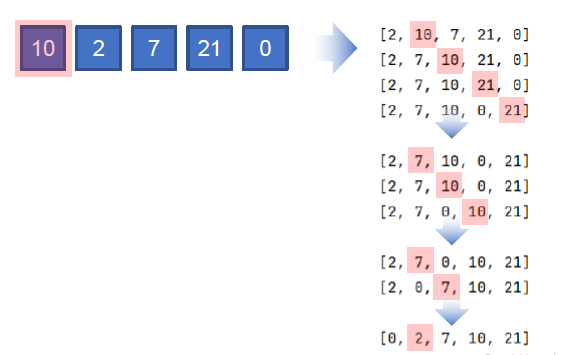
5. 삽입 정렬
- 삽입 정렬: 정렬되어 있는 자료 배열과 비교해서, 정렬 위치를 찾는다.
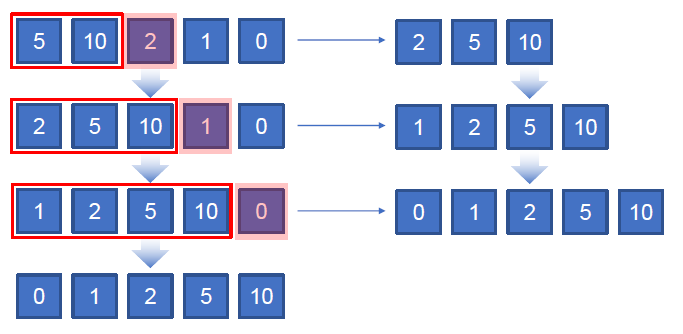
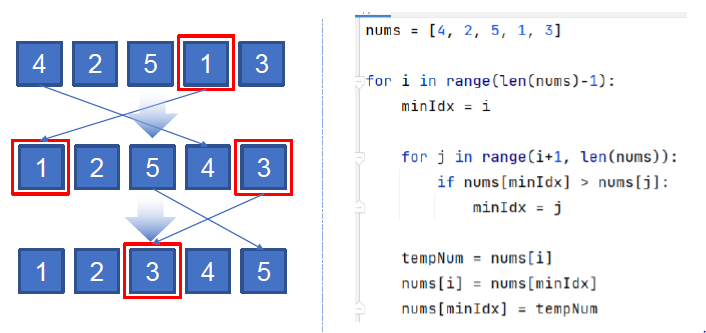
6. 선택 정렬
- 선택 정렬: 주어진 리스트 중에 최소값을 찾아, 그 값을 맨 앞에 위치한 값과 교체하는 방식으로 자료를 정렬하는 알고리즘이다.
7. 최댓값
- 자료구조에서 가장 큰 값을 찾는다.
class MaxAlgorithm:
def __init__(self, ns):
self.nums = ns
self.maxNum = 0
def getMaxNum(self):
self.maxNum = self.nums[0]
for n in self.nums:
if self.maxNum < n:
self.maxNum = n
return self.maxNum
ma = MaxAlgorithm([-2, -4, 5, 7, 10])
maxNum = ma.getMaxNum()
print(f'maxNum: {maxNum}')8. 최솟값
- 자료구조에서 가장 작은 값을 찾는다.
class MinAlgorithm:
def __init__(self, ns):
self.nums = ns
self.minNum = 0
def getMinNum(self):
self.minNum = self.nums[0]
for n in self.nums:
if self.minNum > n:
self.minNum = n
return self.minNum
ma = MinAlgorithm([-2, -4, 5, 7, 10])
minNum = ma.getMinNum()
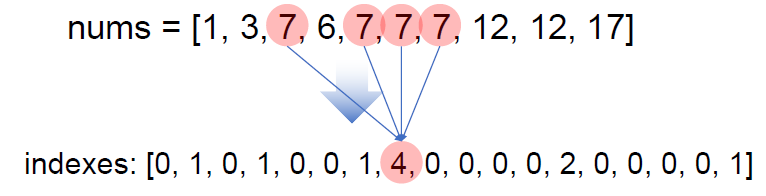
print(f'minNum: {minNum}')9. 최빈값
- 데이터에서 빈도수가 가장 많은 데이터를 최빈값이라고 한다.
class MaxAlgorithm:
def __init__(self, ns):
self.nums = ns
self.maxNum = 0
self.maxNumIdx = 0
def setMatIdxAndNum(self):
self.maxNum = self.nums[0]
self.maxNumIdx = 0
for i, n in enumerate(self.nums):
if self.maxNum < n:
self.maxNum = n
self.maxNumIdx = i
def getMaxNum(self):
return self.maxNum
def getMaxNumIdx(self):
return self.maxNumIdx
nums = [1,3,7,0,7,7,7,12,12,17]
maxAlo = MaxAlgorithm(nums)
maxAlo.setMatIdxAndNum()
maxNum = maxAlo.getMaxNum()
print(f'maxNum: {maxNum}')
indexes = [0 for i in range(maxNum+1)]
print(f'indexes: {indexes}')
print(f'indexes length: {len(indexes)}')
for n in nums:
indexes[n] = indexes[n] + 1
print(f'indexed: {indexes}')
maxAlo = MaxAlgorithm(indexes)
maxAlo.setMatIdxAndNum()
maxNum = maxAlo.getMaxNum()
maxNumIdx = maxAlo.getMaxNumIdx()
print(f'maxNum: {maxNum}')
print(f'maxNumIdx: {maxNumIdx}')
print(f'즉, {maxNumIdx}의 빈도수가 {maxNum}로 가장 높다')10. 근삿값
- 특정 값(참값)에 가장 가까운 값을 근삿값이라고 한다.
import random
nums = random.sample(range(0, 50), 20)
print(f'nums: {nums}')
inputNum = int(input('input number: '))
print(f'inputNum: {inputNum}')
nearNum = 0
minNum = 50
for n in nums:
absNum = abs(n - inputNum)
if absNum < minNum:
minNum = absNum
nearNum = n
print(f'nearNum: {nearNum}')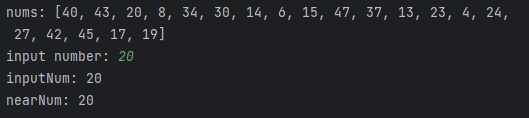
11. 평균
- 수나 양의 중간값을 갖는 수를 평균이라고 한다.
import random
nums = random.sample(range(0,100), 10)
print(f'nums: {nums}')
total = 0
for n in nums:
total += n
average = total / len(nums)
print(f'average: {average}')
#50이상 90이하 수들의 평균
import random
nums = random.sample(range(0,100), 10)
print(f'nums: {nums}')
total = 0
targetNums = []
for n in nums:
if n >= 50 and n <= 90:
total += n
targetNums.append(n)
average = total / len(targetNums)
print(f'targetNums: {targetNums}')
print(f'average: {average}')12. 재귀
- 나 자신을 다시 호출하는 것을 재귀라고 한다 .

def recusion(num):
if num > 0:
print('*'*num)
return recusion(num-1)
return 1
recusion(10)
13. 하노이의 탑
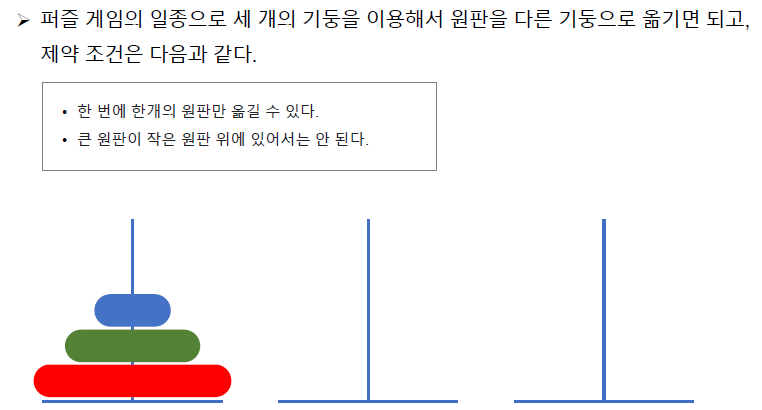
#원판 개수, 출발 기둥, 도착 기둥, 경유 기둥
def moveDisc(discCnt, fromBar, toBar, viaBar):
if discCnt == 1:
print(f'{discCnt}disc를 {fromBar}에서 {toBar}로 이동')
else:
#(discCnt-1)개들을 경유 기둥으로 이동
moveDisc(discCnt-1, fromBar, viaBar, toBar)
#discCnt를 목적 기둥으로 이동
print(f'{discCnt}disc를 {fromBar}에서 {toBar}로 이동')
#(discCnt-1)개들을 도착 기둥으로 이동
moveDisc(discCnt-1, viaBar, toBar, fromBar)
moveDisc(3,1,3,2)14. 병합 정렬
- 자료구조를 분할하고 각각의 분할된 자료구조를 정렬한 후 다시 병합하여 정렬한다.
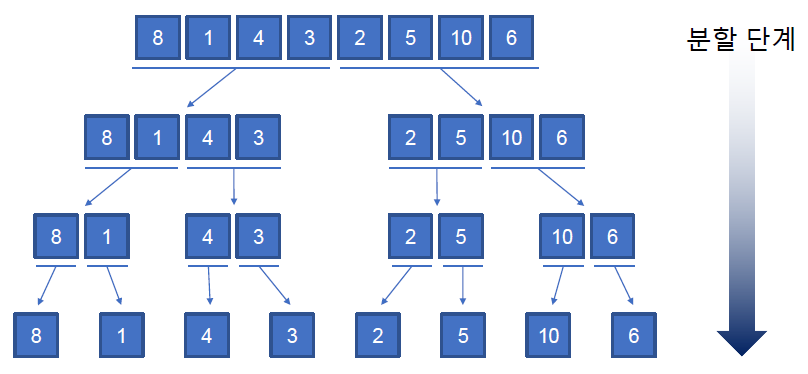
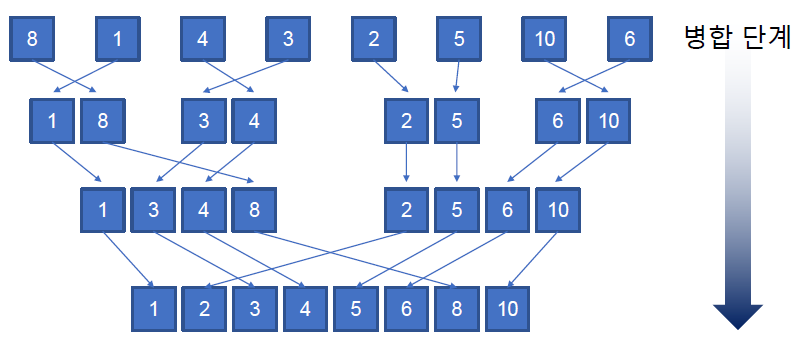
def mSort(ns):
if len(ns) < 2:
return ns
midIdx = len(ns) // 2
leftNums = mSort(ns[0:midIdx])
rightNums = mSort(ns[midIdx:len(ns)])
mergeNums = []
leftIdx = 0; rightIdx = 0
while leftIdx < len(leftNums) and rightIdx < len(rightNums):
if leftNums[leftIdx] < rightNums[rightIdx]:
mergeNums.append(leftNums[leftIdx])
leftIdx += 1
else:
mergeNums.append(rightNums[rightIdx])
rightIdx += 1
mergeNums = mergeNums + leftNums[leftIdx:]
mergeNums = mergeNums + rightNums[rightIdx:]
return mergeNums
nums = [8,1,4,3,2,5,10,6]
print(f'mSort(nums): {mSort(nums)}')
- 퀵 정렬
- 값보다 작은 값과 큰 값으로 분리한 후 다시 합친다.
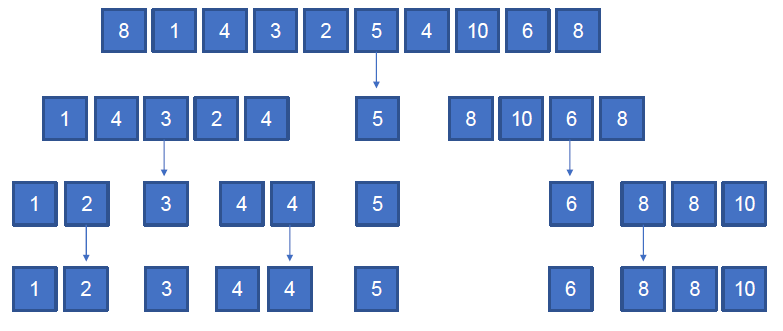
def qSort(ns):
if len(ns) < 2:
return ns
midIdx = len(ns) // 2
midVal = ns[midIdx]
smallNums = []; sameNums = []; bigNums = []
for n in ns:
if n < midVal:
smallNums.append(n)
elif n == midVal:
sameNums.append(n)
else:
bigNums.append(n)
return qSort(smallNums) + sameNums + qSort(bigNums)
nums = [8,1,4,3,2,5,4,10,6,8]
print(f'qSort(nums): {qSort(nums)}')