ML 1-4 선형 회귀

1. 선형 회귀 Linear Regression

선형적으로, 그래프에서 직선 1개만 그려서 예측하는 방법.
간단하지만 강력하다.

(머신러닝 초기) '세상의 모든 법칙은 선형적'이라는 가정으로 문제에 접근했다.

ex 커피를 많이 마실수록 시험을 잘 본다.
-> 선형이라고 가정할 때 가능했던 문제가 많았다.

현재는 선형으로 풀 수 없는 문제, 선형이 아닐 때 풀 수 있는 문제들도 많아졌다.

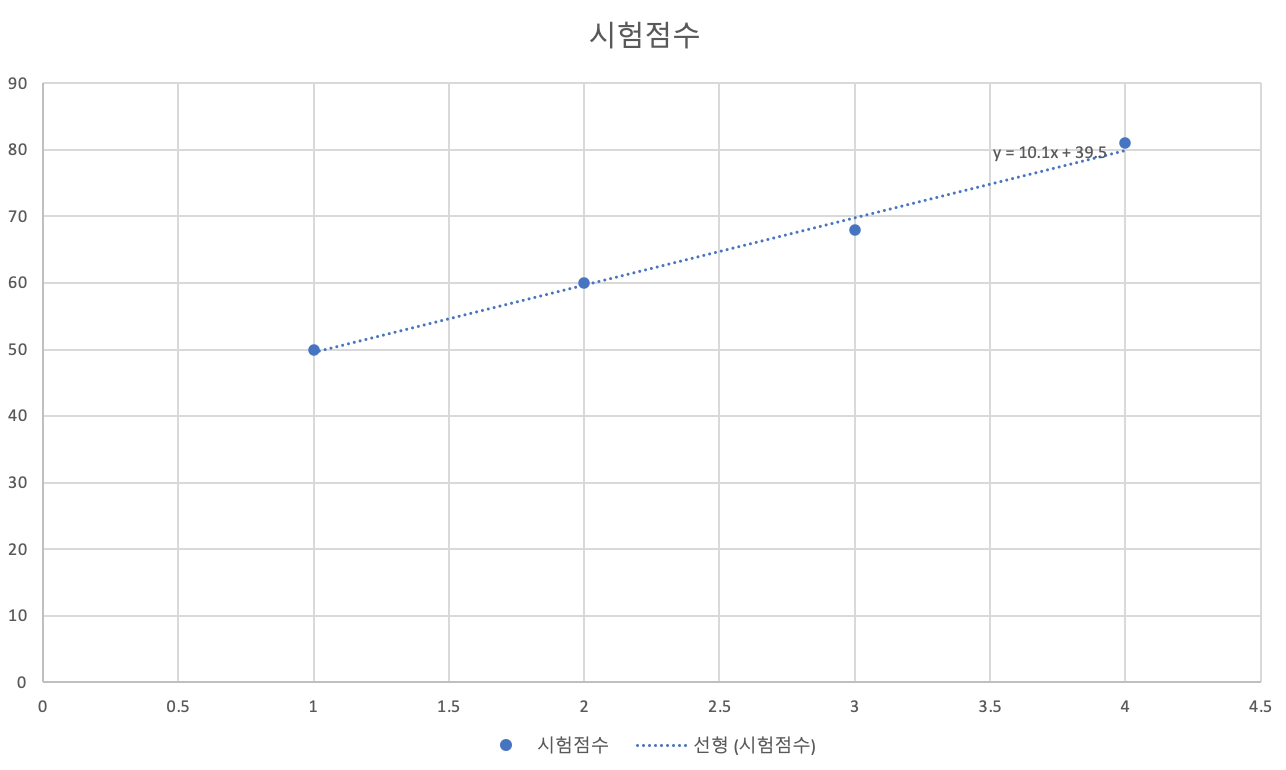
아래와 같이 임의의 직선 1개로 표현할 수 있다.

가설 Hypothesis

$H(x) = Wx + b$

# 일차 함수
W (Weight) : 기울기
b (bias) : y절편

# 행렬matrix 형태

머신러닝의 모든 문제는 가설이 있어야 풀 수 있다.
사람이 가설을 정하고 기계가 가설에 맞춰 문제를 풀도록 학습시킨다.
선형 회귀는 어떤 문제를 풀 때 선형이 효과적이라 판단하고 선형이라는 가설을 세운 것.

데이터셋 (실험한 결과)

커피 수	시험 점수 (정답값)
1	50
2	60
3	68
4	81

점과 선이 가까워지도록 학습시켜야 한다.
기울기가 다르면 점-선간 거리가 멀어지고 예측이 잘못된다.

Cost Function 손실함수

점-선간 간격이 작아지도록 학습시키기 위해 쓰는 개념.
내가 가설(직선)을 세웠을 때, 정답값(점)과의 거리를 계산한 것.

$Cost = {{1\over N}\sum_{i=1}^{N}{(H(x_i) - y_i) ^ 2}}$

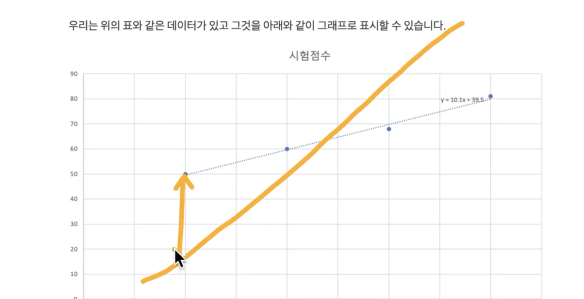
점-선 사이의 거리가 멀수록 값이 커진다.
학습이 잘 되는지, 어느 방향으로 시켜야 하는지를 파악할 수 있다.
Cost Function(=Loss Function)이 작게 나오면 잘 학습된 것.

• Mean Squared Error 평균 제곱 오차
  직선-정답의 거리

• 최적화 minimization, optimization
  Cost가 minimize되는 방향으로 학습을 시킨다.

머신러닝 엔지니어의 역할

가설을 세우고 손실함수를 정의한다.
어떤 가설과 손실함수가 좋은지는 여러번의 반복 실험을 통해서 찾아간다.

머신러닝

사람이 정한 가설과 손실함수로 계산해서 Cost가 최소가 되는 값을 찾는다.

우리는 가설을 통해 W와 b의 값을 알아내야 한다.
가설값과 정답값의 차이를 비교해 보고, W-b를 바꿔 가며 Cost Function이 낮아지는 값을 찾는 것.
-> 을 기계한테 시킨다.