lower bound는 한국말로 '하한' 이라는 의미다.
5의 lower bound는, 5 이상의 값이 나오는 최초의 위치이다.
반면 upper bound는 한국말로 '상한' 이라는 의미이다.
5의 upper bound는, 5 초과의 값이 나오는 최초의 위치이다.
이 때, 이분탐색에서 lower bound, upper bound 를 구할 때 주의점이 한가지 있다.
바로, 데이터들의 최대값보다 큰 값, 혹은 최소값보다 작은 값을 구할 경우에 문제가 된다.
1. Lower Bound
(1) 데이터의 최대값보다 큰 값의 lower bound
<문제 조건>
[0, 1, 3, 5, 5, 5, 7, 9, 9, 10, 10, 12, 14] 배열에서 15의 lower bound를 찾아라
먼저 다음처럼 lower bound를 구하고자 하는 이진 탐색 함수를 작성했다고 하자.
public static int getLowerBound(int[] arr, int h){
int l = 0, r = arr.length-1;
while(l < r) {
int mid = (l + r) / 2;
if (arr[mid] < h) {
l = mid + 1;
} else {
r = mid;
}
}
return l;
}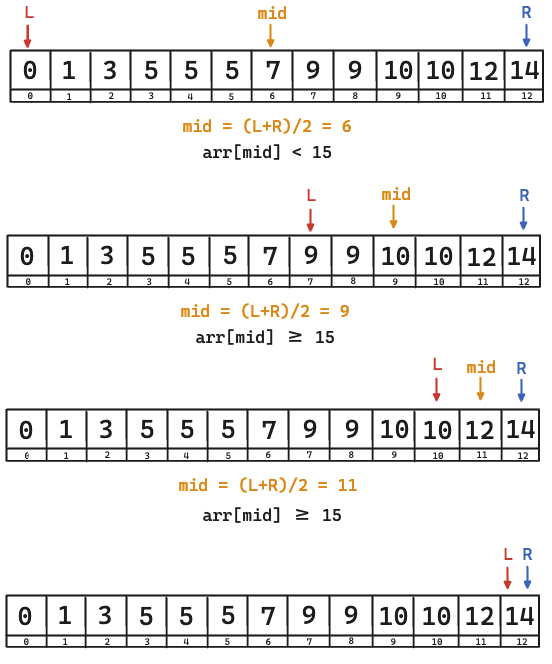
그럼 답은 12가 나온다.
내가 원한 값은 13이어야 할텐데, 12가 나온다는 것은 문제가 된다.
문제의 원인은, 오른쪽 끝 원소의 위치가 항상 탐색 값보다 작다는 것이 가장 큰 문제이다.
이는 두가지로 해결할 수 있다.
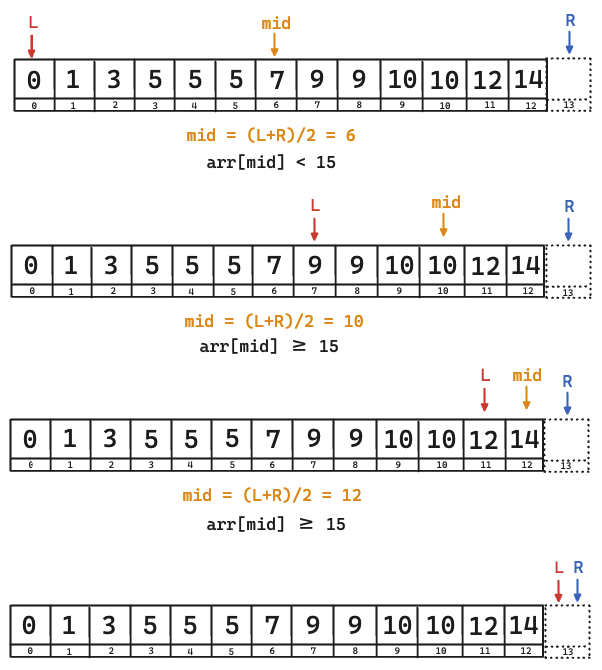
(1) 오른쪽 끝을 arr의 배열의 크기로 두자 (마지막 index + 1)
오른쪽 끝 원소의 위치가 항상 탐색 값보다 작다는 것을 해결하기 위해, 임시의 index를 추가한 것이다.
이렇게 추가해도 문제가 없는 이유는, 해당 배열 범위의 최대값보다 작은 데이터를 탐색한다면, 어차피 R 은 유효한 index내로 이동할 것이다.
만일 그렇지 않은 경우에, 하한선은 R의 위치가 되어 문제의 조건을 만족한다.
public static int getLowerBound(int[] arr, int h){
int l = 0, r = arr.length;
while(l < r) {
int mid = (l + r) / 2;
if (arr[mid] < h) {
l = mid + 1;
} else {
r = mid;
}
}
return l;
}
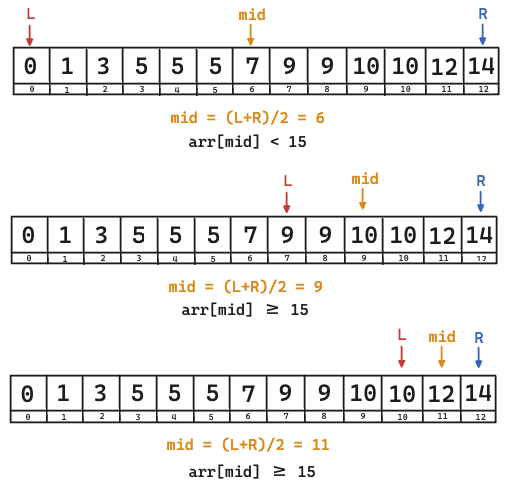
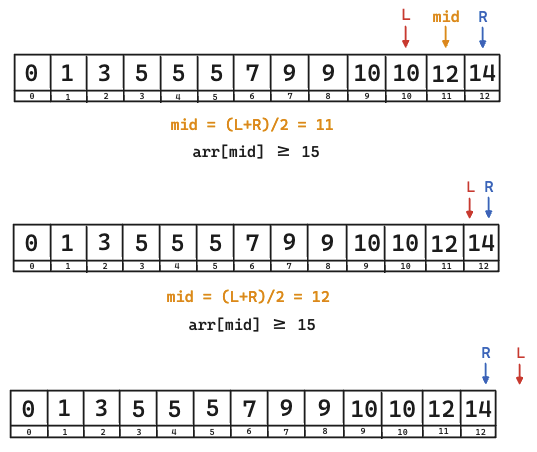
(2) 구현문을 바꿔버리자
구현된 코드의 문제점은 l==r 의 위치인 12에서 반복문이 끝나기 때문이다.
이를 해결하기 위해서는, 해당 반복문을 빠져나갈 수 있게 while 반복문에 등호를 포함시키고,
이를 종료할 수 있게하는 l과 r의 조건을 상정하면 된다.
당연히 l = mid + 1 로 유지이고, r = mid - 1 로 변경해서, r의 종료도 신경쓰자.
public static int getLowerBound(int[] arr, int h){
int l = 0, r = arr.length;
while(l <= r) {
int mid = (l + r) / 2;
if (arr[mid] < h) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return l;
}
(2) 데이터의 최소값보다 작은 값의 lower bound
이 경우는 lower bound가 존재할 수가 없다.
2. Upper Bound
Lower Bound와 원리는 마찬가지다. 다음 두가지 코드로 구현 가능하다.
public static int upper(int x, int[] arr){
int l = 0, r = arr.length;
while(l < r){
int mid = (l+r)/2;
if(arr[mid] > x){
r = mid;
}
else{
l = mid+1;
}
}
return l;
}public static int upper(int x, int[] arr){
int l = 0, r = arr.length-1;
while(l <= r){
int mid = (l+r)/2;
if(arr[mid] > x){
r = mid-1;
}
else{
l = mid+1;
}
}
return l;
}마무리
개인적으로 while(l<r) 코드를 많이 작성해서, 하나만 외워서 사용하면 좋을 것 같다.
