Paging
- 프로그램을 구성하는 논리적인 메모리를 동일한 크기의 page로 자른 후 각각의 page별로 물리적인 메모리의 적당한 위치에 올리는 기법
- 물리적인 메모리에 프로그램을 통째로 올리는 연속 할당 방식은 각각의 프로그램을 물리적인 메모리에 올려 놓을 때 주소 변환이 간단했음
- paging은 단지 각 프로그램의 시작위치 만으로는 주소 변환을 할 수 없음, 페이지 별 주소 변환이 필요
- 주소 변환을 위한 page table이 필요함
- 짜투리 공간 때문에 내부조각 발생할 수 있음
- 페이지크기 그대로 들어가기 때문에 외부조각 발생 X

page table(배열의 practical한 표현)
-
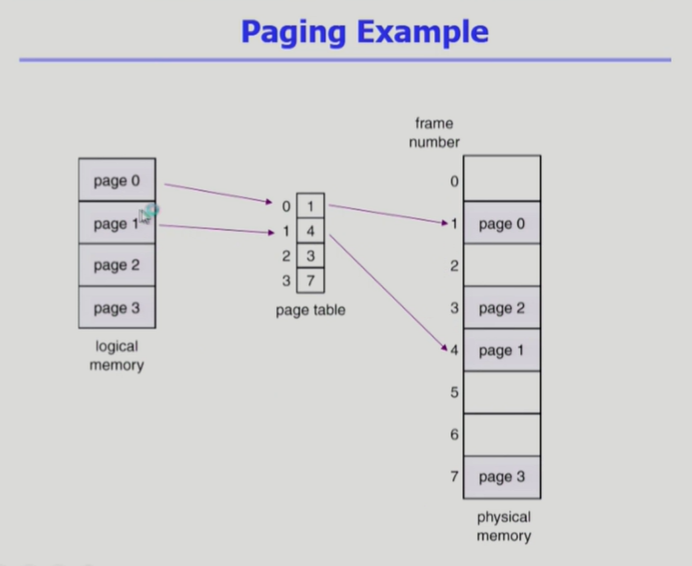
paging 기법에서 논리주소를 물리주소로 변환하기 위해 각 페이지마다 매핑되는 물리주소의 값을 저장해놓은 배열
-
페이지 개수 만큼 페이지 entry 존재, 각각의 entry에는 몇 번 물리적인 페이지에 올라갔는지 나타내고 있음
-
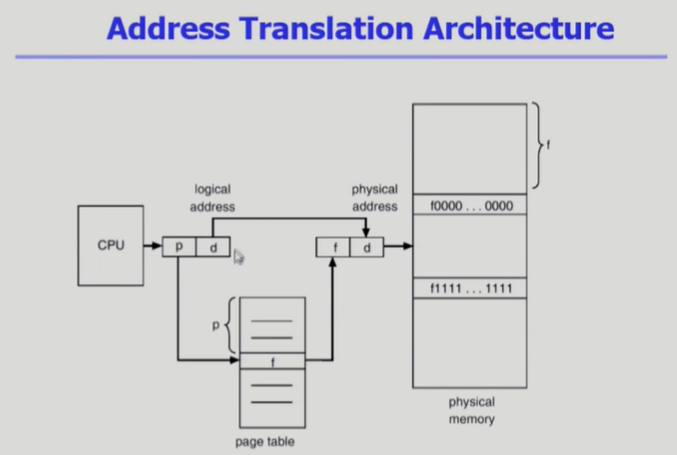
p는 페이지 번호, d는 해당 페이지에서 얼만큼 떨어져있는지 나타내는 offset
-
f는 physical memory에서 얼마나 떨어져 있는 frame인지, d는 해당 frame으로부터 떨어져야 할 offset
Q.paging 기법에서 cpu가 확인하는 프로세스의 logical address의 예시를 보여줄 수 있어? logical address에서 page 번호와 entry에서 떨어져있는 위치인 offset을 어떻게 표시해?


Q.프로세스 롣, 실행, 테이블 작성 등의 순서는 어떻게 되지?

Implementation of Page Table
-
페이지 테이블이 어디에 들어가야 할까?
- 페이지 테이블은 main memory에 상주하면서 각 페이지가 CPU에서 수행될 때 물리주소를 매핑하기 위해 사용함
- 프로그램을 구성하는 주소 공간을 page 단위로 자르는데 이 page 크기가 보통 4kb, 4kb로 자르면 entry가 실제로 100만개가 필요(32비트 주소체계 가상 메모리 최대 크기인 4GB를 분할)
- 그러면 100만개 entry가 cpu의 register에 들어갈 수 있음? 없다. 용량이 크다. 프로그램마다 page table이 여러개 존재하기 때문에 더더욱 넣을 수 없다. 캐시에 들어가기에도 용량이 크다. 그래서 결국.. page table은 메모리에 넣는다.
-
page table의 구성과 접근

- MMU에서의 base register와 limit register가 PTBR과 PTLR로 바뀜
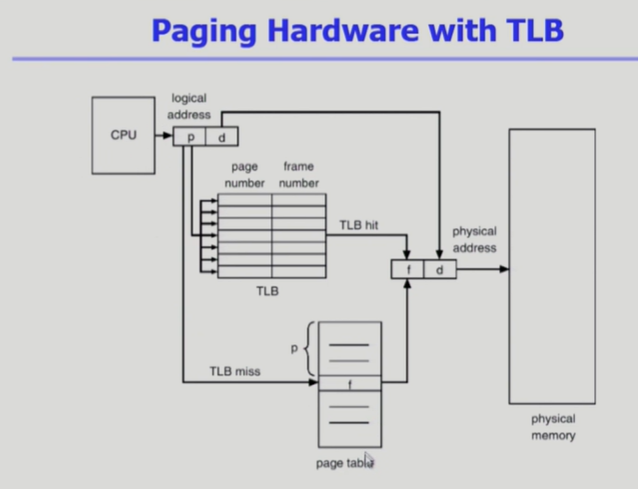
- 2번의 메모리 접근은 속도가 느리기 때문에 메인 메모리보다 빠르게 주소 변환을 해주는 TLB라는 HW(일종의 캐시메모리)를 사용
- 메모리 상 page table에 접근하기 전에 TLB에 먼저 접근하여 확인
- TLB miss에 경우 page table을 통해서 2번의 메모리 접근을 하는 방식을 사용
- 논리적인 page번호 p와 p에 대한 주소변환된 프레임 번호 f를 쌍으로 가지고 있음, page table은 p를 알면 page table에서 p만큼 떨어진 곳에 저장된 f를 알 수 있지만 TLB는 전체 정보를 가지고 있지 않기 때문에 page number가 p로 저장되어 있어야 하고, 여기에 해당하는 frame number도 같이 저장해야 함(page table은 모든 page를 가지지만, TLB는 자주 접근한 일부 page 정보만을 가지고 있기에 인덱스 접근이 불가함)
- page table에서는 배열의 index가 p인 곳에 접근하면 됐지만, TLB는 값이 p인 걸 직접 찾아야 한다.
- TLB는 전체를 search 해야 하는데 이것이 오래 걸리기 때문에 assosiactive register을 이용하여 parralel search를 이용
- TLB는 process마다 주소변환 정보가 다르기 때문에 context switch때 마다 flush 함

- TLB miss면 최악의 상황이니까 더 오래걸릴텐데 TLB search가 아주 적게 걸리지 않는 이상 miss가 나지 않도록 TLB 구성이 잘 이루어져야 할 거 같은데?

- 실제로 메모리 접근하는 시간? lookup time인 입실론은 1보다 매우 작은 수이며, Hit ratio 알파는 굉장히 높음(1에 가까움), 따라서 page table만 있을 때보다 훨씬 빠름
Two-level Page Table

-
실제 시스템에서는 page를 2개 사용한다. Two-level Page Table
-
2개의 page table 이용하여 outer table에서 1번 변환 후 그 다음 table에서 한 번 더 변환하여 물리주소를 얻음
-
사용하는 이유: page table을 2번 접근해야 해서 속도를 줄어들지 않지만 page table이 차지하는 공간의 크기가 작아짐
-
현대 컴퓨터에서는 메모리 주소체계가 32bit, 62bit를 사용
-
32bit 기준으로 설명하면 2^32 만큼의 정보를 표현할 수 있음
- 2^32는 약 4G, 2^10 = K(천) , 2^20 = M(100만), 2^30 = G(10억)
- 2^32B는 4GB 표현 가능
-
4GB 공간을 page 단위인 4KB로 쪼개면 page 100만 개가 나옴, 100만개의 entry가 필요
-
각 프로세스마다 100만개의 entry가 있는 page table을 모두 메모리에 올리면 공간 낭비가 심함(각 프로그램마다 4B * 100만 필요)
-
실제 프로그램은 4GB 중 일부분의 공간만 사용하는 경우가 많으나 page table은 index를 통해 접근하기 때문에 사용하지 않는 공간이 있다고 해서 거기에 해당하는 logical address를 비우고 압축해서 table을 만들 수 없음, 일부 공간만 사용한다 해도 page table은 전체 4gb에 해당하는 entry를 가지고 만들어야함. 이를 해결하기 위해 2단계 테이블 사용
-
2단계 table에서 공간을 절약할 수 있는 이유
-
어떻게 공간을 절약할 수 있을까?
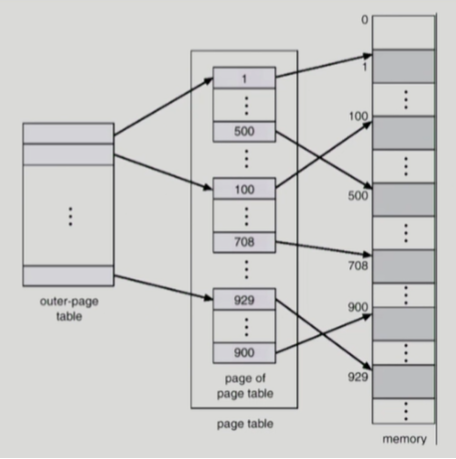
- 실생활 주소체계에서 서울시 관악구 봉천동처럼 entry를 쪼개서 바로 접근하도록 한다. 이때 관악구에는 비어있는 공간이 있을 수 있다. 이 비어있는 공간에 대해서는 page table 내에서 공간을 생성하지 않으면 공간을 절약할 수 있다. page table이 1개일 때는 page table에 접근할 때 각 index로 접근하면서 물리주소를 매핑해주었는데, 이때 메모리 시작위치에서 얼마나 떨어져있는지에 따라 메모리 주소가 매핑되면서 비어있는 공간들에 대해서도 배열이 만들어질 수밖에 없어서 공간이 낭비됐다.
- outer page에 각 페이지에 대한 entry를 저장하고, inner page에는 해당 페이지 내에서 byte 단위의 entry를 저장한다. 이때 사용하지 않는 page에 대해서는 outer page에서 pointer로 null로 만들어 inner page에서 entry를 생성하지 않아 공간을 절약할 수 있다.
- 뭔가 이상한데 그럼 page table이 1개일 때도 사용하지 않는 공간에 대해서 null 처리를 하면 되는 거 아님..?
- page가 1개일 때는 page table의 시작 위치로부터 몇 번째 entry인지 index를 가지고 접근하기 때문에 중간에 사용하지 않는 page 영역이 있다고 해서 배열을 자르고 page를 만들 수가 없다. 하지만 outer를 쓰면 각각의 page의 시작위치에 대해서 우선 pointer를 만드는데, 이 때 각 페이지 중 사용하지 않는 page에 대해서 null pointer 처리를 하면 inner page에서는 중간에 사용되지 않는 영역을 자를 수 있게 되는 것이다.
- 아래 그림에서 보면 outer page는 프로그램 전체 4GB에 대한 각 페이지(4KB)의 시작위치를 모두 저장한다. 하지만 이 시작 위치가 가리키는 innter page 값을 null pointer 처리하면 inner page에서는 그 페이지에 대한 배열이 생성되지 않기 때문에 공간이 절약된다.
Two-Level Paging Example

- logical adderss에서 p1, p2, d는 각각 몇 bit로 표현되어야 할까
- page 하나의 크기가 4KB이기 때문에 4KB안에서 BYTE 단위로 주소 구분을 하려면 몇 비트가 필요할까, 2^12의 위치를 구분해야 함(2^10=K * 2^2 = 4), 따라서 offset인 d를 위해서 12비트가 필요
- 안쪽 테이블은 각 페이지별 entry가 4Byte로 이루어지므로 4KB / 4B인 1K개의 위치를 구분하기 위해, 10비트가 필요
- 바깥 페이지는 남은 10비트로 표현 -> inner page는 4GB / 4KB 로 1M개, 1M개를 페이지 별 entry 개수 1K로 내누면 outer page는 1K개 이므로 표현 가능
Q.만약 64bit 체계라면?
-
모르겠는 부분
-
1.page 크기는 어떻게 결정하는가
-
2.entry 크기는 어떻게 결정하는가
-
3.만약 page 크기가 정해져서 각 page당 시작위치(기준주소)의 개수가 정해지면 그걸 가지고 outer page를 구성하는게 맞는가? 아니면 p2, d를 제외한 나머지 bit로 outer page에서 각 page를 더욱 쪼갤 수 있는 것인가?
-
모르겠다... 아래 글 참고
https://jyeonnyang2.tistory.com/78
-
안쪽 페이지 테이블은 메모리 상 페이지 크기와 같음, 페이지 하나의 크기가 4KB이므로 안쪽 페이지 테이블의 크기도 4KB, 각 페이지 당 1K개의 entry가 존재
-
2단계 페이지 테이블 방법은 1단계에서 쓰던 page table + outer page까지 필요해서 사실은 공간적으로 더 손해일 수 있음, 하지만 프로그램의 logical address는 꽉 채워져 있는 것이 아니라 중간 부분이 상당히 비워져 있다고 했음, 2단계 방식을 사용하면 안쪽 테이블에서 이 비어있는 부분은 null pointer로 남겨두어 메모리를 사용하지 않기 때문에 메모리 공간을 덜 차지하게 됨.
좋은 정보 얻어갑니다, 감사합니다.