고려대학교 산업공학과 정태수 교수님 강의 정리
Week2: 동적계획법-1
2-1. 문제해결전략과 동적 계획법
수학적 귀납법
정의
을 참 또는 거짓인 명제라고 하자.
- 이 참이고,
- 모든 에 대해 이 참일 때, 도 참이라면,
- 이 참이다.
예시
- n이 1일 때 참인지 체크
- n=1:
- -> (이 사실일 때)
- 좌항:
==> - 우항:
- 좌항:
재귀식
과 의 관계: =
==> 의 정보를 알고있으면 계산 가능
==> 재귀식(recursive equation)을 통해 문제 해결
도입 예시
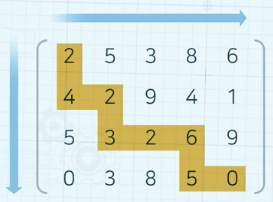
최소 비용 경로 정의
- 각 칸의 숫자는 해당 위치 별 비용
- 진행 방향은 오른쪽, 아래만 가능
- 위 그림의 경로 비용: 2+4+2+3+2+6+5+0
좌상단에서 우하단으로 최소비용으로 이동하는 방법
- 가장 단순한 방법
- 좌상단에서 우하단까지 경로 모두 나열
- 경로 별 비용 계산
- 가장 적은 비용 경로 탐색
- 스마트한 방법
- 정의: : 에서 로 가는데 소요되는 최소 비용
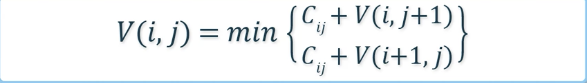
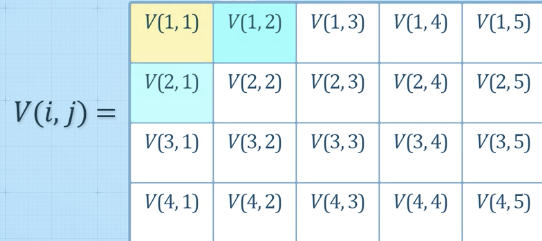
- V(i,j) 계산 방법 --> 재귀식

- 의 최소 경로 비용: 24
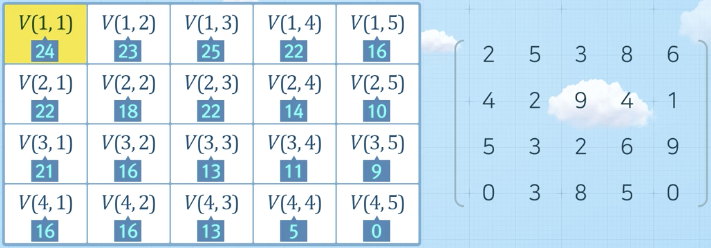
- 정의: : 에서 로 가는데 소요되는 최소 비용
어떤 경로를 가야 최소 비용인 24를 얻을 수 있을까?
- 재귀식을 바탕으로 우하단에서 좌상단으로 값 순차 계산
- 최소비용을 따라 우측이나 좌측으로 화살표
==> 최소비용 방향 파악을 위한 기록
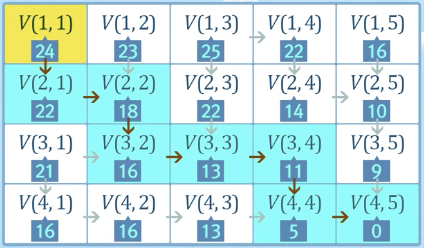
문제 해결
탐욕알고리즘 (Greedy Algorithm)
-
정의
- 탐욕알고리즘: 매 순간 최선의 선택
(매 순간 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 최적해에 도달하는 기법)
- 탐욕알고리즘: 매 순간 최선의 선택
-
동적계획법과 차이
- 동적계획법: 현재 뿐만 아니라 미래도 함께 고려
-
최소경로 탐색 예시

분할정복 알고리즘 (Divide-and-conquer algorithm)
- 문제를 작은 문제로 분할 (divide)
- 작은 문제들 각각 정복 (conquer)
- 작은 문제에 대한 해답 통합 (combine)
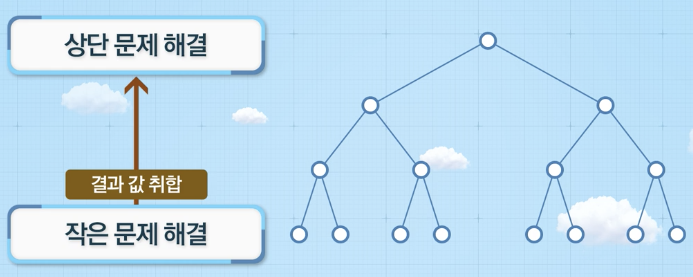
동적 계획법 (Dynamic Programming)
- Overlapping subproblems
- 중첩된 작은 문제들로 단순화
- 재귀적 구조 활용
- 부분 문제부터 순차 해결(=> 원래 문제를 해결)
- 하위 문제 해결
- 결과 값 이용
- 상위 문제 해결
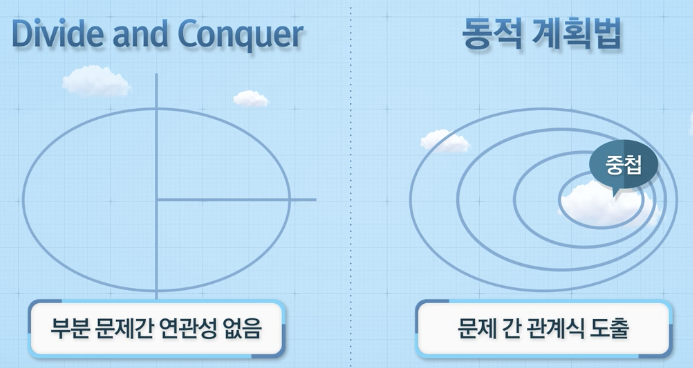
동적 계획법 역사
- 리처드 벨만, 1950년도 제안
- 여러 단계에 걸쳐 순차적으로 의사결정
- 다단계(multistage) 혹은 순차적(sequential) 의사결정 프로세스
- 1950년대 프로그래밍 의미: Planning
--> Dynamic Programming 제안

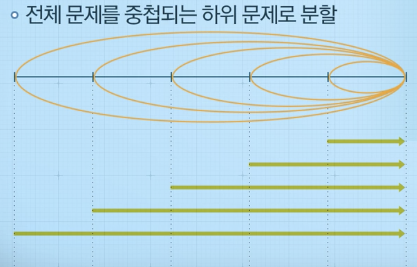
- 하위 단계부터 순차적으로 문제 해결하여 최종 문제를 해결
2-2. 동적 계획법의 주요 개념(1) 최적화의 원리
동적 계획법 적용 선행조건
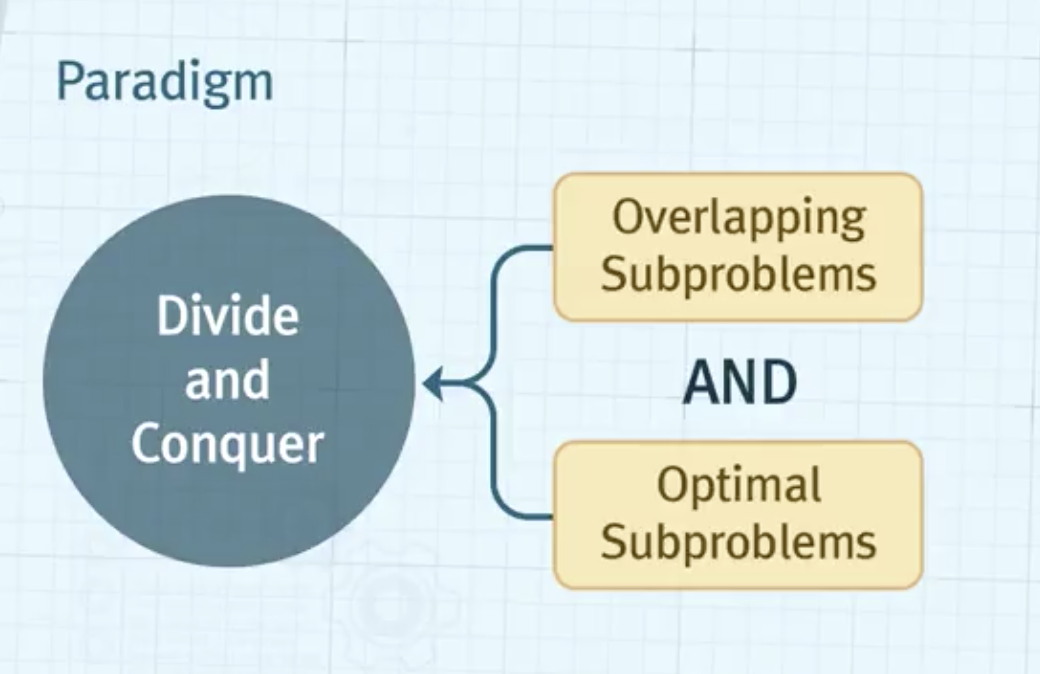
- Overlapping Subproblems
- 중첩되는 부분 문제의 구조를 가져야 함
- 부분 문제 및 상위 부분 문제의 형태 동일
- 다만, 문제의 크기만 변화
==> 실질적 문제의 형태는 동일한 형태 - 해결하고자 하는 문제 정의 필요
ex.
- Optimal substructure (최적 부분 구조)
- 한 문제의 최적해는 그 부분 문제의 최적해들로부터 구성이 된다
- 재귀적인 구조를 통해서 문제를 해결해 나가기 위해 반드시 선행되어야 하는 조건
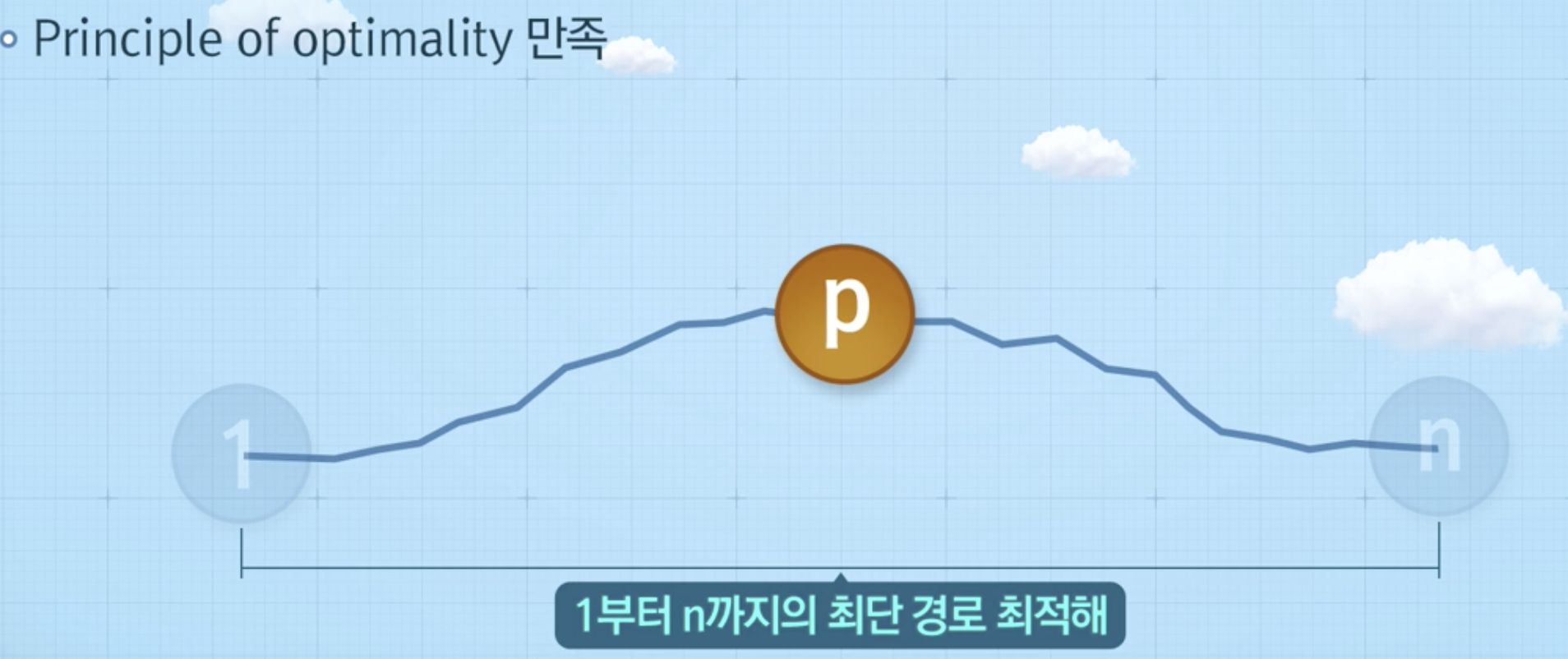
최적화의 원리 (Principle of Optimality)
- 리처드벨만: 한 문제에 대한 해가 최적이라면 그 문제를 이루는 모든 부분문제들에 해당하는 부분해가 부분문제의 최적해
최단 경로 문제
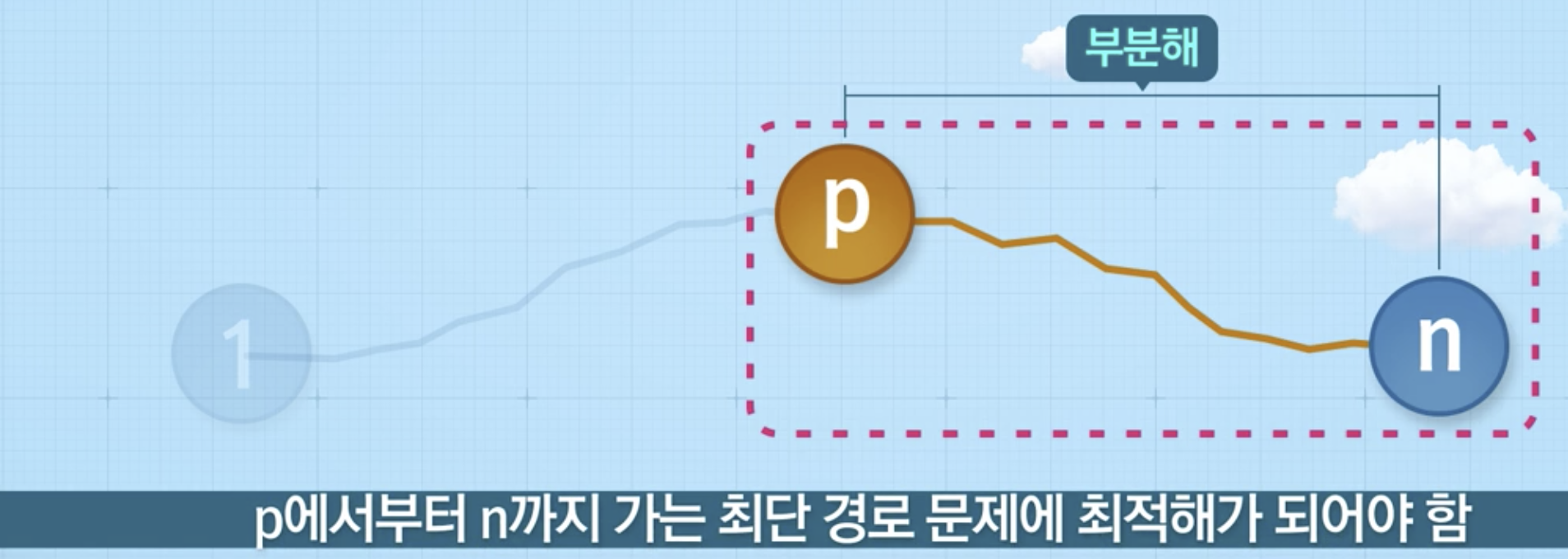
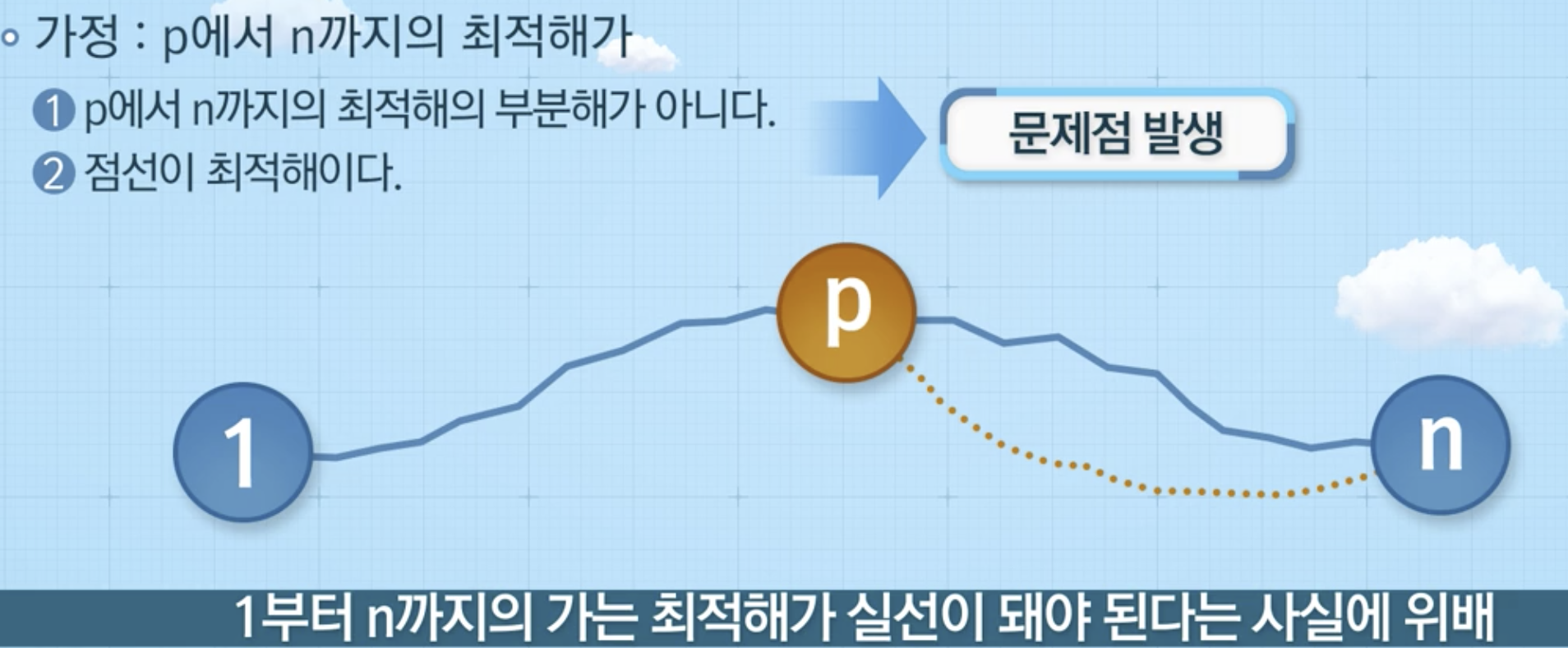
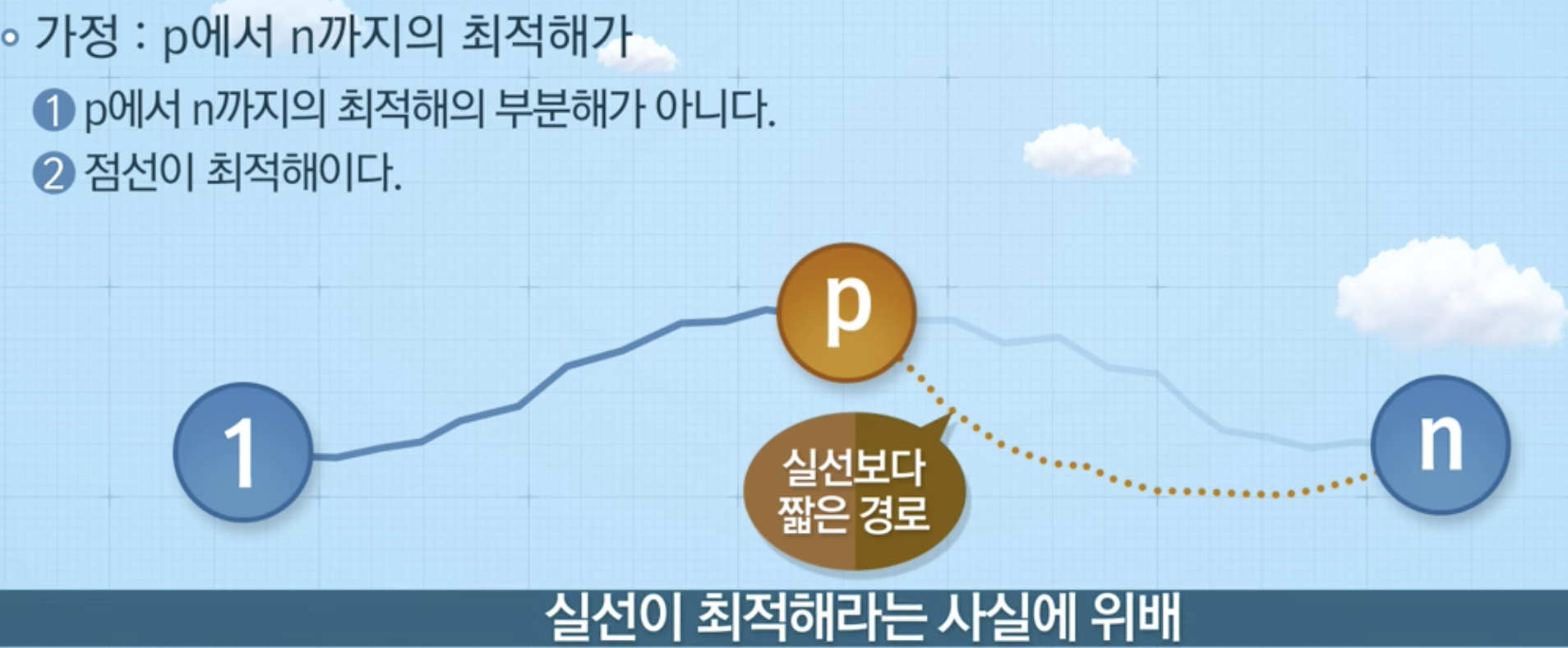
최장 경로 문제 (Longest path problem)
-
특정 노드의 중복 방문을 허용하지 않으면서 가장 거리가 먼 경로를 찾는 문제

-
1-->3까지 가는 부분 문제의 최장 경로
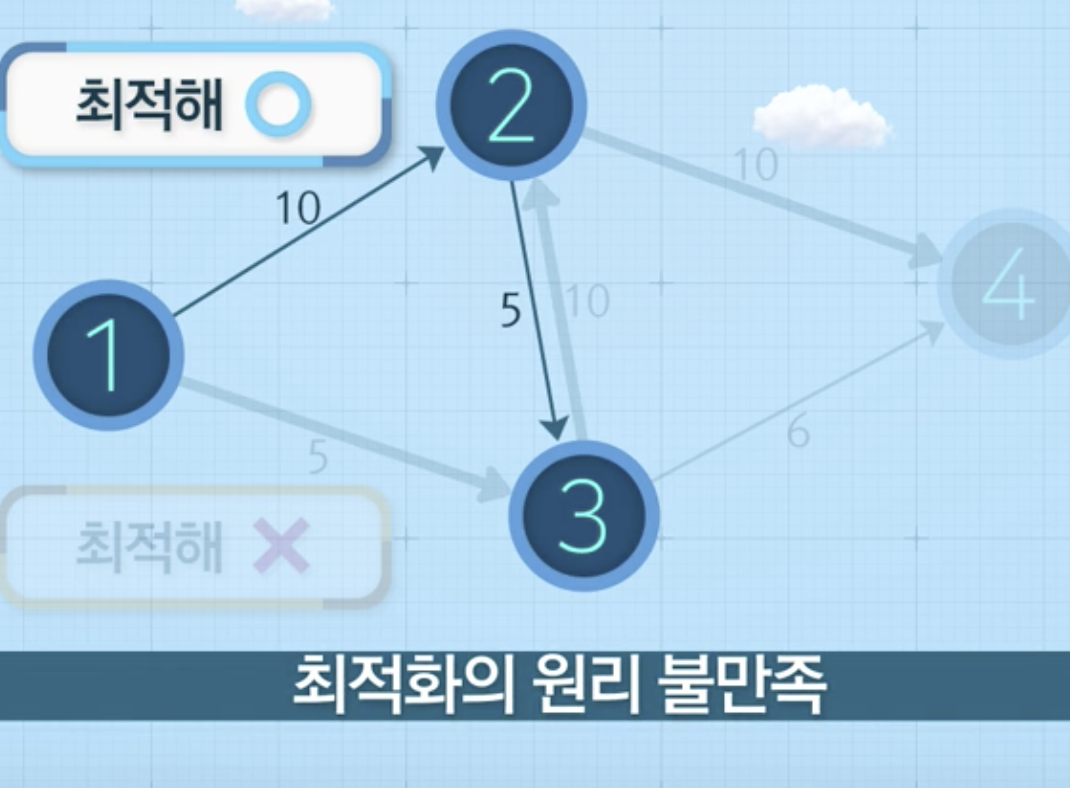
최장 경로 문제는 동적 계획법으로 해결 불가능한가?
- 문제를 다른 방식으로 재정의
- 문제에 추가 정보 도입 및 재정의
- 최적화의 원리를 만족할 수 있는 문제 구조로 재구조화
--> Principle of optimality 불만족 문제도 동적 계획법으로 해결 가능
2-3. 동적 계획법의 주요 개념(2) 중첩되는 부분문제와 역진귀납법
순차적 의사결정 문제 예시
문제 상황

- : 매달 시작일 자본 수준
- : t번째 달 사용한 돈의 양
- : 남은 돈의 양
- : 다음 달 초기자본 수준
- : t 기간 동안의 총 효용 (utility)
- 효용함수 정의:
- 가정: 돈을 사용한 만큼 만족도 비례 증가
풀이 방법
- 상황
- 사용해야 하는 돈의 수준은 소유 자본에 제약
- 에 따라 자본 수준 결정
- 이전 단계 의사결정에 따라 결정
--> 전 단계 의사결정이 이후 수준 의사결정에 영향
- 모든 경우의 수 찾기는 어려움
- 중첩되는 문제구조 구성 필요
- 동적 계획법 형태로 문제 구조화
문제 구조
- 가정: t시점에 만큼 자본 수준 보유
- 남은 기간 동안 의사결정
- 이전 단계 의사결정에 영향 받지 않음 (=독립성을 가진다)
- 과거와는 t시점에 만큼의 자본수준을 보유한다는 사실에만 의존
--> 만큼 자본 보유
--> 독립적인 의사결정
문제 구조화
- 함수 정의
- 시점에서의 자본수준이 x일 때,
t시점부터 남은 기간 동안의 총 효용의 최대값 - : 초기 상태부터 남은 기간 동안에 얻을 수 있는 총 효용의 최대값
- 시점에서의 자본수준이 x일 때,
- 값 계산을 위한 가장 하위 문제는?
- 이전 경로 문제 예시: 우측 하단에서 목적지 >> 목적지
- : 마지막 달의 총효용의 최대값
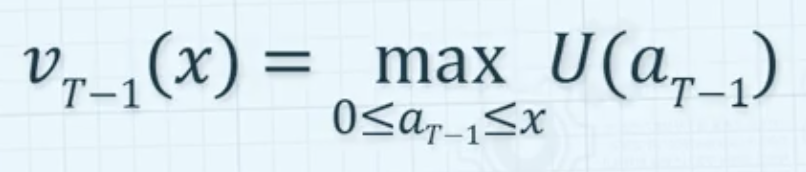
- : t-1시점의 자본수준이 x일 경우, (효용 최대화를 위해) 얼마만큼 지출할 것인지 알려주는 함수
- : 마지막 달 자본수준이 x일 경우, x만큼 돈 사용시, 총 효용이 최대화됨

- : 마지막 달 자본수준이 x일 경우, x만큼 돈 사용시, 총 효용이 최대화됨
남은 두 기간 동안 총 효용 최대화

- 문제 재정의: 어떤 a를 선택해야 총 요용을 최대화할 수 있을까?
- v라는 subproblem과 재귀적 형태로 문제 재정의
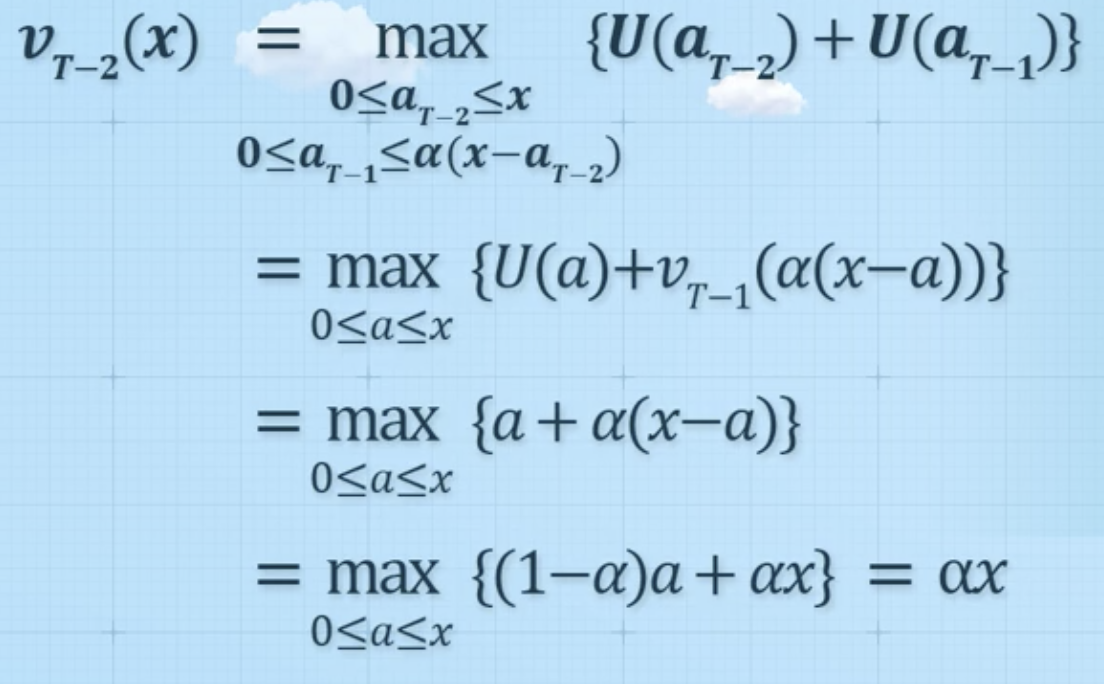
- t-2시점 자본수준이 x일 때, 남은 두 기간 총 효용 최대값
- v라는 subproblem과 재귀적 형태로 문제 재정의
함수값 도출 (의사결정 규칙)

(확정적)동적 계획법
개념
- 순차적 의사결정
- 의사결정을 내리는 시점: 단계(stages), 의사결정시점(decision epoch)
- 의사결정을 내릴 때 필요한 정보: 상태(state)
- 상태(state)를 바탕으로 의사결정: 행동(action)
- 상태: 각 달에 보유한 자본 수준
- 행동: 돈 사용량
- 돈 사용량 결정 --> 다음 달 초기자본 수준 결정
확정적 동적 계획법
- 정의: 어떤 상태에서 어떤 액션 결정 시, 그 다음 단계의 상태가 확정적으로 결정됨
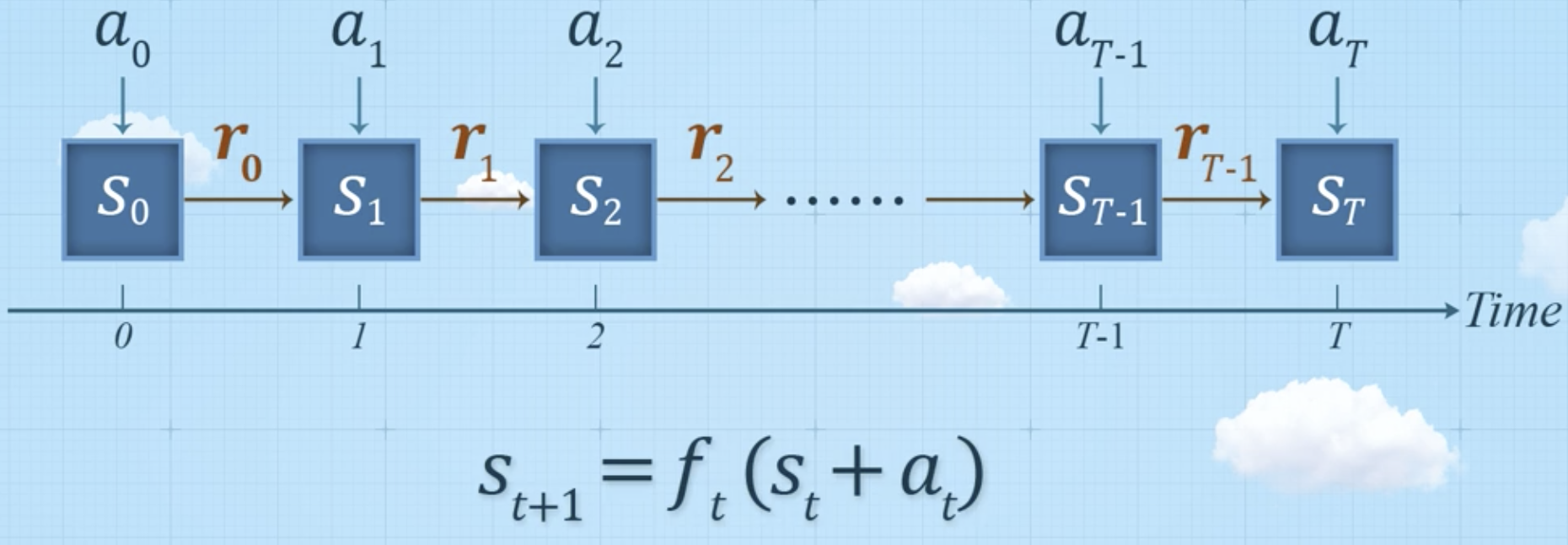
- 의사결정을 하고자 하는 평가지표 필요
- 동적계획법: 각 단계에 해당하는 보상 개념 도입
어떤 상태에서 어떤 행동 --> 보상
이전 단계 문제
- 만큼 돈 사용
- 만큼 효용 발생
--> 보상의 개념과 대비
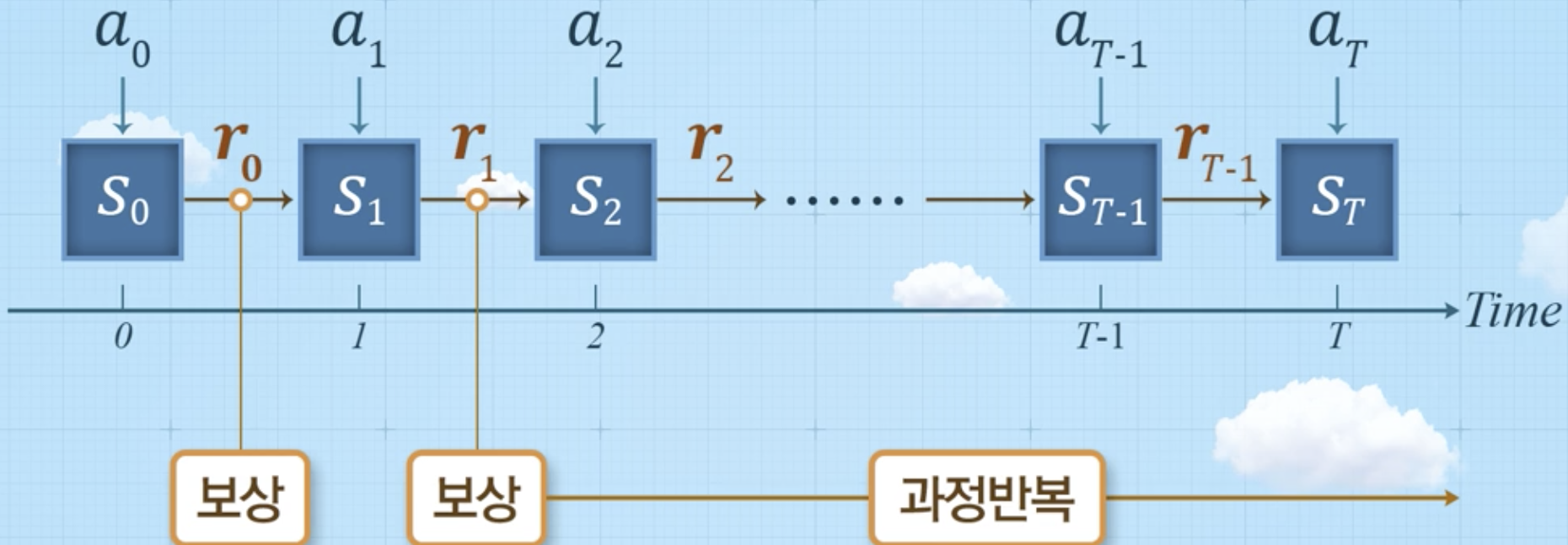
a결정 시 활용하는 평가지표
- 어떤 평가기준을 가지고 각 단계에서 a라는 의사결정을 내릴 것인가?

- Decision rule
- 각 단계에서 모든 가능한 상태에 대해, 상태 별 의사결정 해야 할 행동을 정의한 함수
- 정책 (Policy)
- 모든 단계에서의 decision rule의 집합
하위 문제 정의
- 특정 단계에서의 한 상태 가정
- 이후 남은 단계들에서 이뤄진 모든 의사결정은 현 단계 이전의 의사결정에 영향을 주지 않음 --> 독립성 유지
- 이후 의사결정들은 이전 의사결정들에 당연히 영향을 받음
- But 특정 단계에서 상태 정보가 명확하다면, 상태 정보 주어진 시점부터 이후 의사결정은 어느 상태에 도달했다는 정보로 충분함
정의

중첩되는 부분문제들 (overlapping subproblems)
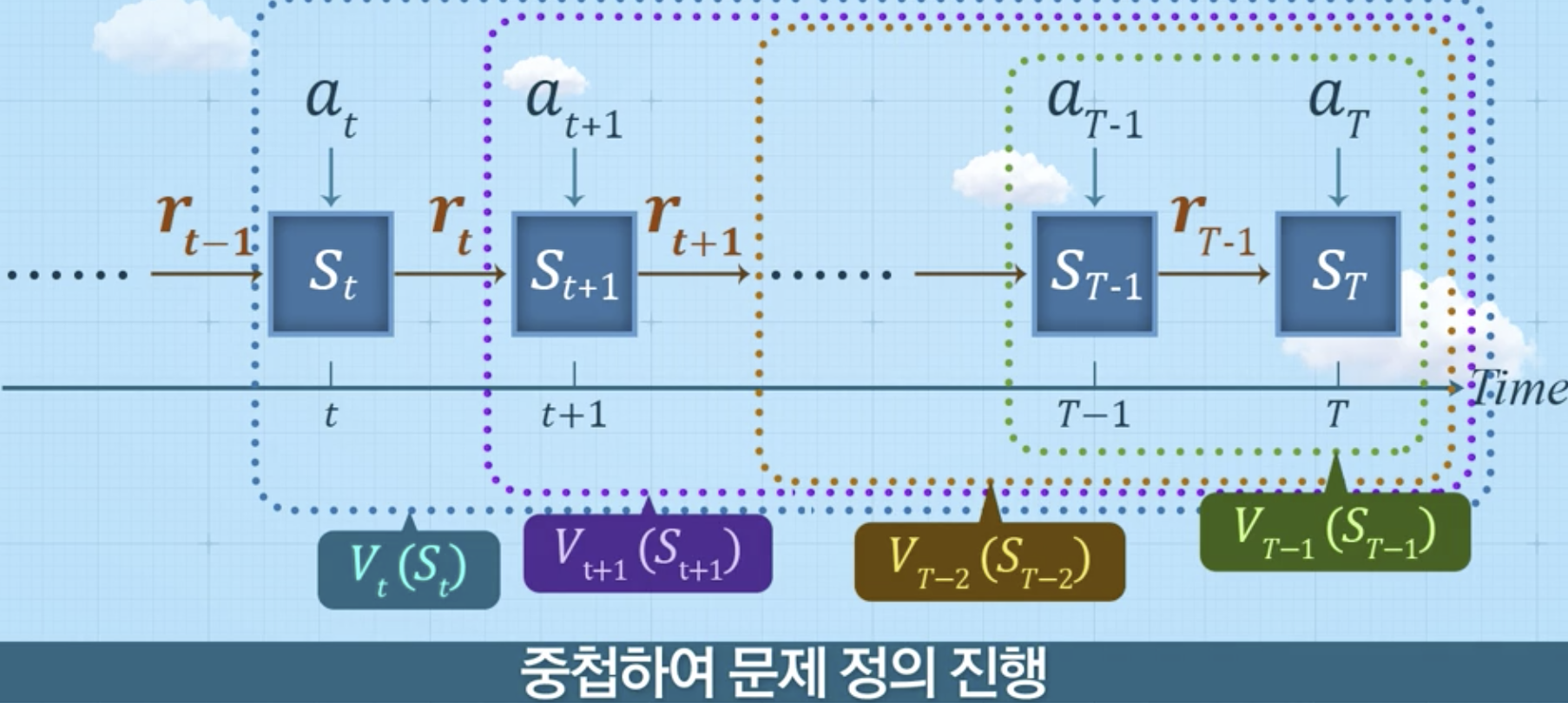
벨만 최적 방정식 (Bellman Optimality Equation)
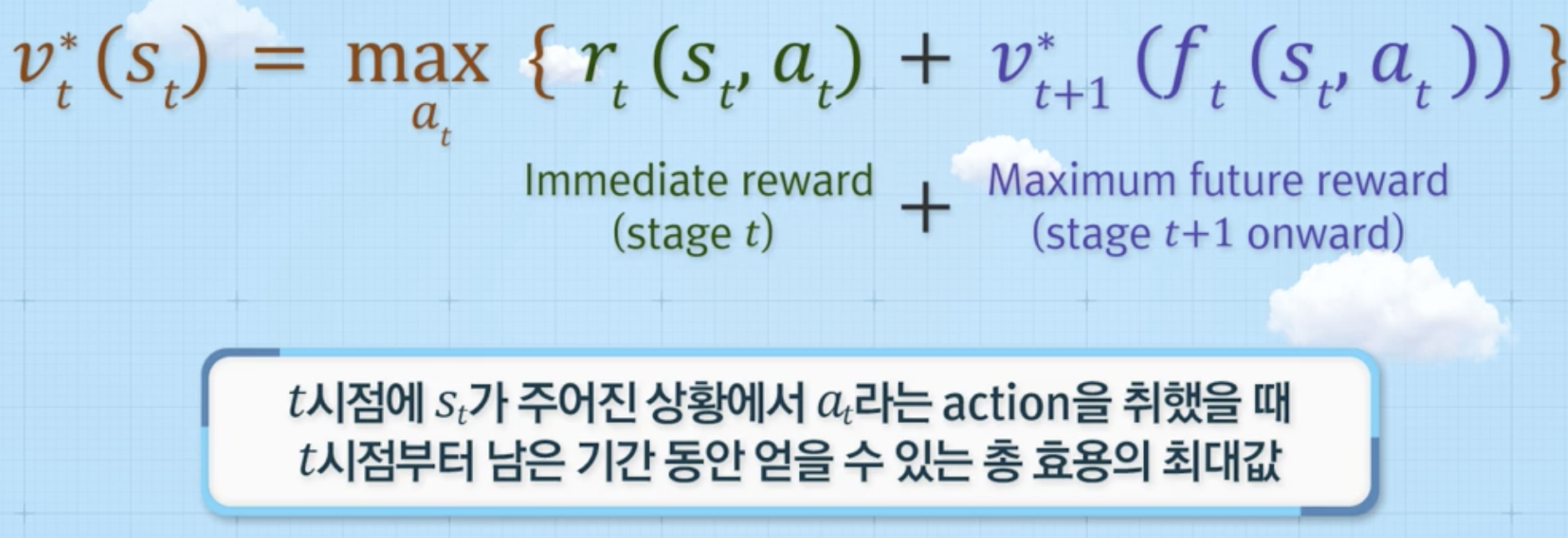


역진 귀납법
- Backward induction
- 작은 크기의 문제부터 순차적으로 풀어나감
- 가장 마지막 단계부터 순차적 문제 해결

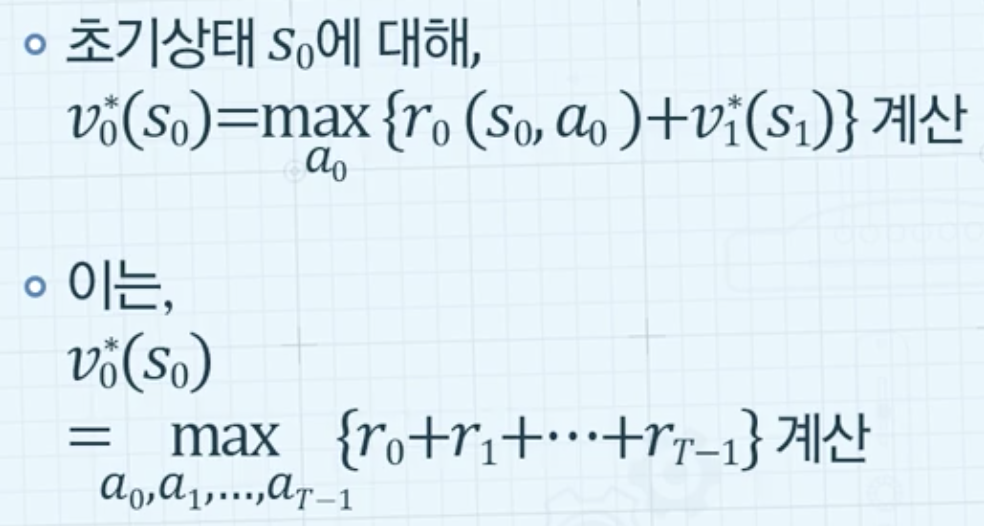
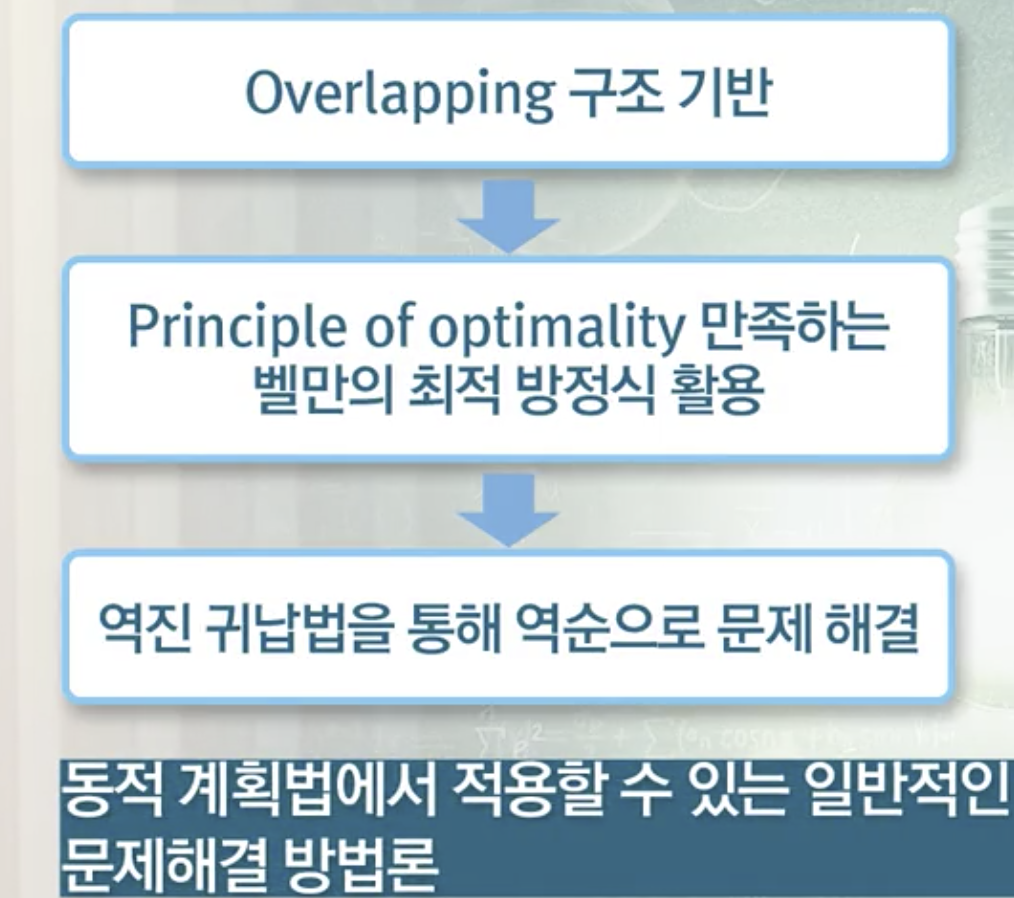
동적 계획법의 일반적인 문제해결 방법론