[백준]1850번 : 최대공약수

📌 출처

1850번 : 최대공약수

📝 문제

모든 자리가 1로만 이루어져있는 두 자연수 A와 B가 주어진다. 이때, A와 B의 최대 공약수를 구하는 프로그램을 작성하시오.

예를 들어, A가 111이고, B가 1111인 경우에 A와 B의 최대공약수는 1이고, A가 111이고, B가 111111인 경우에는 최대공약수가 111이다.

⌨ 입력

첫째 줄에 두 자연수 A와 B를 이루는 1의 개수가 주어진다. 입력되는 수는 263보다 작은 자연수이다.

🖨 출력

첫째 줄에 A와 B의 최대공약수를 출력한다. 정답은 천만 자리를 넘지 않는다.

💻 내 코드

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        long num1 = sc.nextLong();
        long num2 = sc.nextLong();

        long gcd = getGCD(num1, num2);

        StringBuilder sb = new StringBuilder();
        for(int i=1; i <= gcd; i++) {
            sb.append("1");
        }

        System.out.println(sb);

    }

    public static long getGCD(long a, long b) {
        while(b > 0) {
            long tmp = a;
            a = b;
            b = tmp%b;
        }
        return a;
    }
}

✏ 설명

처음에는 주어진 입력을 1111, 111111과 같이 숫자로 만들어놓고 최대공약수를 구하려고 하였으나 범위가 너무 커질 것 같아 포기하였다.
결국 입력과 출력 사이의 규칙을 찾기로 하였다.
주어진 예시 외에도 몇 가지 예시를 생각해보다 찾은 규칙은 다음과 같다.

• 주어진 두 입력의 최대공약수와 출력의 1의 개수가 같다.

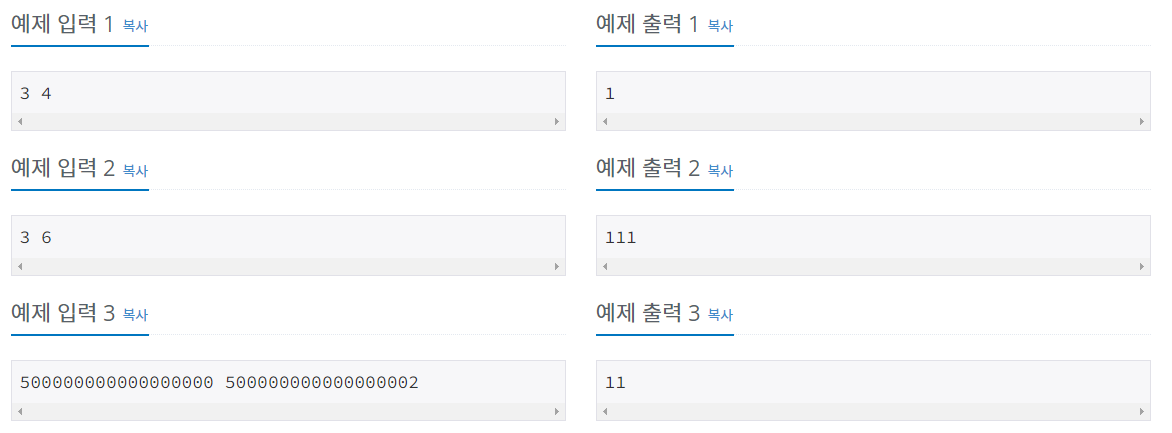
3과 4의 최대공약수는 1 => 출력 1
3과 6의 최대공약수는 3 => 출력 111
500000000000000000과 500000000000000002의 최대공약수는 2 => 출력 2
6과 15의 최대공약수는 3 => 출력 111

결국 두 입력의 최대공약수를 찾은 후 그 개수만큼 1을 쓰면 되는 것이다.

이렇게 규칙은 찾았지만 다음으로 마주한 문제는 최대공약수를 구하는 방법이었다.
최대공약수의 경우 유클리드 호제법을 사용하여 문제를 해결한다.

• 유클리드 호제법 과정
  1. 큰 수(A)를 작은 수(B)로 나눈다.
  2. 나누는 수(B)를 나머지(C)로 나눈다.
  3. 나누는 수(C)를 나머지(D)로 또 나눈다.
  4. 나머지가 0이 될 때까지 이를 반복한다.
  5. 나머지가 0이 나오면 그 때 나눴던 수가 최대공약수이다.

어떻게 진행되는지는 알겠는데 왜 그게 최대공약수가 되는지 이해가 되지 않아서 원리를 찾아봤다.

• 유클리드 호제법 이해하기
  1. 어떤 수 $A$를 $B$로 나눈다면 다음과 같이 표현한다.
     $A=B*Q+R$
  2. 이 때 A와 B의 최대공약수를 $G$라고 했을 때 $A=a*G, B=b*G$로 나타낼 수 있고 위 식에 대입해 $R$에 대해 정리하면 다음과 같이 표현할 수 있다.
     $a*G=b*G*Q+R$
     $R=a*G-b*G*Q=G*(a-b*Q)$
  3. 즉 나머지 $R$도 최대공약수($G$)를 갖고 있으니 $B$와 $R$의 최대공약수가 곧 $A$와 $B$의 최대공약수를 구하는 것과 동일하다.