Sec2: Traversing & Simulation(String, 1Dim, 2Dim List Traversing
01_회문 문자열 검사
1) Problem
N개의 문자열 데이터를 입력받아 앞에서 읽을 때나 뒤에서 읽을 때나 같은 경우(회문 문자열)이면 YES를 출력하고
회문 문자열이 아니면 NO를 출력하는 프로그램을 작성한다.
단, 회문을 검사할 때 대소문자를 구분하지 않습니다.
입력설명 :
첫 줄에 정수 N(1<=N<=20)이 주어지고, 그 다음 줄부터 N개의 단어가 입력된다.
각 단어의 길이는 100을 넘지 않는다.
출력설명 :
각 줄에 해당 문자열의 결과를 YES 또는 NO로 출력한다.
입력예제 1
5
level
moon
abcba
soon
gooG
출력예제 1
#1 YES
#2 NO
#3 YES
#4 NO
#5 YES
2) Thinking
검사할 문자열 개수 입력받기
첫 번째 문자열 입력받기
대문자 변경
문자열 길이가 5라면 가운데 글자 제외 맨 앞글자 맨 뒷글자 같은 지 검사하는 메커니즘
아니면 문자열을 뒤부터 인덱싱한 문자열이 원래의 문자열과 같은지 확인하는 메커니즘도 가능
다르다면 No 출력, else Yes 출력
3) 선수 지식 : String Indexing
s = '123456789abcd'
print(s[::-1])
print(s[4:1:-1]) # 4 ~ 2
print(s[:0:-1]) # ~ 1
print(s[::-2])dcba987654321
543
dcba98765432
db975314) Lec Sol
N = int(input())
for i in range(N):
s = input()
s = s.upper()
size = len(s)
for j in range(size // 2):
if s[j] != s[-1-j]:
print(f'#{i + 1} NO')
break
else:
print(f'#{i + 1} YES')2
level
#1 YES
good
#2 NO5) Lec Sol#2
N = int(input())
for i in range(N):
s = input()
s = s.upper()
if s == s[::-1]:
print(f'#{i + 1} YES')
else:
print(f'#{i + 1} NO')2
level
#1 YES
good
#2 NO02_숫자만 추출해서 약수의 개수 구하기
1) Problem
문자와 숫자가 섞여있는 문자열이 주어지면 그 중 숫자만 추출하여 그 순서대로 자연수를 만듭니다.
만들어진 자연수와 그 자연수의 약수 개수를 출력합니다.
만약 “t0e0a1c2h0er”에서 숫자만 추출하면 0, 0, 1, 2, 0이고 이것을 자연수를 만들면 120이 됩니다.
즉, 첫자리 0은 자연수화 할 때 무시합니다.
출력은 120를 출력하고, 다음 줄에 120의 약수의 개수를 출력하면 됩니다.
추출하여 만들어지는 자연수는 100000000을 넘지 않습니다.
입력설명 :
첫 줄에 숫자가 썩인 문자열이 주어집니다. 문자열의 길이는 50을 넘지 않습니다.
출력설명 :
첫 줄에 자연수를 출력하고, 두 번째 줄에 약수의 개수를 출력합니다.
입력예제 1
g0en2Ts8eSoft
출력예제 1
28
6
2) Thinking
숫자와 문자가 무작위로 섞인 문자열을 입력받기
isdecimal을 이용하여 숫자만 골라 하나의 수 만들기
그 수의 약수의 개수 세기
3) Lec Sol
s = input()
res = 0
for x in s:
if x.isdecimal():
res = res * 10 + int(x)
print(res)
for i in range(1, res + 1):
if res % i == 0:
cnt += 1
print(cnt)g0en2Ts8eSoft
28
64) GPT Sol
s = input()
numbers = []
for x in s:
if x.isdigit():
numbers.append(int(x))
number_str = ''.join(map(str, numbers))
# print(number_str) # 028
res = int(number_str)
cnt = 0
for i in range(1, res + 1):
if res % i == 0:
cnt += 1
print(res)
print(cnt)g0en2Ts8eSoft
28
603_카드 역배치
1) Problem
1부터 20까지 숫자가 하나씩 쓰인 20장의 카드가 아래 그림과 같이 오름차순으로 한 줄로 놓여있다.
각 카드의 위치는 카드 위에 적힌 숫자와 같이 1부터 20까지로 나타낸다.
 이제 여러분은 다음과 같은 규칙으로 카드의 위치를 바꾼다 :
이제 여러분은 다음과 같은 규칙으로 카드의 위치를 바꾼다 :
구간 [a, b] (단, 1 ≤ a ≤ b ≤ 20)가 주어지면 위치 a부터 위치 b까지의 카드를 현재의 역순으로 놓는다.
예를 들어, 현재 카드가 놓인 순서가 위의 그림과 같고 구간이 [5, 10]으로 주어진다면,
위치 5부터 위치 10까지의 카드 5, 6, 7, 8, 9, 10을 역순으로 하여 10, 9, 8, 7, 6, 5로 놓는다.
이제 전체 카드가 놓인 순서는 아래 그림과 같다.
 이 상태에서 구간 [9, 13]이 다시 주어진다면,
이 상태에서 구간 [9, 13]이 다시 주어진다면,
위치 9부터 위치 13까지의 카드 6, 5, 11, 12, 13을 역순으로 하여 13, 12, 11, 5, 6으로 놓는다.
이제 전체 카드가 놓인 순서는 아래 그림과 같다.
 오름차순으로 한 줄로 놓여있는 20장의 카드에 대해 10개의 구간이 주어지면,
오름차순으로 한 줄로 놓여있는 20장의 카드에 대해 10개의 구간이 주어지면,
주어진 구간의 순서대로 위의 규칙에 따라 순서를 뒤집는 작업을 연속해서
처리한 뒤 마지막 카드들의 배치를 구하는 프로그램을 작성하시오.
입력설명 :
총 10개의 줄에 걸쳐 한 줄에 하나씩 10개의 구간이 주어진다.
i번째 줄에는 i번째 구간의 시 작 위치 ai와 끝 위치 bi가 차례대로 주어진다.
이때 두 값의 범위는 1 ≤ ai ≤ bi ≤ 20이다.
출력설명 :
1부터 20까지 오름차순으로 놓인 카드들에 대해,
입력으로 주어진 10개의 구간 순서대로 뒤집는 작업을 했을 때 마지막 카드들의 배치를 한 줄에 출력한다.
입력예제 1
5 10
9 13
1 2
3 4
5 6
1 2
3 4
5 6
1 20
1 20
출력예제 1
1 2 3 4 10 9 8 7 13 12 11 5 6 14 15 16 17 18 19 20
2) Lec Sol
alist = list(range(21))
N = int(input())
for _ in range(N):
s, e = map(int, input().split())
for i in range((e - s + 1) // 2):
alist[s + i], alist[e - i] = alist[e - i], alist[s + i]
alist.pop(0)
for x in alist:
print(x, end = ' ')2
3 8
9 13
1 2 8 7 6 5 4 3 13 12 11 10 9 14 15 16 17 18 19 20 3) GPT Sol
def reverse_list(alist, s, e):
alist[s - 1:e] = reversed(alist[s - 1:e])
return alist
alist = list(range(1, 21))
N = int(input())
for _ in range(N):
s, e = map(int, input().split())
alist = reverse_list(alist, s, e)
print(alist)
# 1
# 2 5
# 1 5 4 3 2 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20분석
[1, 2, 3, 4, 5, 6, 7, 8, ....] value
[0, 1, 2, 3, 4, 5, 6, 7, ....] index
s = 2, e = 5
list[s - 1:e] > list[1:5] > index 1 ~ 4 > value 2 ~ 504_오름차순이 유지된 두 리스트 합치기
1) Problem
Quiz 4
두 리스트 합치기
오름차순으로 정렬이 된 두 리스트가 주어지면 두 리스트를 오름차순으로 합쳐 출력하는 프로그램을 작성하세요.
입력설명 :
첫 번째 줄에 첫 번째 리스트의 크기 N(1<=N<=100)이 주어집니다.
두 번째 줄에 N개의 리스트 원소가 오름차순으로 주어집니다.
세 번째 줄에 두 번째 리스트의 크기 M(1<=M<=100)이 주어집니다.
네 번째 줄에 M개의 리스트 원소가 오름차순으로 주어집니다.
각 리스트의 원소는 int형 변수의 크기를 넘지 않습니다.
출력설명 :
오름차순으로 정렬된 리스트를 출력합니다.
입력에제 1
3
1 3 5
5
2 3 6 7 9
출력예제 1
1 2 3 3 5 6 7 9
2) 선수 지식
N개의 리스트를 오름차순으로 정렬하기 위해 sort() 함수를 사용하면
N * logN의 시간복잡도를 갖게된다.
대신 오름차순이 유지된 리스트 두개를 합치는 것은 반복문 N번만 돌면된다.
3) Lec Sol
N = int(input())
alist = list(map(int, input().split()))
M = int(input())
blist = list(map(int, input().split()))
p1 = p2 = 0
clist = []
while p1 < N and p2 < M:
if alist[p1] <= blist[p2]:
clist.append(alist[p1])
p1 += 1
else:
clist.append(blist[p2])
p2 += 1
if p1 < N:
clist = clist + alist[p1:]
if p2 < M:
clist = clist + blist[p2:]
for x in clist:
print(x, end = ' ')3
1 3 5
5
2 3 6 7 9
1 2 3 3 5 6 7 9 05_수들의 합
1) Problem
N개의 수로 된 수열 A[1], A[2], ..., A[N] 이 있다.
이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i + 1] + ... + A[j - 1] + A[j]가
M이 되는 경우의 수를 구하는 프로그램을 작성하시오.
입력설명 :
첫째 줄에 N(1 ≤ N ≤ 10000), M(1 ≤ M ≤ 300000000)이 주어진다.
다음 줄에는 A[1], A[2], ..., A[N]이 공백으로 분리되어 주어진다.
각각의 A[x]는 30000을 넘지 않는 자연수이다.
출력설명 :
첫째 줄에 경우의 수를 출력한다.
입력예제 1
8 3
1 2 1 3 1 1 1 2
출력예제 1
5
2) Thinking
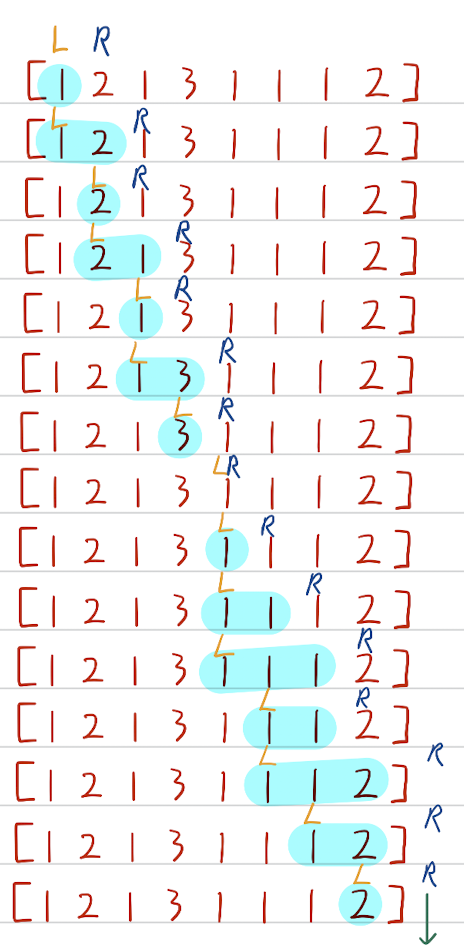 TOT 값에 list의 값을 저장해서 원하는 합보다 작을 때, 같을 때, 클 때로 상황 분류.
TOT 값에 list의 값을 저장해서 원하는 합보다 작을 때, 같을 때, 클 때로 상황 분류.
LT, RT값으로 포인터 역할
LT = 0, RT = 1, TOT = alist[0] = 1
1. 합이 3보다 작으니 alist[RT] 더하고 RT 전진 ㅡ 1
2. 합이 3이니 카운트 후 alist[LT] 빼고 LT 전진 ㅡ 1 2
3. 합이 3보다 작으니 alist[RT] 더하고 RT 전진 ㅡ 2
4. 합이 3이니 카운트 후 alist[LT] 빼고 LT 전진 ㅡ 2 1
5. 합이 3보다 작으니 alist[RT] 더하고 RT 전진 ㅡ 1
6. 합이 3보다 크니 alist[LT] 뺴고 LT 전진 ㅡ 1 3
7. 합이 3이니 카운트 후 alist[LT] 빼고 LT 전진 ㅡ 3
8. 합이 3보다 작으니 alist[RT] 더하고 RT 전진 ㅡ
9. 합이 3보다 작으니 alist[RT] 더하고 RT 전진 ㅡ 1
10. 합이 3보다 작으니 alist[RT] 더하고 RT 전진 ㅡ 1 1
11. 합이 3이니 카운트 후 alist[LT] 빼고 LT 전진 ㅡ 1 1 1
12. 합이 3보다 작으니 alist[RT] 더하고 RT 전진 ㅡ 1 1
13. 합이 3보다 크니 alist[LT] 뺴고 LT 전진 ㅡ 1 1 2
14. 합이 3이니 카운트 후 alist[LT] 빼고 LT 전진 ㅡ 1 2
15. 합이 3보다 작은데 RT 전진 불가, break ㅡ 2
3) Lec Sol
# 인프런 답안
N, M = map(int, input().split())
alist = list(map(int, input().split()))
LT = 0
RT = 1
TOT = alist[0]
cnt = 0
while True:
if TOT < M: # 아직도 합이 3이 안됐을 때
if RT < N: # RT가 앞으로 더 갈 수 있을 때
TOT += alist[RT] # 더하고
RT += 1 # RT 전진
else: # RT 전진이 불가능
break # 반복문 탈출
elif TOT == M: # 합이 3이 됐을 때
cnt += 1 # 카운트
TOT -= alist[LT] # 빼고
LT += 1 # LT 전진
else: # 3보다 작은 것도 아니고 3인 것도 아닌, 3보다 클 때
TOT -= alist[LT] # 빼고
LT += 1 # LT 전진
print(cnt)8 3
1 2 1 3 1 1 1 2
54) GPT Sol
N, M = map(int, input().split())
alist = list(map(int, input().split()))
cnt = 0
for i in range(N):
for j in range(i, N):
if sum(alist[i:j+1]) == M:
cnt += 1
print(cnt)8 3
1 2 1 3 1 1 1 2
506_격자판 최대합
1) Problem
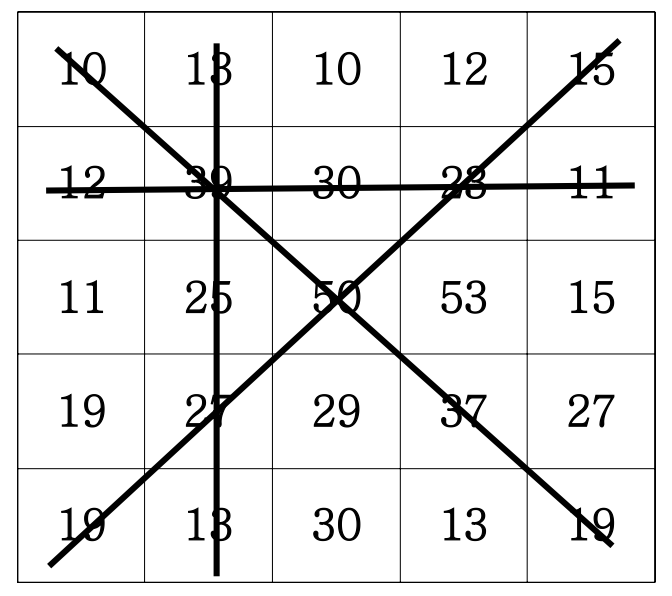
5 5 격자판에 그림과 같이 숫자가 적혀있습니다.
N N의 격자판이 주어지면 각 행의 합, 각 열의 합, 두 대각선의 합 중 가장 큰 합을 출력합니다.
입력설명 :
첫 줄에 자연수 N이 주어진다.(1<=N<=50)
두 번째 줄부터 N줄에 걸쳐 각 줄에 N개의 자연수가 주어진다.
각 자연수는 100을 넘지 않는다.
출력설명 :
최대합을 출력합니다.
입력예제 1
5
10 13 10 12 15
12 39 30 23 11
11 25 50 53 15
19 27 29 37 27
19 13 30 13 19
출력예제 1
155
2) Lec Sol
N = int(input())
alist = [list(map(int, input().split())) for _ in range(N)] # 2차원 배열 생성
max = -2147000000
for i in range(N):
sum1 = sum2 = 0
for j in range(N): # i = 0 일때, j가 다 돌아야 0번째 행과 0번째 열의 합이 각각 계산됨
sum1 += alist[i][j] # 행 고정 후 j(열) 돌리기
sum2 += alist[j][i] # 열 고정 후 j(행) 돌리기
if sum1 > max:
max = sum1
if sum2 > max:
max = sum2
sum1 = sum2 = 0
for i in range(N):
sum1 += alist[i][i] # y = -x
sum2 += alist[i][N - 1 - i] # y = x
if sum1 > max:
max = sum1
if sum2 > max:
max = sum2
print(max)3
1 2 7
1 7 2
7 1 2
213) GPT Sol
# 격자판의 크기 N을 입력받는다.
N = int(input())
# 격자판의 숫자를 입력받아 2차원 리스트로 저장한다.
grid = [list(map(int, input().split())) for _ in range(N)]
# 각 행의 합을 구한다.
row_sums = []
for row in grid:
row_sum = sum(row)
row_sums.append(row_sum)
# 각 열의 합을 구한다.
col_sums = []
for j in range(N):
col_sum = 0
for i in range(N):
col_sum += grid[i][j]
col_sums.append(col_sum)
# 첫 번째 대각선의 합을 구한다.
diag1_sum = 0
for i in range(N):
diag1_sum += grid[i][i]
# 두 번째 대각선의 합을 구한다.
diag2_sum = 0
for i in range(N):
diag2_sum += grid[i][N-i-1]
# 가장 큰 합을 출력한다.
max_sum = max(max(row_sums), max(col_sums), diag1_sum, diag2_sum)
print(max_sum)3
1 2 7
1 7 2
7 1 2
2107_사과나무(다이아몬드)
1) Problem
현수의 농장은 N*N 격자판으로 이루어져 있으며, 각 격자안에는 한 그루의 사과나무가 심어저 있다.
N의 크기는 항상 홀수이다.
가을이 되어 사과를 수확해야 하는데,
현수는 격자판안의 사과를 수확할 때 다이아몬드 모양의 격자판만 수확하고 나머지 격자안의 사과는 새들을 위해서 남겨놓는다.
만약 N이 5이면 아래 그림과 같이 진한 부분의 사과를 수확한다.
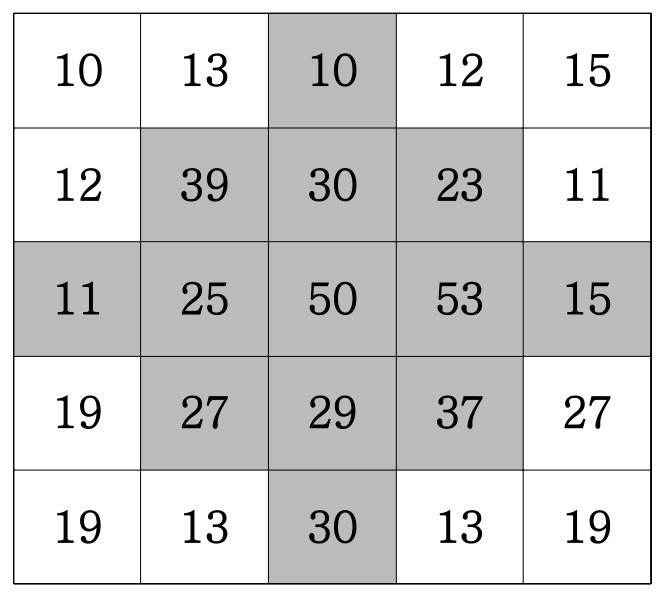 현수과 수확하는 사과의 총 개수를 출력하세요.
현수과 수확하는 사과의 총 개수를 출력하세요.
입력설명 :
첫 줄에 자연수 N(홀수)이 주어진다.(3<=N<=20)
두 번째 줄부터 N줄에 걸쳐 각 줄에 N개의 자연수가 주어진다.
이 자연수는 각 격자안에 있는 사과나무에 열린 사과의 개수이다.
각 격자안의 사과의 개수는 100을 넘지 않는다.
출력설명 :
수확한 사과의 총 개수를 출력합니다.
입력예제 1
5
10 13 10 12 15
12 39 30 23 11
11 25 50 53 15
19 27 29 37 27
19 13 30 13 19
출력예제 1
379
2) Lec Sol
N = int(input())
alist = [list(map(int, input().split())) for _ in range(N)]
res = 0
s = e = N // 2
for i in range(N):
for j in range(s, e + 1):
res += alist[i][j]
if i < N // 2: # 중간 직전 행까지는 범위 확대
s -= 1
e += 1
else: # 범위 축소
s += 1
e -= 1
print(res)5
99 99 10 99 99
99 10 10 10 99
10 10 10 10 10
99 10 10 10 99
99 99 10 99 99
13008_모래시계
1) Problem
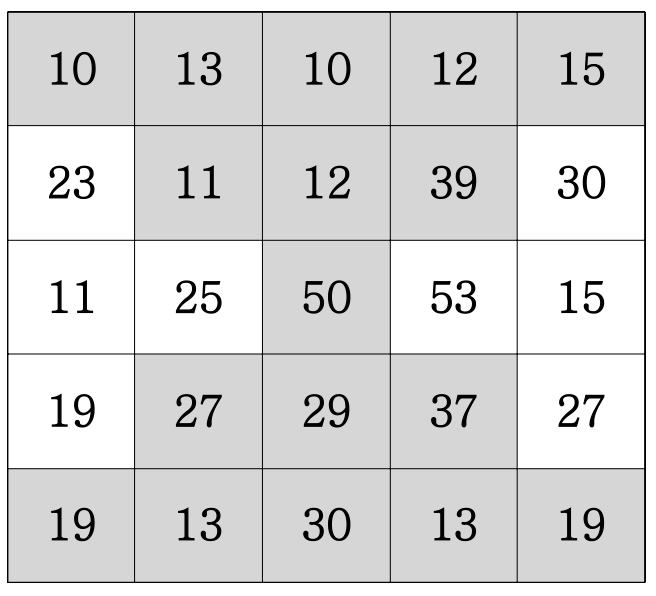
N * N 격자판이 주어진다.
M개의 회전명령 정보를 받는다, 예를 들어 2 0 3이면 2번째 행을 왼쪽으로 3번 회전시킨다.
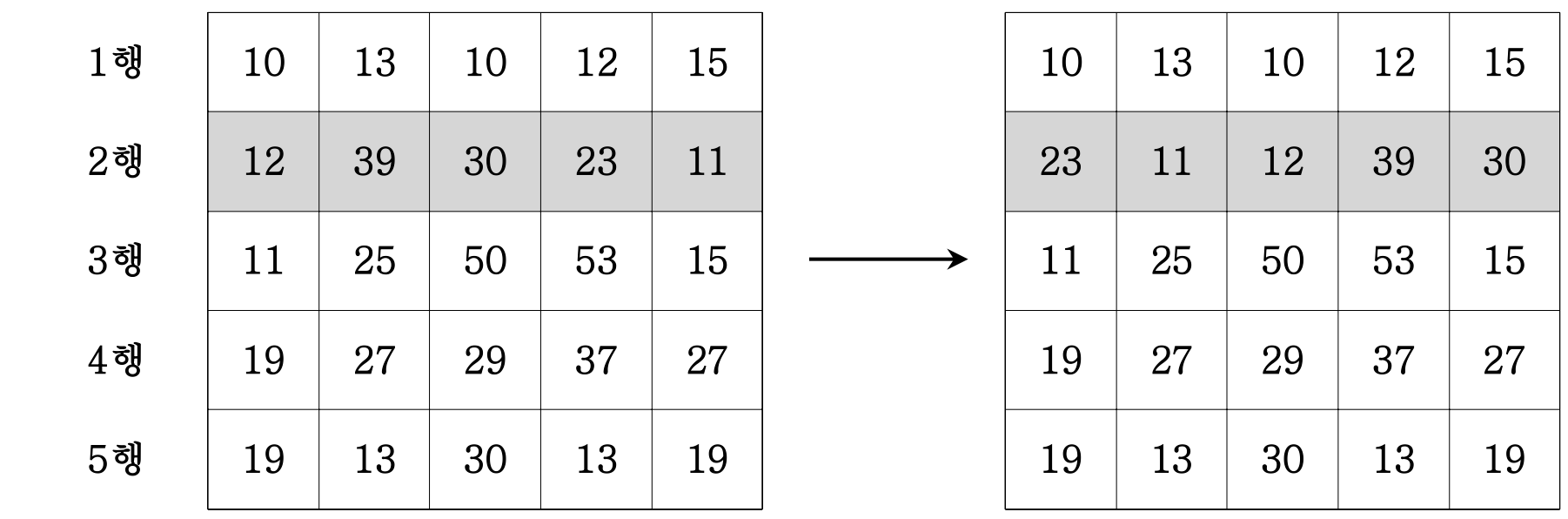
 입력설명 :
입력설명 :
첫 줄에 자연수 N(3<=N<=20) 이 주어지며, N은 홀수입니다.
두 번째 줄부터 N줄에 걸쳐 각 줄에 N개의 자연수가 주어진다.
이 자연수는 각 격자안에 있는 감의 개수이며, 각 격자안의 감의 개수는 100을 넘지 않는다.
그 다음 줄에 회전명령의 개수인 M(1<=M<=10)이 주어지고, 그 다음 줄부터 M개의 회전명령 정보가 M줄에 걸쳐 주어집니다.
출력설명 :
총 감의 개수를 출력합니다.
입력예제 1
5
10 13 10 12 15
12 39 30 23 11
11 25 50 53 15
19 27 29 37 27
19 13 30 13 19
3
2 0 3
5 1 2
3 1 4
출력예제 1
362
2) Lec Sol
N = int(input())
alist = [list(map(int, input().split())) for _ in range(N)]
M = int(input())
for _ in range(M):
R, D, k = map(int, input().split())
if D == 0: # 왼쪽으로 회전
for _ in range(k):
alist[R - 1].append(alist[R - 1].pop(0))
else:
for _ in range(k):
alist[R - 1].insert(0, alist[R - 1].pop())
res = 0
s = 0
e = N - 1
for i in range(N):
for j in range(s, e + 1):
res += alist[i][j]
if i < N // 2:
s += 1
e -= 1
else:
s -= 1
e += 1
print(res)5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
3
2 0 2
4 1 3
5 0 1
5309_봉우리
1) Problem
지도 정보가 N * N 격자판에 주어집니다.
각 격자에는 그 지역의 높이가 쓰여있습니다.
각 격자 판의 숫자 중 자신의 상하좌우 숫자보다 큰 숫자는 봉우리 지역입니다.
봉우리 지역이 몇 개 있는 지 알아내는 프로그램을 작성하세요.
격자의 가장자리는 0으로 초기화 되었다고 가정한다.
만약 N=5 이고, 격자판의 숫자가 다음과 같다면 봉우리의 개수는 10개입니다.
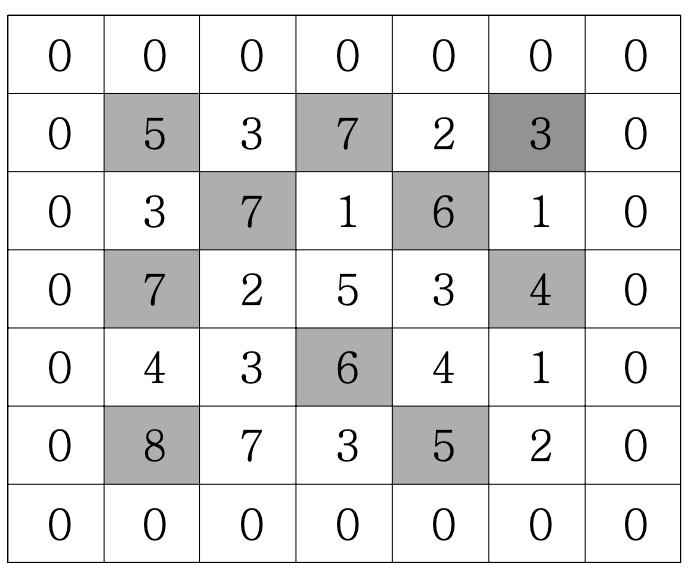 입력설명 :
입력설명 :
첫 줄에 자연수 N이 주어진다.(1<=N<=50)
두 번째 줄부터 N줄에 걸쳐 각 줄에 N개의 자연수가 주어진다.
각 자연수는 100을 넘지 않는다.
출력설명 :
봉우리의 개수를 출력하세요.
입력예제 1
5
5 3 7 2 3
3 7 1 6 1
7 2 5 3 4
4 3 6 4 1
8 7 3 5 2
출력예제 1
10
2) Lec Sol
N = int(input())
alist = [list(map(int, input().split())) for _ in range(N)]
alist.insert(0, [0] * N) # 0으로 채운 첫 번째 행 생성
alist.append([0] * N) # 0으로 채운 마지막 행 생성
for x in alist: # 행마다 앞뒤로 0 추가
x.insert(0, 0)
x.append(0)
dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
# [좌 하 우 상]
cnt = 0
for i in range(1, N + 1):
for j in range(1, N + 1):
if all(alist[i][j] > alist[i + dx[k]][j + dy[k]] for k in range(4)): # 상하좌우 탐색
cnt += 1
print(cnt)3
2 1 2
1 2 1
2 1 2
510_스도쿠 검사
1) Problem
스도쿠는 매우 간단한 숫자 퍼즐이다.
9 × 9 크기의 보드가 있을 때, 각 행과 각 열,
그리고 9개의 3 × 3 크기의 보드에 1부터 9까지의 숫자가 중복 없이 나타나도록 보드를 채우면 된다.
예를 들어 다음을 보자.
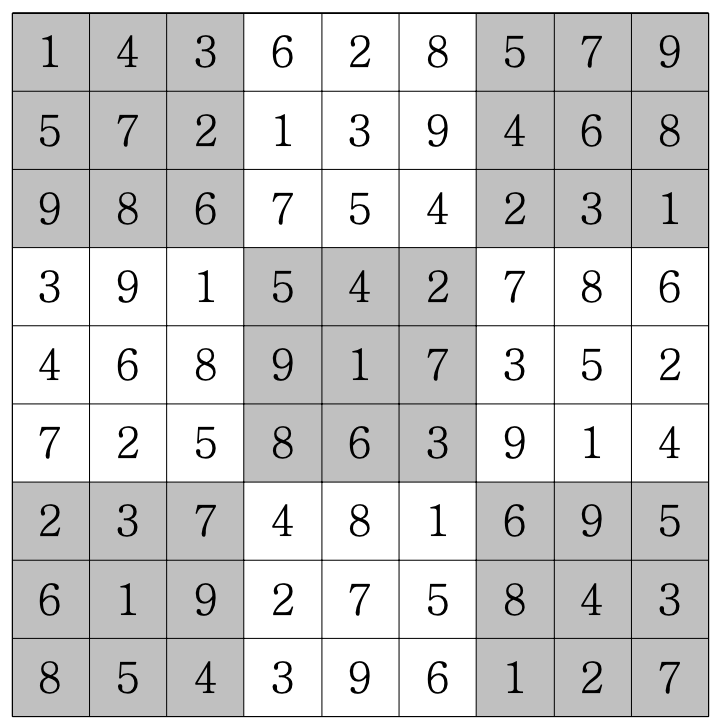 위 그림은 스도쿠를 정확하게 푼 경우이다.
위 그림은 스도쿠를 정확하게 푼 경우이다.
각 행에 1부터 9까지의 숫자가 중복 없이 나오고, 각 열에 1부터 9까지의 숫자가 중복 없이 나오고,
각 3 × 3짜리 사각형(9개이며, 위에서 색깔로 표시되었다)에 1부터 9까지의 숫자가 중복 없이 나오기 때문이다.
완성된 9 × 9 크기의 수도쿠가 주어지면 정확하게 풀었으면 YES, 잘못 풀었으면 NO를 출력하는 프로그램을 작성하세요.
입력설명 :
첫 번째 줄에 완성된 9 x 9 스도쿠가 주어집니다.
출력설명 :
첫째 줄에 YES 또는 NO를 출력하세요.
입력예제 1
1 4 3 6 2 8 5 7 9
5 7 2 1 3 9 4 6 8
9 8 6 7 5 4 2 3 1
3 9 1 5 4 2 7 8 6
4 6 8 9 1 7 3 5 2
7 2 5 8 6 3 9 1 4
2 3 7 4 8 1 6 9 5
6 1 9 2 7 5 8 4 3
8 5 4 3 9 6 1 2 7
출력예제 1
YES
2) Thinking
중복을 확인할 리스트가 3개 필요 : 행, 열, 그룹
체크리스트를 따로 만들어서 1을 할당.
중요한 점은 입력한 리스트의 실제 값을 인덱스로 이용하여 체크리스트에 1을 할당하는 것.
sum으로 체크리스트를 확인하면 9가 나와야 한다.
아닌 경우에는 1이 덮어씌워진 것.(중복할당)
그룹 탐색은 4중 for문을 사용
첫 이중 for문은 그룹 9개를 3by3인 2차원 리스트로 보는 것이고
그룹을 선택한 후에 두 번째 이중 for문으로 체크리스트에 1을 할당한다.
3) Lec Sol
def check(x):
for i in range(9): # 행렬 탐색
ch_row = [0] * 10 # 다음 행, 다음 열 탐색 시작과 함께 체크리스트 초기화
ch_col = [0] * 10
for j in range(9): # 체크리스트에 실제 리스트 값으로 인덱싱
ch_row[alist[i][j]] = 1
ch_col[alist[j][i]] = 1
if sum(ch_row) != 9 or sum(ch_col) != 9: # 행 하나 열 하나 검사
return False
for i in range(3): # 그룹 9개로 나눠 3by3 리스트로 보기
for j in range(3):
ch_group = [0] * 10 # 그룹마다 체크리스트 초기화
for k in range(3): # 그룹 내 행렬 탐색
for s in range(3):
ch_group[alist[i*3+k][j*3+s]] = 1
if sum(ch_group) != 9:
return False
return True
alist = [list(map(int, input().split())) for _ in range(9)]
if check(alist):
print('YES')
else:
print('NO')1 4 3 6 2 8 5 7 9
5 7 2 1 3 9 4 6 8
9 8 6 7 5 4 2 3 1
3 9 1 5 4 2 7 8 6
4 6 8 9 1 7 3 5 2
7 2 5 8 6 3 9 1 4
2 3 7 4 8 1 6 9 5
6 1 9 2 7 5 8 4 3
8 5 4 3 9 6 1 2 7
YES11_격자판 회문수
1) Problem
1부터 9까지의 자연수로 채워진 7 * 7 격자판이 주어지면
격자판 위에서 가로방향 또는 세로방향으로 길이 5자리 회문수가 몇 개 있는지 구하는 프로그램을 작성하세요.
회문수란 121과 같이 앞에서부터 읽으나 뒤에서부터 읽으나 같은 수를 말합니다.
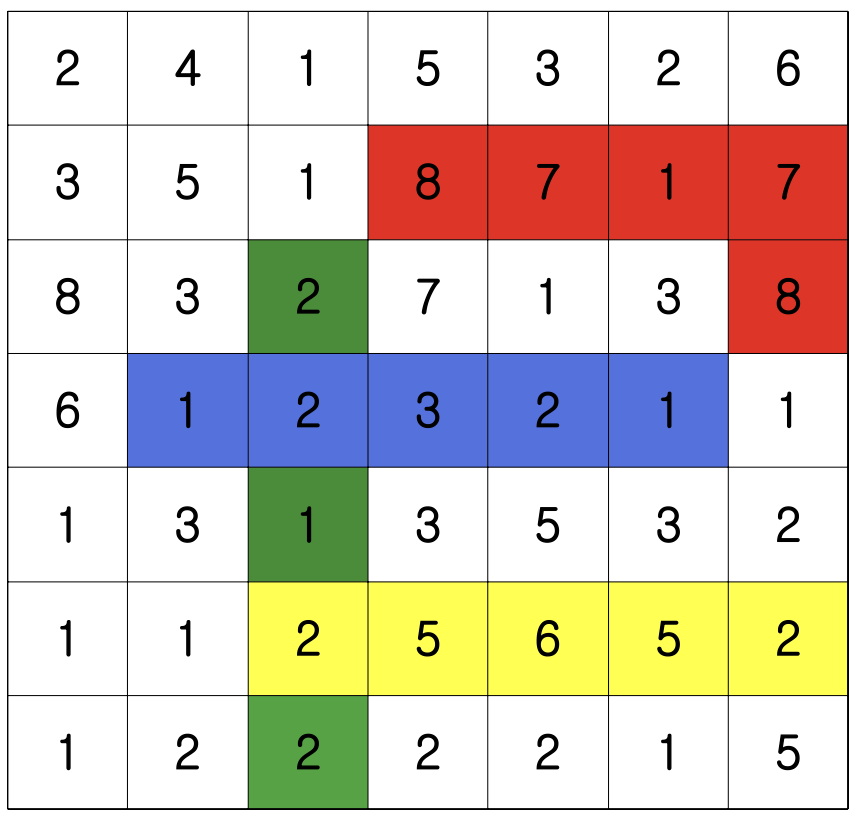 빨간색처럼 구부러진 경우(87178)는 회문수로 간주하지 않습니다.
빨간색처럼 구부러진 경우(87178)는 회문수로 간주하지 않습니다.
입력설명 :
1부터 9까지의 자연수로 채워진 격자판 7 * 7 격자판이 주어집니다.
출력설명 :
5자리 회문수의 개수를 출력합니다.
입력예제 1
2 4 1 5 3 2 6
3 5 1 8 7 1 7
8 3 2 7 1 3 8
6 1 2 3 2 1 1
1 3 1 3 5 3 2
1 1 2 5 6 5 2
1 2 2 2 2 1 5
출력예제 1
3
2) Thinking
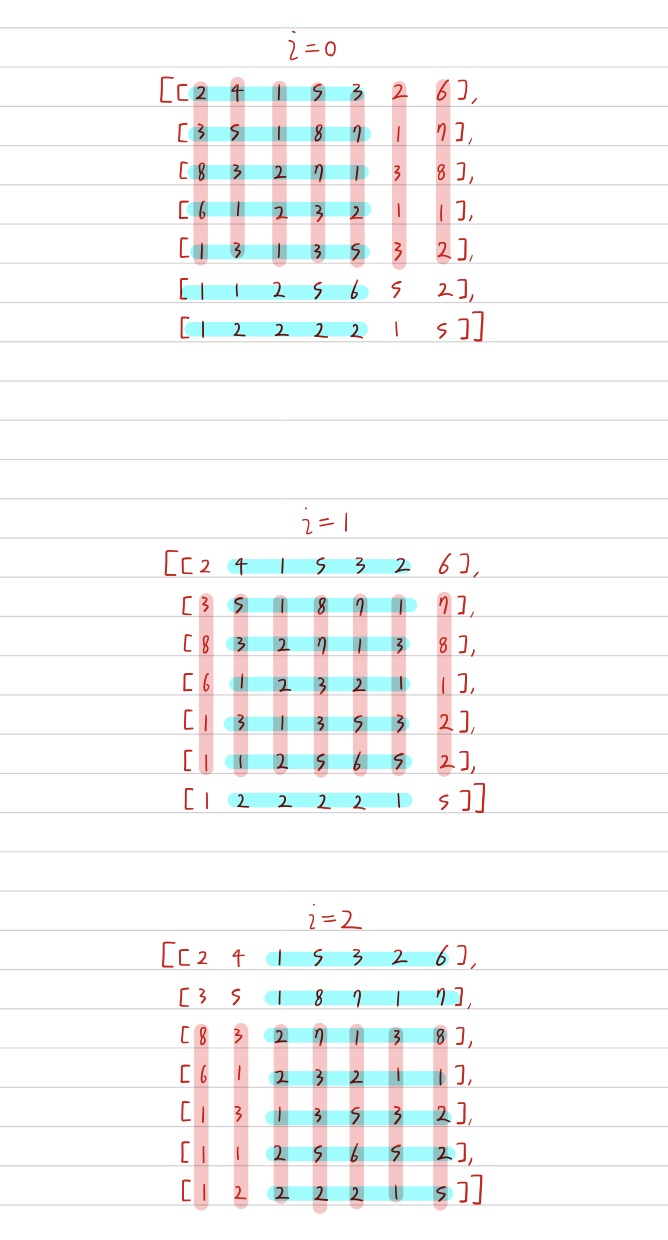
i = 0 > list[i:i+5] > j 탐색(0~6)
j 탐색하면서 k(0~2)로 열 탐색
i = 1 > list[i:i+5] > j 탐색(0~6)
j 탐색하면서 k(0~2)로 열 탐색
i = 2 > list[i:i+5] > j 탐색(0~6)
j 탐색하면서 k(0~2)로 열 탐색
3) Lec Sol
alist = [list(map(int, input().split())) for _ in range(7)]
cnt = 0
for i in range(3):
for j in range(7):
five = five[j][i:i+5] # 행 탐색, 열 고정 > i값이 동일할 때 j로 행 조정
if five == five[::-1]:
cnt += 1
for k in range(2): # 열 탐색, 행 고정 > i값이 동일할 때 k로 행 조정, j로 열 조정 / k돌고 if 만족 안하면 else로
if alist[i+k][j] != alist[i+4-k][j]:
break
else:
cnt += 1
print(cnt)2 4 1 5 3 2 6
3 5 1 8 7 1 7
8 3 2 7 1 3 8
6 1 2 3 2 1 1
1 3 1 3 5 3 2
1 1 2 5 6 5 2
1 2 2 2 2 1 5
34) Lec Sol#2
alist = [list(map(int, input().split())) for _ in range(7)]
cnt = 0
for i in range(3):
for j in range(7):
if alist[j][i:i+5] == alist[j][i:i+5][::-1]:
cnt += 1
for i in range(7):
for j in range(3):
tmp = []
for k in range(5):
tmp.append(alist[j+k][i])
if tmp == tmp[::-1]:
cnt += 1
print(cnt)2 4 1 5 3 2 6
3 5 1 8 7 1 7
8 3 2 7 1 3 8
6 1 2 3 2 1 1
1 3 1 3 5 3 2
1 1 2 5 6 5 2
1 2 2 2 2 1 5
3
