최단 경로 알고리즘

1. 다익스트라
2. 예제

1. 다익스트라

그래프에서 여러 노드가 있을 때, 특정 노드에서 다른 노드로 가는 최단 경로를 구하는 알고리즘이다. 기본적으로 그리디 알고리즘으로 분류되는데, 매번 가장 비용이 적은 노드를 선택하는 과정을 수행한다. 현재 가장 가까운 노드를 저장하기 위해서 우선순위 큐를 사용한다.

heapq는 튜플 입력을 받으면 첫 번째 원소를 기준으로 우선순위 큐를 정렬하므로 (거리: xx, 노드: xx) 형태로 유선 순위 큐에 집어넣는다.

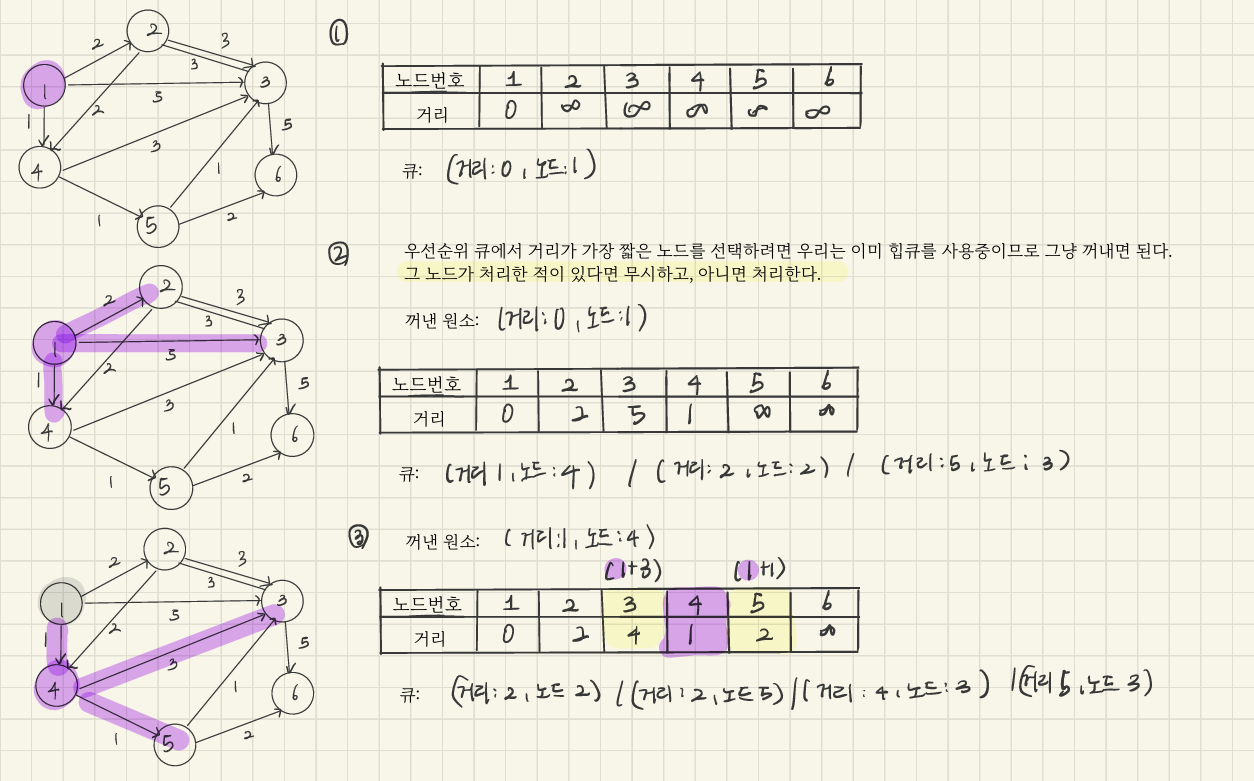
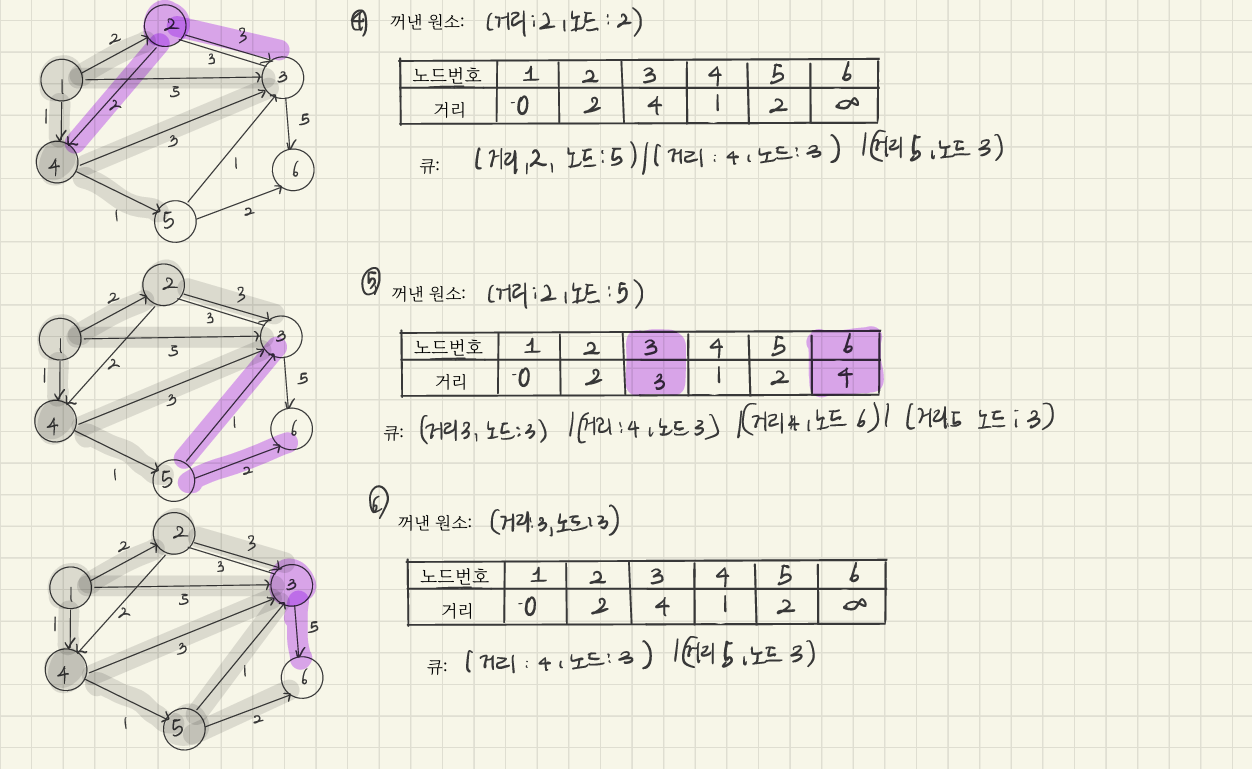
이런 식으로 최단 경로를 업데이트 해주면 된다.

데이터 수가 N 개 일 때, 하나의 데이터를 삽입 및 삭제 할 때 시간 복잡도는 O(logN) 이다.

🐥 코드

import heapq
import sys
input=sys.stdin.readline
INF=int(1e9)

#노드의 개수, 간선의 개수
n,m=map(int,input().split())
#시작 노드
start=int(input())
#각 노드에 연결되어 있는 노드의 정보를 담은 리스트
graph=[[] for i in range(n+1)]
#최단 거리 테이블 초기화
distance=[INF]*(n+1)

for _ in range(m):
    a,b,c=map(int,input().split())
    #a->b까지 비용:c
    graph[a].append((b,c))

def dijkstra(start):
    q=[]
    heapq.heappush(q,(0,start))
    distance[start]=0
    while q:
        dist,now=heapq.heappop(q)
        #현재 노드가 이미 처리된 적이 있는 노드라면
        if distance[now]<dist:
            continue
        #현재 노드와 연결된 다른 인접한 노드들 확인
        for i in graph[now]:
            cost=dist+i[1]
            #현재 노드를 거치는 것이 더 짧을 경우
            if cost<distance[i[0]]:
                distance[i[0]]=cost
                heapq.heappush(q,(cost,i[0]))

dijkstra(start)
print(distance)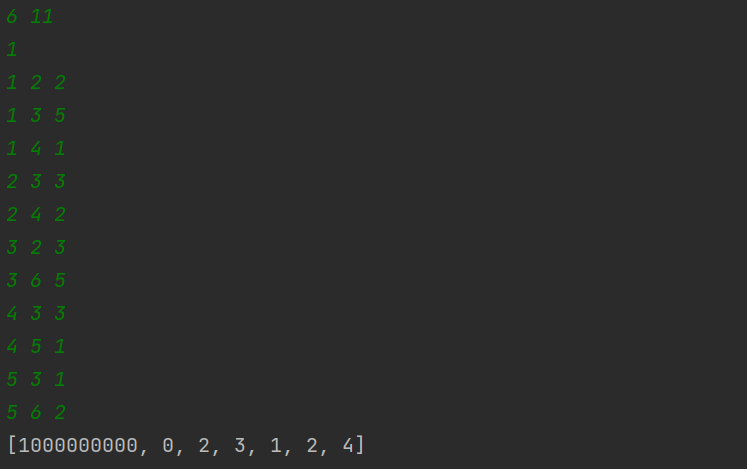

---

2. 예제

어떤 나라에는 N개의 도시가 있다.

그리고 각 도시는 보내고자 하는 메시지가 있는 경우, 다른 도시로 전보를 보내서 다른 도시로 해당 메시지를 전송할 수 있다. 하지만 X라는 도시에서 Y라는 도시로 전보를 보내고자 한다면, 도시 X에서 Y로 향하는 통로가 설치되어 있어야 한다. 예를 들어 X에서 Y로 향하는 통로는 있지만, Y에서 X로 향하는 통로가 없다면 Y는 X로 메시지를 보낼 수 없다. 또한 통로를 거쳐 메시지를 보낼 때는 일정 시간이 소요된다.

어느 날 C라는 도시에서 위급 상황이 발생했다. 그래서 최대한 많은 도시로 메시지를 보내고자 한다. 메시지는 도시 C에서 출발하여 각 도시 사이에 설치된 통로를 거쳐, 최대한 많이 퍼져나갈 것이다. 각 도시의 번호와 통로가 설치되어 있는 정보가 주어졌을 때, 도시 C에서 보낸 메시지를 받게 되는 도시의 개수는 총 몇 개이며 도시들이 모두 메시지를 받는 데까지 걸리는 시간은 얼마인지 계산하는 프로그램을 작성하시오.

• 입력 조건

첫째 줄에 도시의 개수 N, 통로의 개수 M, 메시지를 보내고자 하는 도시 C가 주어진다. (1 ≤ N ≤ 30,000, 1 ≤ M ≤ 200,000, 1 ≤ C ≤ N)
둘째 줄부터 M+1번째 줄에 걸쳐서 통로에 대한 정보 X, Y, Z가 주어진다. 이는 특정 도시 X에서 다른 특정 도시 Y로 이어지는 통로가 있으며, 메시지가 전달되는 시간이 Z라는 의미다. (1 ≤ X, Y ≤ N, 1 ≤ Z ≤ 1,000)

• 출력 조건

첫째 줄에 도시 C에서 보낸 메시지를 받는 도시의 총 개수와 총 걸리는 시간을 공백으로 구분하여 출력한다.

import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)

N, M, C = map(int, input().split())
graph = [[] for i in range(N+1)]
distance = [INF] * (N+1)

for i in range(M):
    x, y, z = map(int, input().split())
    graph[x].append((y, z))



def dijkstra(start):
    q = []
    heapq.heappush(q, (0, start))
    distance[start] = 0
    while q:
        dist, now = heapq.heappop(q)
        if distance[now] < dist:
            continue
        for i in graph[now]:
            cost = dist + i[1]
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(q, (cost, i[0]))

dijkstra(C)

# 도달할 수 있는 노드의 개수
city = 0
# 도달할 수 있는 노드 중에서, 가장 멀리 있는 노드와의 최단 거리
max_distance = 0

for d in distance:
    # 도달할 수 있는 노드인 경우
    if d != INF:
        city += 1
        max_distance = max(max_distance, d)

# 시작 노드는 제외해야 하므로 city - 1을 출력
print(city - 1, max_distance)