정렬

1. 버블 정렬 (Bubble sort)

1) 개념

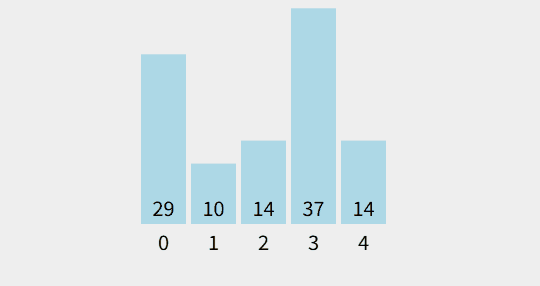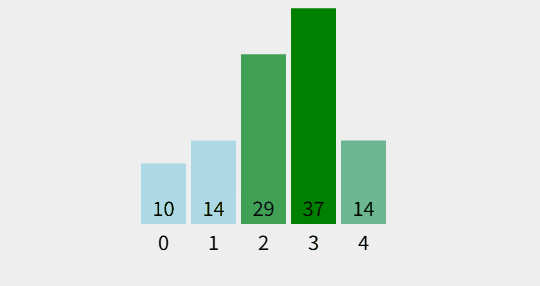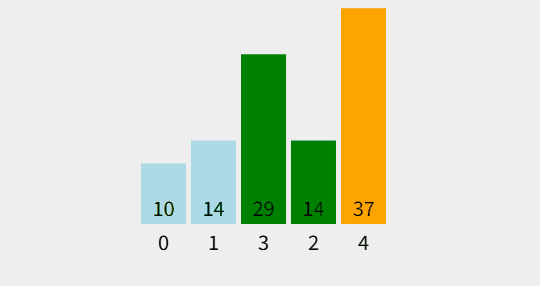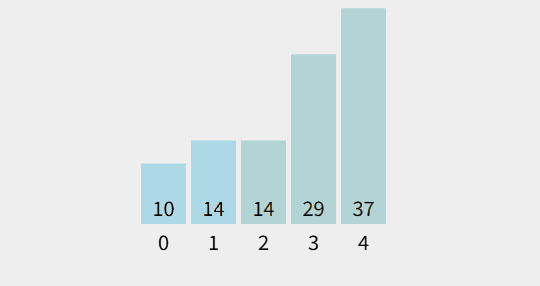
출처 : visualgo.net

• 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어진 이름이다
• 자신의 옆 원소와 대소비교 및 정렬
• Stable, In-place 정렬
• $O(N^2)$

2) 의사코드 및 구현 코드

bubble_sort(A[1..N]) { # A[1..N]을 오름차순 정렬한다.
    for last <- N downto 2 
        for i <- 1 to last - 1 
            if (A[i] > A[i + 1]) then A[i] <-> A[i + 1]  # 원소 교환
}

2. 삽입 정렬 (Insertion sort)

1) 개념

출처 : visualgo.net

• 정렬되지 않은 영역의 원소를 선택해서 정렬된 영역의 원소들과 비교후 적절한 위치에 삽입
• Stable, In-place 정렬
• $O(N^2), O(N)$

2) 의사코드 및 구현 코드

insertion_sort(A[1..N]) { # A[1..N]을 오름차순 정렬한다.
    for i <- 2 to N {
        loc = i - 1;
        newItem = A[i];

        # 이 지점에서 A[1..i-1]은 이미 정렬되어 있는 상태
        while (1 <= loc and newItem < A[loc]) {
            A[loc + 1] <- A[loc];
            loc--;
        }
        if (loc + 1 != i) then A[loc + 1] = newItem;
}

3. 선택 정렬 (Selection sort)

1) 개념 (오름차순 기준 설명)

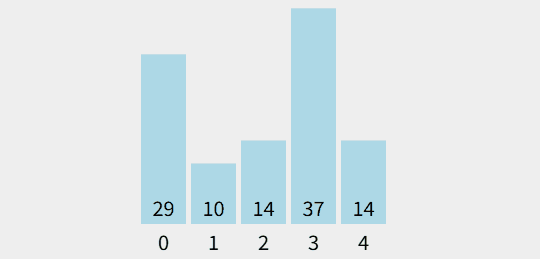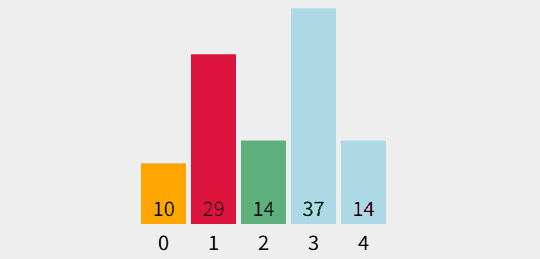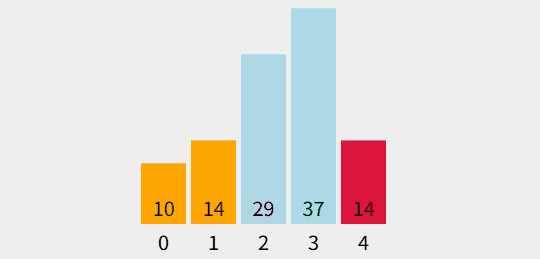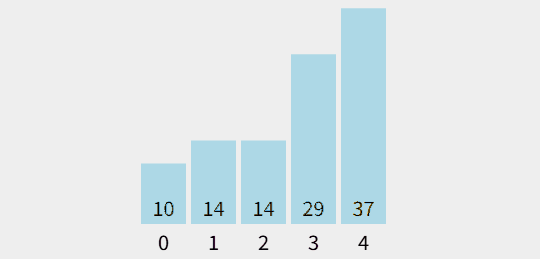
출처 : visualgo.net

• 정렬되지 않은 영역에서 최솟값을 찾아서 정렬된 정렬되지 않은 영역의 처음과 원소 교환
• In-place
• $O(N^2)$

2) 의사코드 및 구현 코드

selection_sort(A[1..N]) { # A[1..N]을 오름차순 정렬한다.
    for first <- 1 to N - 1 {
        A[first..N]중 가장 작은 수 A[i]를 찾는다
        if (first != i) then A[first] <-> A[i]  # first i가 서로 다르면 A[first]와 A[i]를 교환
    }
}

4. 합병 정렬 (Merger sort)

1) 개념

출처 : visualgo.net

• 분할 정복 알고리즘 (Dvide and Conquer)
  • 원소가 1개일 때까지 분할
  • 원소를 합치며 정렬
• 추가적인 메모리가 필요함
• $O(NlogN)$

2) 의사코드 및 구현 코드

merge_sort(A[p..r]) { # A[p..r]을 오름차순 정렬한다.
    if (p < r) then {
        q <- ⌊(p + r) / 2⌋;       # q는 p, r의 중간 지점
        merge_sort(A, p, q);      # 전반부 정렬
        merge_sort(A, q + 1, r);  # 후반부 정렬
        merge(A, p, q, r);        # 병합
    }
}

#A[p..q]와 A[q+1..r]을 병합하여 A[p..r]을 오름차순 정렬된 상태로 만든다.
#A[p..q]와 A[q+1..r]은 이미 오름차순으로 정렬되어 있다.
merge(A[], p, q, r) {
    i <- p; j <- q + 1; t <- 1;
    while (i ≤ q and j ≤ r) {
        if (A[i] ≤ A[j])
        then tmp[t++] <- A[i++]; # tmp[t] <- A[i]; t++; i++;
        else tmp[t++] <- A[j++]; # tmp[t] <- A[j]; t++; j++;
    }
    while (i ≤ q)  # 왼쪽 배열 부분이 남은 경우
        tmp[t++] <- A[i++];
    while (j ≤ r)  # 오른쪽 배열 부분이 남은 경우
        tmp[t++] <- A[j++];
    i <- p; t <- 1;
    while (i ≤ r)  # 결과를 A[p..r]에 저장
        A[i++] <- tmp[t++]; 

5. 힙 소트 (heap sort)

1) 개념

출처 : wikimedia.org/wikipedia

• heap 자료구조를 사용한 정렬
• heap을 생성하면 원소들은 논리적인 정렬상태, 실제 컨테이너가 정렬된 것이 아님.
• heap의 원소가 없을 때까지 반복
• heap의 root와 마지막원소 스왑
  • 마지막 위치는 정렬된 것으로봄
  • 바뀐 root부터 max_heapify(root) 실행
• $O(NlogN)$

2) 의사코드 및 구현 코드

heap_sort(A[1..n]) { # A[1..n]을 정렬한다.
    build_min_heap(A, n);
    for i <- n downto 2 {
        A[1] <-> A[i];  # 원소 교환
        heapify(A, 1, i - 1);
    }
}

build_min_heap(A[], n) {
    for i <- ⌊n / 2⌋ downto 1
        heapify(A, i, n)
}

#A[k]를 루트로 하는 트리를 최소 힙 성질을 만족하도록 수정한다.
#A[k]의 두 자식을 루트로 하는 서브 트리는 최소 힙 성질을 만족하고 있다.
#n은 배열 A의 전체 크기이며 최대 인덱스를 나타낸다.
heapify(A[], k, n) {
    left <- 2k; right <- 2k + 1;
    if (right ≤ n) then {
        if (A[left] < A[right]) then smaller <- left;
                                else smaller <- right;
    }
    else if (left ≤ n) then smaller <- left;
    else return;

    # 최소 힙 성질을 만족하지 못하는 경우 재귀적으로 수정한다.
    if (A[smaller] < A[k]) then {
        A[k] <-> A[smaller];
        heapify(A, smaller, n);
    }
}

6. 퀵 소트 (Quick sort)

1) 개념

출처 : visualgo.net

• pivot을 설정하고 이를 기준으로 정렬
• pivot의 좌우 영역에 대해서도 새로운 pivot을 설정해 위의 과정을 반복
• In-place 정렬
• $O(N^2), O(NlogN)$

2) 의사코드 및 구현 코드

quick_sort(A[p..r]) { # A[p..r]을 오름차순 정렬한다.
    if (p < r) then {
        q <- partition(A, p, r);  # 분할
        quick_sort(A, p, q - 1);  # 왼쪽 부분 배열 정렬
        quick_sort(A, q + 1, r);  # 오른쪽 부분 배열 정렬
    }
}

partition(A[], p, r) {
    x <- A[r];    # 기준원소
    i <- p - 1;   # i는 x보다 작거나 작은 원소들의 끝지점
    for j <- p to r - 1  # j는 아직 정해지지 않은 원소들의 시작 지점
        if (A[j] ≤ x) then A[++i] <-> A[j]; # i값 증가 후 A[i] <-> A[j] 교환
    if (i + 1 != r) then A[i + 1] <-> A[r]; # i + 1과 r이 서로 다르면 A[i + 1]과 A[r]을 교환
    return i + 1;
}

위 그림은 각 영역의 첫번째 원소가 pivot
의사코드는 각 영역의 마지막 원소가 pivot

7. 계수 정렬 (Counting sort)

1) 개념

• 비비교 정렬 (비교를 하지 않는 정렬)
• 해당 원소가 몇번 나오는지를 기반으로 정렬
• stable하게 정렬하려면, 누적합을 인덱스로 사용
• 음의 값을 가진 원소가 있거나, 원소가 듬성듬성 있으면 비효율적
• $O(N + K)$

2) 의사코드 및 구현 코드

counting_sort(A[p..r]) { # A[p..r]을 오름차순 정렬한다.
	for i <- p to r
    C[A[i]]++;

    for i <- 2 to k # 누적 합
    C[i] += C[i-1]

    for i <- r to p{ # 들어갈 위치 지정
    B[C[A[i]]-1] = A[i]
    C[A[i]]--;
    }
}

#include <iostream>
#include <string>
#include <vector>
using namespace std;

string solution(string s)
{
    vector<int> count (26, 0);
    string answer(s.size(), '0');
    for (auto& c : s)
    {
        count[c-'a']++;
    }

    for (int i=1; i<count.size(); i++)
    {
        count[i] += count[i-1];
    }

    for (auto it = s.rbegin(); it != s.rend(); ++it)
    {
        int index = count[*it - 'a'] - 1;
        answer[index] = *it;
        count[*it - 'a'] --;
    }

    return answer;
}

int main()
{
  cout << solution("hello") << endl; // 출력값 : ehllo
  cout << solution("algorithm") << endl; // 출력값 : aghilmort

  return 0;
}

8. 위상 정렬 (Topological sort)

1) 개념

• 사이클이 없는 방향 그래프의(DAG) 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것'을 의미.
• 진입차수가 0인 노드들을 Queue에 넣음 (진입차수: 자신에게 들어오는 간선의 개수)
• Queue가 빌 때까지 아래를 반복
  • Queue에서 front를 뽑아옴
  • front에 인접한 노드들의 진입 차수를 낮춤
    • 진입 차수가 0이면 Queue에 삽입
• 위 과정에서 Pop한 순서가 위상 정렬의 결과
• $O(V+E)$

2) 의사코드 및 구현 코드

topological_sort(G):
    for 각 정점 v:
        in_degree[v] ← 0

    for 각 간선 (u → v):
        in_degree[v] ← in_degree[v] + 1

    Q ← 진입 차수가 0인 모든 정점을 큐에 삽입

    while Q가 비어있지 않다면:
        v ← Q에서 꺼냄
        v를 결과 리스트에 추가

        for v의 모든 인접 정점 w:
            in_degree[w] ← in_degree[w] - 1
            if in_degree[w] = 0:
                Q에 w를 추가

    if 결과 리스트에 모든 정점이 없다면:
        "사이클 존재"
    else:
        결과 리스트 출력

9. C++에서의 정렬

1) std::sort()

• intro_sort 사용 (heap, quick, insertion)
• $O(NlogN)$
• default (1) : template void sort (RandomAccessIterator first, RandomAccessIterator last);
  • 기본적인 정렬 [fisrt, last)까지 오름차순 정렬 (std::less와 동일 효과)
• custom (2) : template <class RandomAccessIterator, class Compare> void sort (RandomAccessIterator first, RandomAccessIterator last, Compare comp);
  • comp 매개 변수에 함수(람다 포함), Functor를 넣어서 원하는 순서로 정렬 할 수 있음
• 참고로 return 값이 false이면 swap하기 때문에 잘 생각해서 넣자
  • return a < b 면 오름차순 (a가 b의 앞에 올 수 있는지에 대한 true false)
  • return a > b 면 내림차순
• 우선순위 큐에서는 a, b중 어떤 것이 우선순위가 높은지
  • Compare(a, b) 가 true면 → a가 우선순위가 낮음.