재귀함수

• 재귀(recursion)는 함수가 자기 자신을 호출하는 것을 말한다.

  • 재귀를 중단시키는 기저 조건(base case),
  • 기저 조건으로 수렴하게 되는 재귀 조건(recursive case)으로 구성된다.

• 재귀호출을 사용하는 이유 : 문제에 따라 전체를 한 번에 해결하기보다 같은 유형의 하위 작업으로
  분할하여 작은 문제부터 해결하는 방법 분할 정복법이 효율적일 수 있기 때문.

• 재귀의 단점 : 함수 호출에 따른 오버헤드(overhead)가 있다는 것이다.
  재귀가 너무 깊어지면 그만큼 호출 스택의 공간을 더 많이 사용하게 되고,
  끝내는 스택 오버플로(stack overflow)가 발생할 수 있다.

• 오버헤드 : 어떤 처리를 하기 위해 들어가는 간접적인 처리 시간 · 메모리 등을 말한다.
  

• 스택 오버플로 : 스택이 가용할 수 있는 공간을 벗어나는 것을 말한다.

---

예시 문제

백준 10872번 : 팩토리얼

> 0보다 크거나 같은 정수 N이 주어진다. 이때, N!을 출력하는 프로그램을 작성하시오.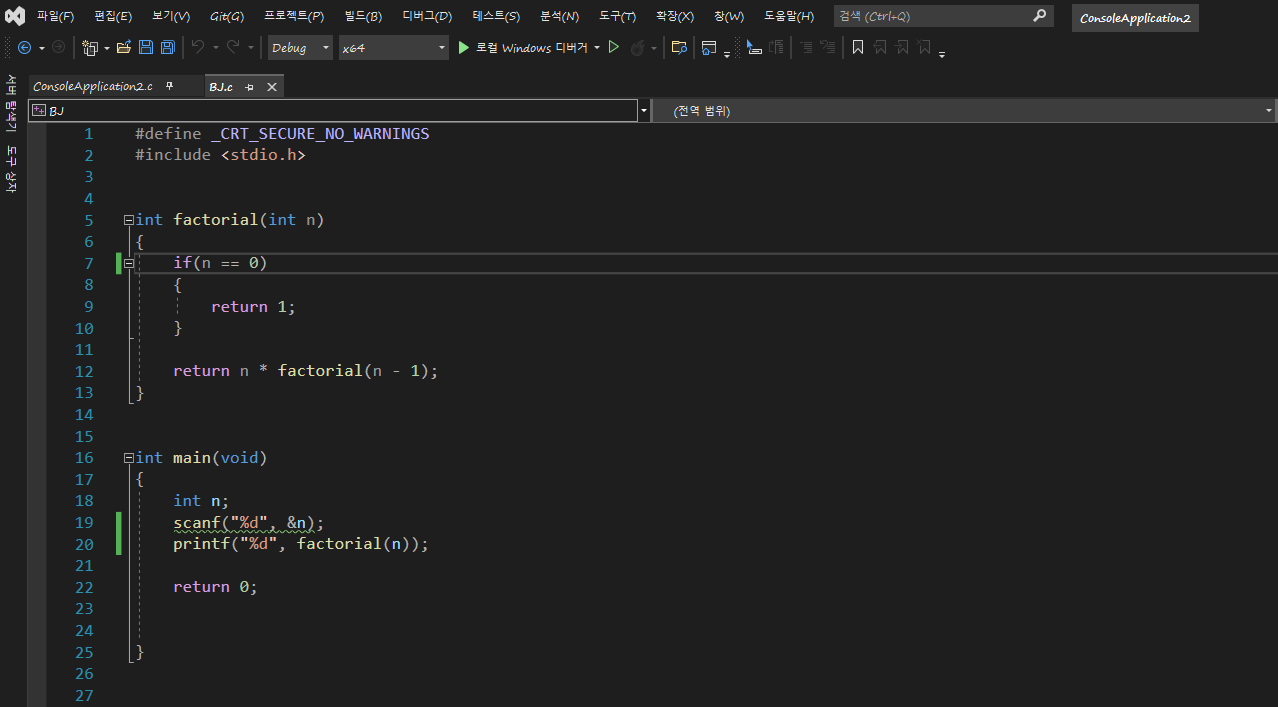

• 기본적인 재귀함수 문제로 정수 n이 0일 때의 기저 조건과
  기저 조건으로 수렴하게 되는 재귀 조건을
  팩토리얼을 구하는 점화식인 n (n -1) ... 1 을 재귀조건로 구성,
  main함수에서 입력과 출력으로 나타낸다.

• 예시와 같은 값이 나오는 것을 확인할 수 있다.

백준 17478번 : 재귀함수가 뭔가요

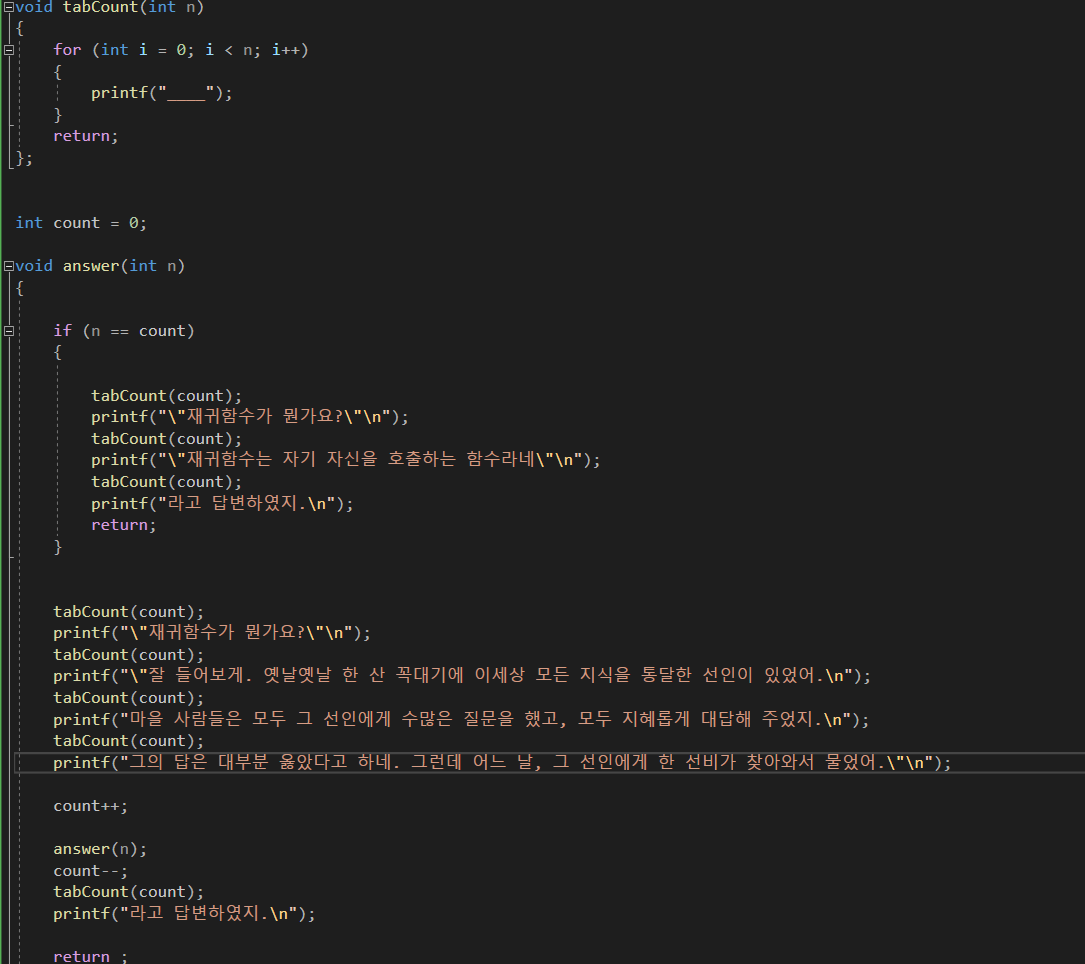
• 이 문제는 텍스트를 연속적으로 출력하면서, 한번 호출할 때마다 텍스트 앞에 언더바를 늘려가야하는 문제이다.
  

• 우선 언더바를 출력하기 위한 tabCount 함수를 만들어 놓고 답변이 나오는 answer함수를 구성하였다.
  

• main 함수에는 바뀌지 않는 텍스트와 answer함수를 호출시켰다.
  

• 우선 tabCount와 출력할 텍스트로 재귀조건을 구성한 뒤, 출력 횟수를 세는 count 변수를 가산하였고,
  

• 입력받은 정수 n을 재귀로 호출하였다. 이후 기저조건으로 n과 count가 같을 때 마지막 텍스트를 출력하면,

  

• 출력 값이 정상적으로 나오는 것을 확인할 수 있다.

백준 2447번 : 별 찍기 - 10

> 재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다.

크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이 하나씩 있는 패턴이다.

***
* *
***

N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다.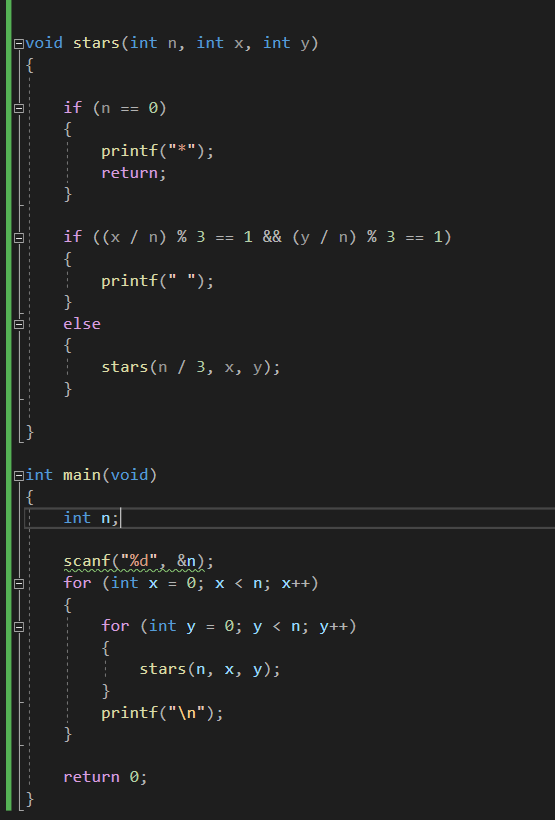 

• 이 문제는 프랙탈 형태의 별찍기로, 해답을 위하여 규칙을 찾아내야 한다.
  
• 우선 정수 n은 3의 거듭 제곱이고, (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다.
  이를 식으로 나타내면

  // (x / 3^0) % 3 == 1 && (y / 3^0) % 3 == 1 or
  // (x / 3^1) % 3 == 1 && (y / 3^1) % 3 == 1 or
  // (x / 3^2) % 3 == 1 && (y / 3^2) % 3 == 1 or
  // ...
  // (x / 3^(K - 1)) % 3 == 1 && (y / 3^(K - 1)) % 3 == 1

• 이와 같이 나타낼 수 있다.
  
• 따라서, n이 0이라면 *을 출력하고, (x / n) % 3 == 1 거나 (y / n) % 3 == 1 이라면 공백을 출력한다.
  
• n이 3의 거듭제곱이 아니라면, n / 3으로 재귀 조건으로 회귀할 수 있도록 해준다.
  
• 이후 main함수에서 x축과 y축을 모두 검사하고 별과 공백을 조건에 맞춰 찍어 준다면
  
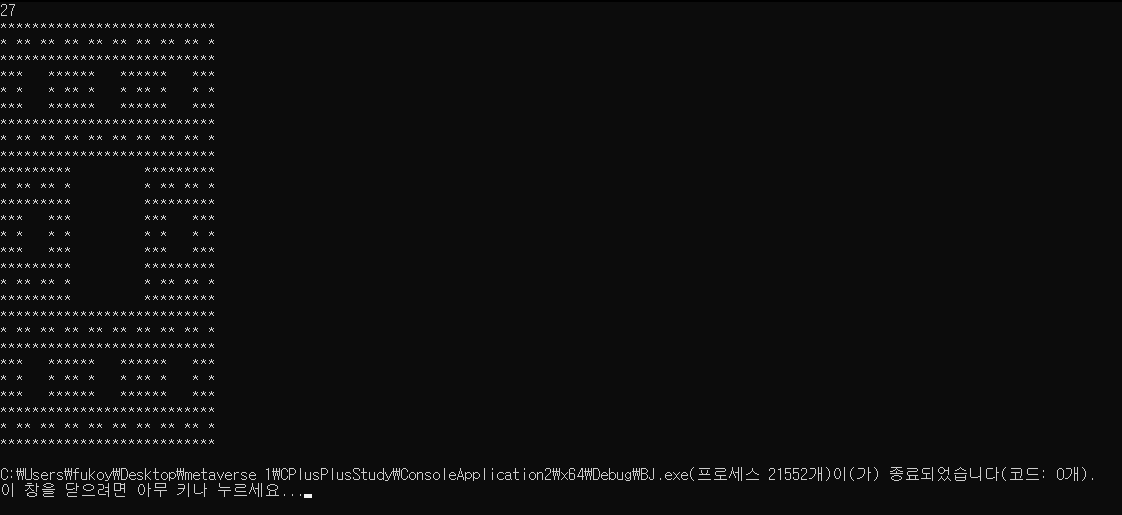
• 위와 같이 값이 잘 나온 것을 확인할 수 있다.

---

자료구조

• 자료구조 : 선형 구조(linear structure), 비선형 구조(non-linear structure).

  • 선형 구조 : 리스트, 스택, 큐.
  • 비선형 구조 : 그래프, 트리.

• 대부분의 자료구조는 네 가지 기본 방법을 사용하며 이를 연산이라고 한다.

  • 읽기 : 자료구조 내 특정 위치를 찾아보는 것이다.
  • 검색 : 자료구조 내 특정 값을 찾는 것이다.
  • 삽입 : 자료구조에 새로운 값을 추가하는 것이다.
  • 삭제 : 자료구조 내 특정 값을 삭제하는 것이다.

• 자료구조를 구현하는 방법 : 순차 자료구조(contiguous data structure), 연결 자료구조(linked data structure).

• 순차 자료구조 : 구현할 자료들을 논리적인 순서대로 메모리에 연속하여 저장하는 구현 방식. 배열 이용.

• 연결 자료구조 : 노드라는 여러 개의 메모리 청크에 데이터를 저장하며, 이를 연결하여 구현하는 방식. 포인터 이용.

• 알고리즘의 분석
  알고리즘이란 문제를 해결하기 위한 절차를 말한다.
  문제를 해결하는 방법에는 여러가지가 존재할 수 있으며, 우리는 이 중 최선을 선택해야 한다.
  자원을 적게 사용할 수록 효율적인 알고리즘.

• 시간 복잡도
  알고리즘의 분석에 있어 가장 중요한 부분은 실행 시간이다.
  시간 복잡도(time complexity)는 알고리즘을 수행하는 데 필요한 연산이 몇 번 실행되는지를 숫자로 표기한다.
  이 연산의 개수는 상수가 아니라 입력한 데이터의 개수를 나타내는 n에 따라 변하게 된다.

• 실행 시간의 성장률 : 입력값이 작을 때는 그 차이가 크지 않았지만, 입력값이 점점 커질 수록 엄청나게 차이가 벌어진다는 것.
  따라서 효율적인 알고리즘을 구상해야함.

• Big-O 표기법

  • 상수 계수와 중요하지 않은 항목을 제거한 점근적 표기법(asymptotic notation)을 사용한다.

  • Big-O 표기법은 점근적 상한선을 제공한다.

    앞선 시간 복잡도 함수를 Big-O 표기법으로 나타내면 각각 O(1), O(n), O(n2)으로 나타낼 수 있다. 

  • Big-O 표기법은 오른쪽으로 갈 수록 상한선이 높아진다.
    왼쪽에 위치한 시간 복잡도일수록 해당 알고리즘은 빠르다고 할 수 있다.

O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)

• 유의할 점은 한 알고리즘이 다른 알고리즘보다 실제로 빠르다고 하더라도 같은 방식으로 표현이 될 수도 있다는 것이다.
  따라서 같은 카테고리라면 어떤 알고리즘이 더 빠른지 면밀한 분석이 필요할 때가 있다.

• 공간 복잡도 : 알고리즘의 성능을 측정할 때는 실행 시간만 따지지 않는다.
  컴퓨터 내의 자원 공간을 얼마나 사용하는지도 따져봐야 한다.
  공간 복잡도(space complexity)는 알고리즘을 수행하는 데 필요한 자원 공간의 양을 말한다.

• 시간 복잡도 vs 공간 복잡도
  여태까지 배운 내용을 토대로 정리하자면 효율적인 알고리즘은 실행 시간이 적게 걸리며, 자원을 적게 소모하는 것이라고 할 수 있다. 하지만 시간과 공간은 반비례적인 경향이 있어 보통 알고리즘의 척도는 시간 복잡도를 위주로 판단한다. 즉, 시간 복잡도를 위해 공간 복잡도를 희생하는 경우가 많다.

• 리스트
  리스트(list)는 순서를 갖고 있는 자료구조다. 순차 자료구조엔 선형 리스트가 있고, 연결 자료구조엔 단일 연결 리스트, 원형 연결 리스트, 이중 연결 리스트가 있다.

• 선형 리스트
  선형 리스트(linear list)는 순서 리스트(ordered list)라고도 하며 STL 상에서는 std::array, std::vector로 구현되어 있다.
  임의 접근이 가능하다는 특징을 가지고 있다.

  • 읽기 : 선형 리스트는 임의 접근이 가능하기 때문에 O(1)의 시간이 걸린다.
  • 검색 : 하나하나 원소를 비교해가야 하므로 O(n)의 시간이 걸린다. 정렬되어 있다면 이진 검색을 사용할 수 있으며 이 경우 O(logn)이다.
  • 삽입 : 원소를 어디에 삽입하냐에 따라 시간이 달라진다. 맨 끝에 데이터를 추가할 경우 O(1)이지만, 처음이나 중간이라면 모든 데이터를 이동해야 하기에 O(n)이 걸린다.
  • 삭제 : 삽입과 마찬가지로 원소를 어디에서 삭제하냐에 따라 시간이 달라진다. 맨 끝의 데이터를 삭제할 경우 O(1)이지만, 처음이나 중간이라면 모든 데이터를 이동해야 하기에 O(n)이 걸린다.

• 스택
  스택(stack)은 리스트의 일종으로 연산이 한 쪽 끝에서만 이뤄지는 자료구조다.
  가장 나중에 들어간 것이 처음에 나옴 (LIFO (Last-In First-Out) 구조).
  스택의 끝을 위(top), 스택의 시작을 밑(bottom)이라 한다. 괄호가 올바른지 검사 / 후위 표기식 / DFS 등에 사용될 수 있다.
  STL에서는 std::stack으로 구현되어 있다.

• 큐
  큐(queue)도 리스트의 일종으로 스택과 다르게 가장 처음에 들어간 데이터가 처음에 나옴 (FIFO (First-In First-Out) 구조).
  삽입이 일어나는 쪽을 뒤(rear), 삭제가 일어나는 쪽을 앞(front)라고 한다.
  프린트 큐 / CPU 스케줄링 / 데이터 버퍼 / BFS 등에 사용된다.
  STL에서는 std::queue, std::deque로 구현되어 있다.

• 그래프
  선형 자료구조로는 표현할 수 없는 문제가 있다.
  회사의 조직도와 같은 계층을 표현한다던가 인스타그램 친구 관계도를 표현하는 것처럼 말이다.
  이번 챕터부터는 이런 비선형적 문제를 다룰 수 있는 자료구조에 대해서 배우게 된다.

  • 종류
    • 그래프의 종류에는 간선이 방향성을 가지는 지에 따라 방향 그래프(directed graph),
    • 무방향 그래프(undirected graph)로 구분.
    • 간선이 단순 연결 이상의 정보를 가지는 가중치 그래프(weighted graph)도 있다.

• 순회
  한 정점에서 시작해 그래프에 있는 모든 정점을 한 번씩 방문하는 것을 그래프 순회(graph traversal) 또는 탐색(search)이라 한다. 이러한 방법에는 깊이 우선 탐색(depth first search)과 너비 우선 탐색(breadth first search)이 있다.
  • 깊이 우선 탐색은 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다 더 이상 갈 곳이 없으면 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와 다른 방향의 간선으로 탐색을 계속하는 방법으로 스택을 사용한다.

    • 너비 우선 탐색은 시작 정점에 인접한 정점을 모두 차례로 방문하고 나서 방문했던 정점을 시작으로 다시 인접한 정점을 차례로 방문하는 방식으로 큐를 사용한다.

• 트리
  트리(tree)는 그래프의 일종으로 계층형 자료구조(hierarchical data structure)다.
  트리는 데이터가 저장된 노드(node)와 노드 간 관계를 표현하는 간선(edge)으로 구성된다.
  STL에서는 std::set / std::map / std::multiset / std::multimap 으로 구현이 되어 있다.

  • 조상(ancestor) 노드 : 한 노드에서 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드
  • 자손(descendant) 노드 : 조상 노드의 반대
  • 차수(degree) : 한 노드가 가지는 서브 트리의 수. 노드의 차수 중 최댓값을 트리의 차수라 한다.
  • 내부(internal) 노드 : 단말 노드를 제외한 나머지 노드
  • 포레스트(forest) : 트리의 집합

• 순회
  트리에 대한 순회는 전위 순회(pre-order traversal) / 중위 순회(in-order traversal) / 후위 순회(post-order traversal) / 레벨 순회(level-order traversal)가 있다.

• 힙
  힙(heap)은 완전 이진 트리에 있는 노드 중에서 키값이 가장 큰 노드나 키값이 가장 작은 노드를 찾기 위해 만든 자료구조다.

  • 최대 힙(max heap) : 키값이 가장 큰 노드를 찾기 위한 힙.
  • 최소 힙(min heap) : 가장 작은 노드를 찾기 위한 힙. 우선순위 큐(priority queue)라고도 한다.
  • STL에서는 std::priority_queue로 구현이 되어 있다.

• 연산

  • 검색 및 읽기 : 최대 / 최소 원소에 대해서만 가능하며 O(1)이다.
  • 삽입 : 완전 이진 트리이기 때문에 O(logN)이다.
  • 삭제 : 최대 / 최소 원소에 대해서만 가능하며 O(logN)이다.

• 힙의 불변성

  • 힙은 최대 / 최소 원소에 즉각적으로 접근이 가능해야 한다.
  • 따라서 최대 / 최소 원소가 항상 고정된 위치에 있어야 한다.
  • 그래서 최대 / 최소 원소는 항상 트리의 루트에 존재한다.
  • 또, 부모 노드가 두 자식 노드보다 항상 크거나 작아야 한다.

• 해싱(hashing) : 입력의 크기에 상관 없이 일정 크기의 값으로 변환하는 것. 문자를 가져와 숫자로 변환하는 과정.
  이에 사용되는 함수를 해시 함수(hash function)라 한다.

  • 균일성 : 충돌이 적은 것을 의미한다.
  • 충돌(collision) : 서로 다른 값이 같은 해시 값을 생성한 것
  • 효율성 : 계산하기 쉬워야 한다.
  • 결정적 : 같은 입력에는 같은 값을 내놓아야 한다. Ex) 디지털 서명, 공인 인증서 등등등등

• 해시 테이블(hash table) : 해싱을 활용해 데이터를 저장하는 검색을 위한 자료구조.