Today's BaekJoon [백준 1929번 문제 : 소수 구하기] & 에라토스테네스의 체

백준 1929번 문제 : 소수 구하기

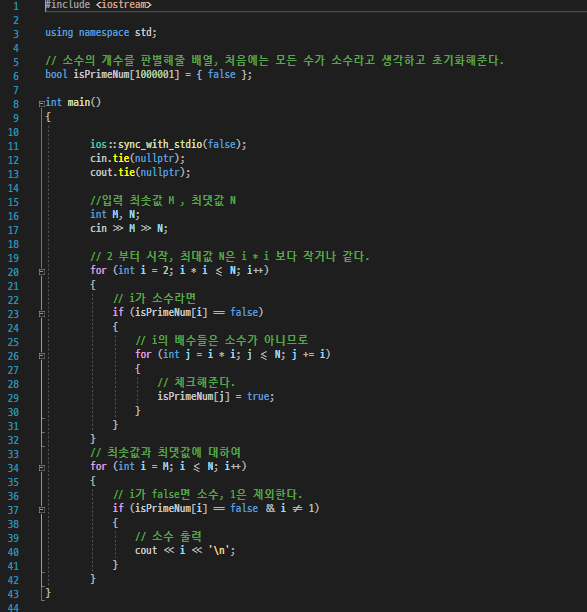
소수 문제 중 쉬운 편의 문제였으나, 직접 소수를 구하려면 범위가 넓어서 시간 초과가 발생했다.
때문에 에라토스테네스의 체라는 것을 사용해야만 했다.
고대 그리스의 학자였던 에라토스테네스는 소수를 찾아내는 방법을 고안해냈다.
자연수들 중, 소수가 아닌 합성수를 제거하는 방식이다.
에라스토테네스의 체 (Wikipedia)
워낙에 자주 쓰이고, 어렵지 않은 방법이어서 익히는 것은 어렵지 않았다.
간단히 코드로 설명하자면,

// 에라토스테네스의 체 알고리즘
// 범위를 매개변수로 받는다.
void Eratos(int numRange)
{ 
	// 1은 소수가 아니므로, 매개변수가 1이면 소수가 아니다.
	if (num <= 1) 
		return;

	// 소수를 판별해줄 bool 배열. 
	bool* isPrimeNum = new bool[num + 1];
 
	// 모든 범위의 값에 대해여 true 값을 준다.
    // 즉, 처음에는 모든 수를 소수로 만들어준다.
	for (int i = 2; i <= num; i++)
		isPrimeNum[i] = true;

	
	// 가장 작은 소수인 2부터 시작하며, i * i 는 범위보다 작거나 같다.
	for (int i = 2; i * i <= num; i++)
	{
		// 만약 i가 소수라면
		if (isPrimeNum[i])
		{
			// i의 배수들은 소수가 아니므로
			for (int j = i * i; j <= num; j += i)
			{
				// 제외해준다.
				isPrimeNum[j] = false;
			}
		}
	}
}

에라토스테네스의 체를 활용하여 소수문제를 아주 쉽게 풀 수 있었다.