
문제 설명
올바른 괄호 찾기 문제의 응용버전으로 주어진 괄호로 이루어진 문자열중, 올바르게 연결된 괄호의 최대길이를 반환하는 문제입니다.
- 괄호는 소괄호로만 이루어져 있습니다.
| 💬 input | ✅ output |
|---|---|
(() | 2 |
| )()()) | 4 |
| ()(() | (🔥주의 4가 아니라 )2 |
💡 접근 및 1차 풀이
(1) 스택을 사용해서 올바른 괄호인지를 판별하고
(2) 배열에 올바른 괄호인지를 저장하고 (올바른 괄호이면 1, 올바르지 않은 괄호이면 0)
(3) 배열을 훝으며 가장 긴 1의 길이를 리턴
괄호 판별문제는 전형적인 Stack을 사용한 문제기 때문에 큰 고민없이 1차 답안을 제출하였습니다.
/**
* @param {string} : 괄호로 이루어진 문자열
* @return {number} : 가장 긴 연속된 올바른 괄호의 길이
*
* example
* ()(() : 4가 아니라 2
* note : [ 1, 1, 0, 1, 1 ]
*/
var longestValidParentheses = function(s) {
// (1) 올바른 괄호인지 판단하여 Note를 작성
const note = new Array(s.length); // 올바른 괄호이면1, 올바르지 않은 괄호이면 0
const stack = [];
s.split('').forEach((paranth, index) => {
if(paranth === ')' && stack[stack.length-1]&&stack[stack.length-1][0] === '('){
const [popedParanth, popedIndex]= stack.pop();
note[index] = 1;
note[popedIndex] = 1;
}else{
stack.push([paranth,index])
}
})
while(stack.length >0){
const [last, lastIndex] = stack.pop();
note[lastIndex] = 0 ;
}
// (2) note에서 연속적으로 나타나틑 1의 가장 긴 길이를 리턴
// 🍀 연속적인 올바른 수열의 길이?
// 1 -> 1 인경우 현재 길이에 +1
// 0 -> 1 인경우 현재길이를 초기화 하고 1
let max = 0 ; // 최종적으로 반환해야 하는 값
let curr = 0 ;
note.forEach((num, index) => {
if(index == 0 ){
if(num === 1) {curr += 1;
max = Math.max(max, curr);}
return ;
}
if(num === 1){
const lastNum = note[index-1];
if(lastNum === 1){
curr += 1;
max = Math.max(max, curr);
return ;
}else if(lastNum === 0 ){
curr= 1;
max = Math.max(max, curr);
}
}
})
return max;
};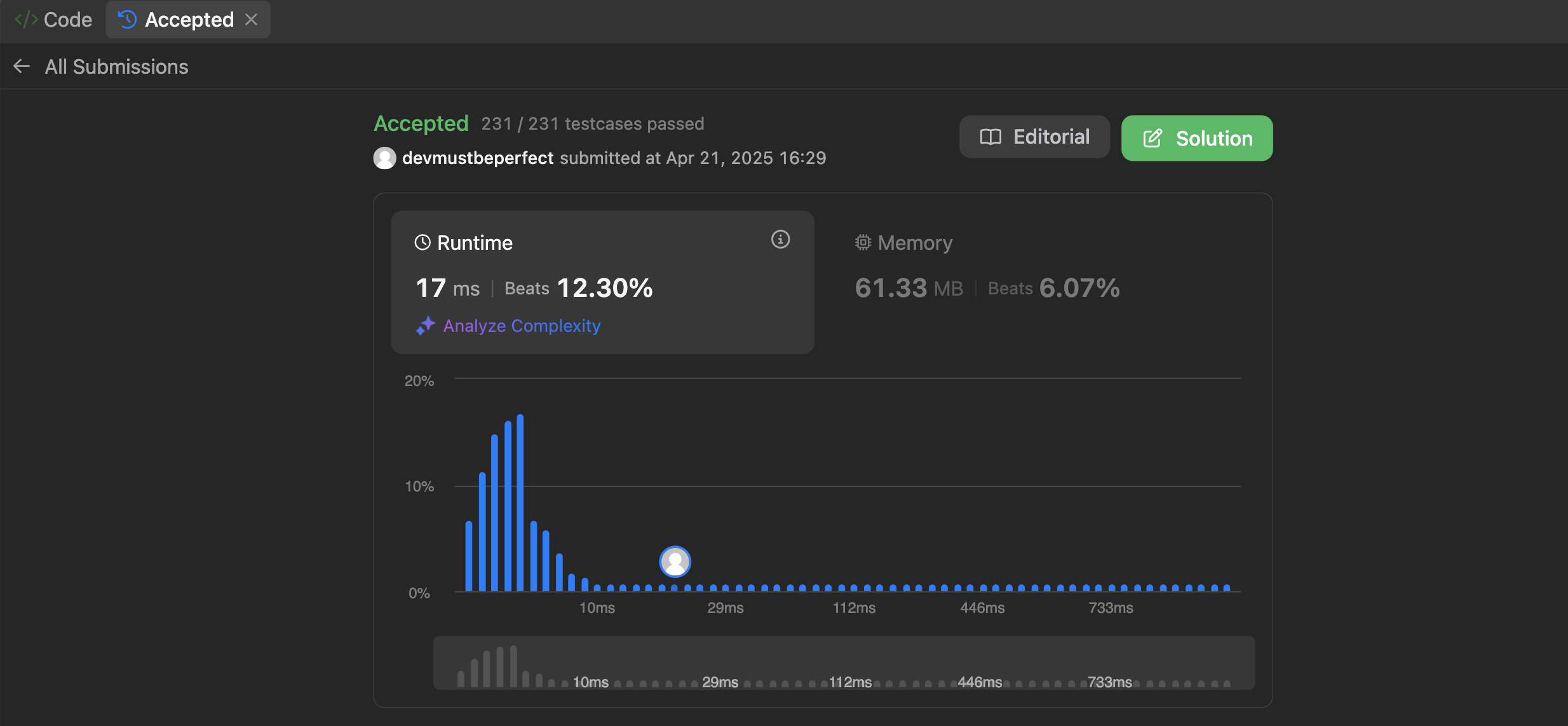
문제는 맞췄지만 처참한 효율성 점수에 충격을 받고 다시 고민을 해보았습니다.
🔥 2차 풀이
이전에 풀이 방식은 크게 두가지 파트로 나누어져 있습니다.
(1) 올바른 괄호인지 판별하기
(2) note배열에서 가장 긴 연속적인 1의 길이 찾기
두번째 파트인 연속적인 1의 길이를 좀 더 효율적으로 찾는 방법을 없을까 고민해봅시다.
이전에는 배열을 순회하며 연속적으로 1이 나오는 최대길이를 업데이트 하는 방식을 사용했기 때문에 최대 O(N)의 시간복잡도를 가집니다.
그런데 note배열의 경우 아래와 같은 특징을 가집니다.
[0,1,1,1,0,1,1,0,0,0,1,1]처럼 0과 1로만 이루어져 있다.- 0인 부분은 굳이 훝지 않아도 된다.
때문에 note 배열을 문자열로 합친뒤, 다시 0을 기준으로 split 해준다면 좀더 빠르게 1로 만 이루어진 문자열을 구할 수 있을 것이라 생각했습니다.
위의 코드에서 (2) 번 부분을 아래처럼 바꿀 수 있겠습니다.
// note에서 연속적으로 나타나틑 1의 가장 긴 길이를 리턴
// 0을 기준으로 자르고 남은 1로 이루어진 문자열 배열중 가장 긴 길이를 ㄹ반환.
return note.join('').split('0').reduce((max, curr) => curr.length > max ? curr.length : max, 0)
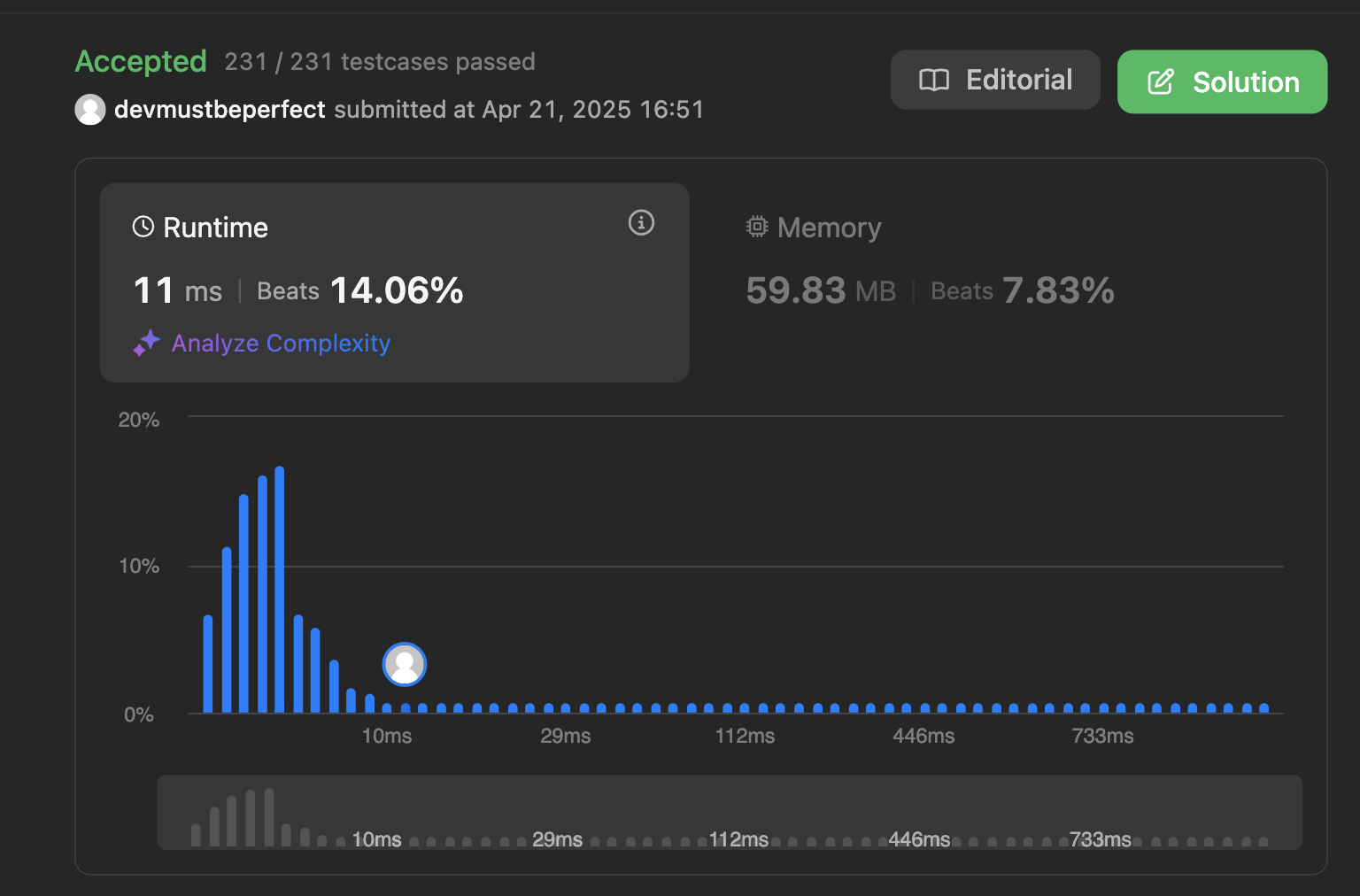
이전에 비해 17ms에서 11ms로 조금 나아졌지만 더 나은 방법이 있을것 같습니다.
현재처럼 단계를 1,2 단계로 나누지 말고 단일루프내에서 길이를 구해보겠습니다.
🚀 3차 풀이
리팩토링 방향
- 추가 메모리인 note 배열을 제거한다.
- stack에 괄호가 아닌, index를 담는다.
- 문자열을 여러번 순회하지 않고 한번의 순회로 최대 길이를 계산한다.
이전 코드와 달라지점은 pop을 하는 조건인데, 이전 코드에서는 괄호가 올바르게 짝을 이룰경우 괄호쌍을 pop 하였습니다.. 리팩토링된 코드에서는 올바르지 않은 쌍이라도 닫는 괄호일 경우 Pop을 일으키도록 설계하였습니다.
여기서 중요한 점은 무턱대고 pop을 하는것이 아닌 짝을 맞추는 도중 실패했을 때 새로운 유효구간을 정하는 용도로 pop 후 현재 index를 push 한다는 것입니다.
즉, stack이 비어있다면 더이상 유효하지 않은 괄호문자열이란 뜻이고(이전 코드에서 note[i] === 0 이 되버리는 부분), 새로운 인덱스를 기준점으로 초기화해야하므로 pop -> push(i) 가 일어나는 것입니다.
📌 stack이 비는 상황
1️⃣. 문자열이 ')'로 시작할 때
예: ")(()())"
첫 글자가 닫는 괄호이므로, 스택은 [-1]에서 pop이 되고 비어지게됩니다..
2️⃣. 괄호의 짝이 맞지 않을 때
예: (()))(())
5번째에서 닫는 괄호가 추가적으로 등장합니다. 짝이 될 여는괄호(()는 이미 다 pop 되었으므로, 이때 한번더 pop하면 -1이 나가면서 스택이 비어지게 됩니다.
var longestValidParentheses = function(s) {
let max = 0 ;
let stack = [-1]
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
stack.push(i);
} else {
stack.pop();
if (stack.length === 0) {
// 올바른 시작 기준점이 사라졌으면 현재 인덱스를 기준점으로 새로 세움
stack.push(i);
} else {
// 현재 인덱스와 스택 마지막 값의 차이가 유효한 길이
max = Math.max(max, i - stack[stack.length - 1]);
}
}
}
return max;
};
| 시도 | 최종 |
|---|---|
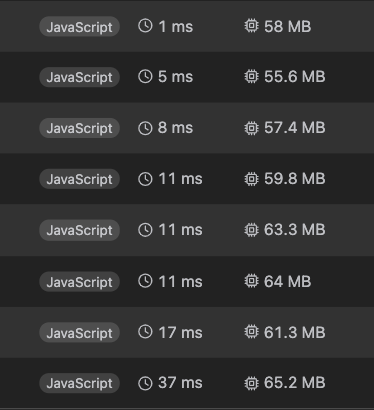 | 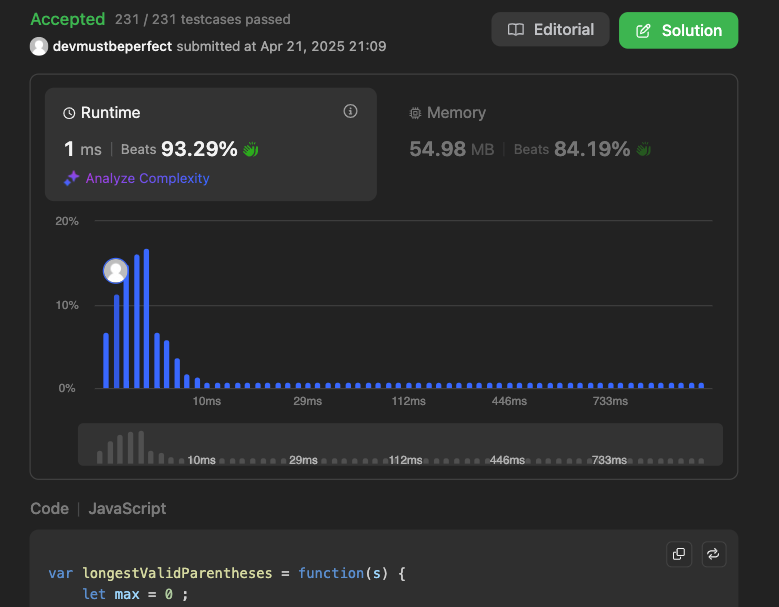 |
😭 최종적으로 1ms 이내로 수행시간이 줄어들게 되었습니다.
이전에 스터디원들과 함께 한문제를 어떻게 풀지 여러 각도에서 고민해본적이 있었는데 이를 개인 공부에도 적용시켜보면서 풀어보았습니다.
하루에 여러문제를 풀 수도 있겠지만, 수행시간과 메모리 관점에서 어떻게하면 적은 메모리로 빨리 풀 수 있을지 생각하다보니
자료구조와 알고리즘의 개념을 체화하는데 더 도움이 되었던것 같습니다.
앞으로도 이 방법을 종종 사용해봐야겠다는 생각이 듭니다...
