주저리주저리~ 백준 컬러 #428BCA font Song Myung 60
원본
문제 설명
+---+
| D |
+---+---+---+---+
| E | A | B | F |
+---+---+---+---+
| C |
+---+ A, B, C, D, E, F가 적힌 주사위 전개도를 접는다.
동일한 주사위 N^3개를 회전/쌓기 하여 N×N×N 크기의 정육면체를 만드려 한다.
N×N×N 정육면체의 5면(바닥면 제외) 에 쓰인 수의 합의 최솟값을 출력하라.
-
입력
N
1 2 3 4 5 6 (=> A B C D E F) -
출력
합의 최솟값
아이디어
생각해야 하는 것은 보이는 5면에 보일 숫자들을 최대한 작게 만드는 것
작은 숫자들이 최대한 겉에 놓아야 하며, 보여지는 면의 경우는 2가지로 나눌 수 있다.
1. 윗 면
개수: 1개
주사위의 경우의 수: 3개
1) 주사위 6면 중 한 면만 보인다.
2) 주사위 6면 중 한 변이 맞닿은 2면만 보인다.
3) 주사위 6면 중 한 모서리를 둘러싼 3면만 보인다.
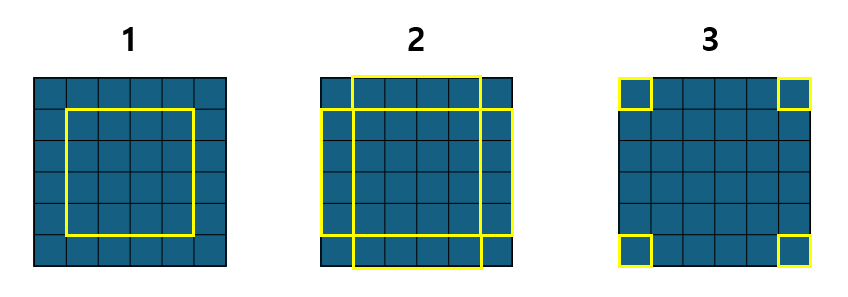
2. 옆 면
개수: 4개
주사위 경우의 수: 2개
6번의 경우에는 2, 3번과 중복이기 때문에(윗면이다) 고려하지 않아도 된다.
4) 주사위 6면 중 한 면만 보인다.
5) 주사위 6면 중 한 변이 맞닿은 2면만 보인다.
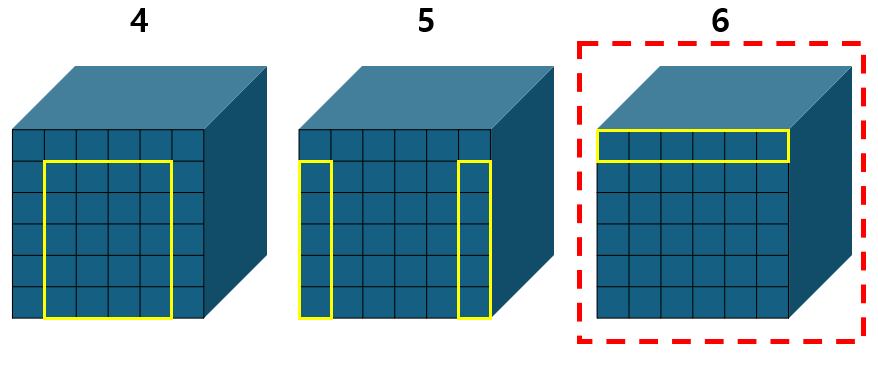
이렇게 총 5개의 경우가 있다.
1. 한 면만 보이는 주사위의 개수 => 가장 작은 수를 배치해야 한다.
1)의 경우: (N-2)개×(N-2)개
4)의 경우: (N-2)개×(N-1)개×4면
2. 두 면만 보이는 주사위의 개수 => 두 면의 합이 가장 작은 면
2)의 경우: (N-2)개×4줄
5)의 경우: (N-1)개×4줄
3. 세 면만 보이는 주사위의 개수 => 세 면의 합이 가장 작은 면
3)의 경우: 4개
각 경우는 모두 독립적이므로 각각 구하여 총 합을 더하면 된다.
코드
import sys
input = sys.stdin.readline
ans = 0
N = int(input())
dice = list(map(int, input().split()))
if N == 1:
dice.sort()
for i in range(5):
ans += dice[i]
else:
# 주사위 한 면의 최솟값
one_side = min(dice)
# 주사위 두 면의 최솟값
# AB, AC, AD, AE, BC, BD, BF, CE, CF, DE, DF, EF : 12개
# 0-5, 1-4, 2-3 제외하기 => i+j=5 가 아닐 때
two_side = sum(dice)
for i in range(6):
for j in range(i+1, 6):
if i+j != 5 and i != j:
two_side = min(two_side, dice[i]+dice[j])
# 주사위 세 면의 최솟값
# ABC, ABD, ACE, ADE, BCF, BDF, CEF, DEF
three_side = min(dice[0] + dice[1] + dice[2],
dice[0] + dice[1] + dice[3],
dice[0] + dice[2] + dice[4],
dice[0] + dice[3] + dice[4],
dice[1] + dice[2] + dice[5],
dice[1] + dice[3] + dice[5],
dice[2] + dice[4] + dice[5],
dice[3] + dice[4] + dice[5])
ans += one_side * ((N-2) ** 2 + (N-2) * (N-1) * 4)
ans += two_side * ((N-2) * 4 + (N-1) * 4)
ans += three_side * 4
print(ans)다른 사람의 코드 중 더 나았던 점
아래처럼 푼 사람이 있었는데, 이 사람은
A와 F 중, B와 E 중, C와 D 중 작은 값을 취한다.
이 값들 중 가장 작은 값이 1면
가장 작은 값과 두 번째로 작은 값을 더한 게 2면
모두 더한 게 3면
이런식으로 간단하게 구할 수 있었다.
원리는 간단한게,
1면은 자연스럽게 이해할 수 있고
2면과 3면이 어떻게 해서 저렇게 구할 수 있었냐 하면
주사위의 한 면은 "반대쪽 면을 제외한 다른 면과 변이 맞닿아 있다"라는 사실에 근거하여 이해할 수 있다.
+----+
| ♡ |
+----+----+----+----+
| △ | ★ | △ | ★ |
+----+----+----+----+
| ♡ |
+----+ 이렇게 보면, 같은 도형끼리 비교해서 최소값을 찾은 건데
두 ♡는 모두 어떤 ★, △과도 닿아 있다. ★, △ 입장에서 봤을 때도 마찬가지이다.
아무 {♡, ★} {♡, △}, {★, △} 쌍을 꺼내도 맞닿아 있다.
어느 {♡, ★, △} 쌍을 꺼내도 맞닿아 있음을 알 수 있다!!!
import sys
if __name__ == '__main__':
N = int(input())
arr = list(map(int, sys.stdin.readline().split()))
ans = 0
min_lists = []
if N == 1:
arr.sort()
for i in range(5):
ans += arr[i]
else:
min_lists.append(min(arr[0], arr[5]))
min_lists.append(min(arr[1], arr[4]))
min_lists.append(min(arr[2], arr[3]))
min_lists.sort()
# 1, 2, 3 면의 주사위 최소값
min1 = min_lists[0]
min2 = min_lists[0] + min_lists[1]
min3 = sum(min_lists)
# 1, 2, 3 면의 주사위 개수
n1 = 4 * (N - 2) * (N - 1) + (N - 2) ** 2
n2 = 4 * (N - 1) + 4 * (N - 2)
n3 = 4
ans += min1 * n1
ans += min2 * n2
ans += min3 * n3
print(ans)

너무 좋은 글인듯... 이미지까지 보니까 이해가 잘 되네요!! 저런 방법이..