트리 소개
TREES는 고전적인 데이터 구조를 뜻한다.
트리는 연결 리스트보다는 약간 더 상위 단계이고, 더 복잡한데 좀 더 흥미로워!
트리란?
- 트리는 연결리스트처럼 노드로 이루어진 데이터 구조다.
- 그렇지만. 노드들 사이에 부모-자식 관계가 있다.
- 이런식으로 가지가 있는 구조가 나오게 돼서 TREE다.
- 가장 최상위 노드 : root
- 하나의 노드가 여러 다른 자식 노드를 가리킬 수 있고, 아예 안가리킬 수도 있음
- 노드에 숫자나 스트링, 그 외 배열이나 아무거나 다 저장할 수 있다
- 리스트: linear , 트리: nonlinar(선형구조)
트리 규칙
- 노드는 자식 노드만 가리킬 수 있다. (자기와 같은 급 노드는 못가리킴)
즉, 부모, 형제 노드를 가리키면 안된다. - 트리에서는 모든 노드가 루트에서 멀어지는 방식으로 연결된다.
- 출발점, 즉 루트가 하나여야 한다.
트리용어
- Root : the top node in a tree
- Child : a node directly connected to another node when moving away from the root
- Parent : the convers notion of a child
- Siblings : a group of nodes with the same parent.
- Leaf : a node with no children
- Edge : the connection between one node and another
트리 사용
- HTML DOM
- Network Routing
- Abstract Syntax Tree
- Artificial Intelligence (인공지능)
- Folders in Operating Systems
- Computer File Systems (폴더-파일)
- JSON (만약 자바스크립트 객체 표기법인 JSOM으로 작업을 해봤다면 AJAX 호출 같은 것을 하게 되고, 그러면 API로부터 데이터가 온다. 그러면 스트링에서 온 응답을 입력하는 것이다. 트리를 순회하거나 트리같은 구조를 만드는 코드가 있다.)
이진 트리 소개
트리라는 데이터 구조는 많은 종류가 있다.
우리는 이진 트리를 대부분 배울 것이다.
- Trees
- Binary Trees : 다시 특정한 형태의 트리인것
- Binary Search Trees : 탐색에 강점을 보인다. 정렬된 데이터를 특정한 방식으로 저장한다.
이진트리
- 각 노드가 최대 두개의 자식을 가져야 한다는 조건이 있다. (자식이 0,1,2개)
- 순회가 쉽다는 장점이 있다.
- 트리의 한 종류다.
이진 탐색 트리 (BST)
- 노드당 최대 두개의 자식을 가진다.
- 특별한 방식으로 정렬이 되어있다.(데이터가 순서에 따라 정렬되어있다.)
- 데이터를 비교해서 정렬 가능하게 저장한다. (일반적으로 숫자를 다루긴함)
- 부모 노드의 왼쪽에 있는 모든 노드는 언제나 부모보다 작고, 부모 노드보다 오른쪽에 있는 모든 노드는 언제나 부모보다 크다.
- 이진트리의 특별한 종류다.
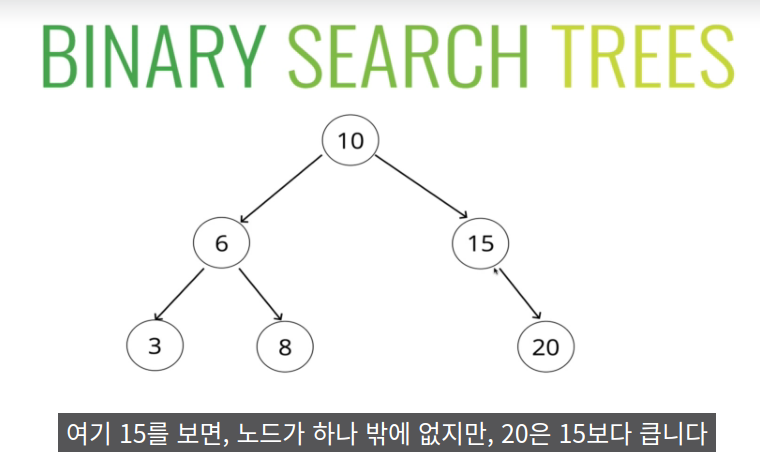
이진 검색 트리 찾기
왜 이것들이 사용되는가?
=> 무언가를 찾아보는 것을 아주 빠르고 쉽게 만들어준다.
=> 무언가를 추가하는 것과 노드의 자리를 찾는 것도 쉽게 해준다.
트리 클래스
기본 토대가 되는 두개의 클래스를 만들 것이다~~
class Node{
constructor(value){
this.value = value; // 각 노드는 값을 가진다.
this.left = null; // left 값과
this.right = null; // right 값
}
}
class BinarySearchTree{
constructor(){
this.root = null; // 딱 하나의 중요한 프로퍼티를 가진다. 루트!
}
}
let tree = new BinarySearchTree()
tree.root = new Node(10);
tree.root.right = new Node(15);
tree.root.left = new Node(7);
tree.root.left.right = new Node(9);insert 메소드 : 비교를 통해서 어떤 요소가 어디로 가야하는지 알려준다.
이진 검색 트리: insert 메소드
트리에 무언가를 삽입하는 방법을 추가하겠어!
이진 검색 트리: insert 메소드 솔루션
이진 검색 트리: Find 메소드
이진 검색 트리: Find 메소드 솔루션
(find, contains 함수 거의 비슷함)
class Node{
constructor(value){
this.value = value; // 각 노드는 값을 가진다.
this.left = null; // left 값과
this.right = null; // right 값
}
}
class BinarySearchTree{
constructor(){
this.root = null; // 딱 하나의 중요한 프로퍼티를 가진다. 루트!
}
insert(value){
let newNode = new Node(value);
if(this.root === null){
this.root = newNode;
return this;
}else{
let current = this.root;
while(true){
if(value < current.value){
if(current.left === null){
current.left = newNode;
return this;
}
current = current.right;
}
}
}
// 값, 노드를 출력하는 find
find(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(!found && current){
if(value < current.value){
current = current.left;
}else if(value > current.value){
current = current.right;
}else{
found = true;
}
}
if(!found) return undefined; // 값에 이 트리에 없다면
return current;
}
// 참과 거짓을 출력하는 contains고
contains(value){
if(this.root === null) return false;
let current = this.root,
found = false;
while(!found && current){
if(value < current.value){
current = current.left;
}else if(value > current.value){
current = current.right;
}else{
return true;
}
}
return false;
}
}이진 검색 트리 빅오
최고와 평균적인 경우에,
Insertion - O(logn)
Searching - O(logn)
최악의 경우에, (요소가 백만개로 늘어났는데, 여전히 한쪽으로 치우친 트리일때)
삽입이나 탐색을 할 때 취해야 하는 단계의 숫자도 노드의 숫자 증가에 따라 커진다. ㅠ
O(n)
=> 그냥 이진 트리나 이진 탐색 트리를 사용하지 않는 것이 해결책
