문제 바로가기

접근방법

처음에 중복순열로 접근했다가 뒤늦게 n이 1000이하인걸 발견하고
아...안되겠다 하고 방향을 틀었다.
그럼 남은건 dp밖에 없는데 생각이 들었지만 dp를 잘 못하기에...다른 풀이를 보면서 공부했다.

참고 블로그

이 블로그가 이해에 많은 도움이 되었다.

이렇게 4를 만드는 경우의 수가 총 7개인데 4번 더한건 1번, 3번 더한건 3번, 2번 더한건 3번이다.

이렇게 하나하나 적어보면 규칙이 보이는데 엑셀에 정리해보면,

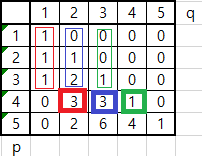
이렇게 더해가면 된다는 규칙이 나온다.
위 그림이 뭐냐면,
p를 구하기 위해 q번 덧셈을 한다는 것을 표로 나타낸 것이다.

점화식

dp[i][j] = (dp[i-1][j-1] + dp[i-2][j-1] + dp[i-3][j-1]) % 1_000_000_009 (n >= 4)

• 왜 1000000009로 나누고 나머지를 저장해야할까?
  오버플로우로 인해 정상적이지 않은 값이 들어오는 것을 방지하기 때문이라고 한다.

정답코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class s1_16195 {
    public static void main(String[] args) throws Exception{

        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));

        int n=Integer.parseInt(br.readLine());

        long[][] dp=new long[1001][1001];
        dp[1][1]=1;
        dp[2][1]=1;
        dp[2][2]=1;
        dp[3][1]=1;
        dp[3][2]=2;
        dp[3][3]=1;
        for(int i=4;i<1001;i++){
            for(int j=2;j<i;j++){
                dp[i][j]=(dp[i-1][j-1]+dp[i-2][j-1]+dp[i-3][j-1])%1000000009;
            }
            dp[i][i]=1; //1+1+1+1+1...(1로만 더한거)
        }
        for(int i=0;i<n;i++){
            StringTokenizer st=new StringTokenizer(br.readLine());
            int a=Integer.parseInt(st.nextToken());
            int b=Integer.parseInt(st.nextToken());
            long sum=0;
            for(int j=1;j<=b;j++){
                sum = (sum+dp[a][j]) % 1000000009;
            }
            System.out.println(sum);
        }
    }
}

회고

dp 너무 어렵다...
그래도 초반 값 설정해놓는것까진 생각할 수 있었는데 그 뒤로부터 생각하기 어렵다.
하나하나 손으로 적어가며 규칙을 찾자