[JAVA] 최소신장트리(MST), Kruskal 알고리즘

최소신장 트리란? (Minimum Spanning Tree)

무향 가중치 그래프에서 신장 트리를 구성하는 간선들의가중치의 합이 최소인 신장트리를 뜻한다.

kruskal 알고리즘

간선을 하나씩 선택해서 최소신장트리(MST)를 찾는 알고리즘

순서

1. 최소, 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
2. 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킨다.
   (사이클이 존재하면-> 선택하지 않고, 남아있는 간선 중 그 다음으로 가중치가 낮은 간선을 선택한다.)
3. n-1개의 간선이 선택될 때까지 2의 과정을 반복한다.
4. n-1개를 선택하면 나머지 더 볼 필요도 없다
   ∵ 가중치들을 오름차순으로 정렬해두었기 때문에

[예시]

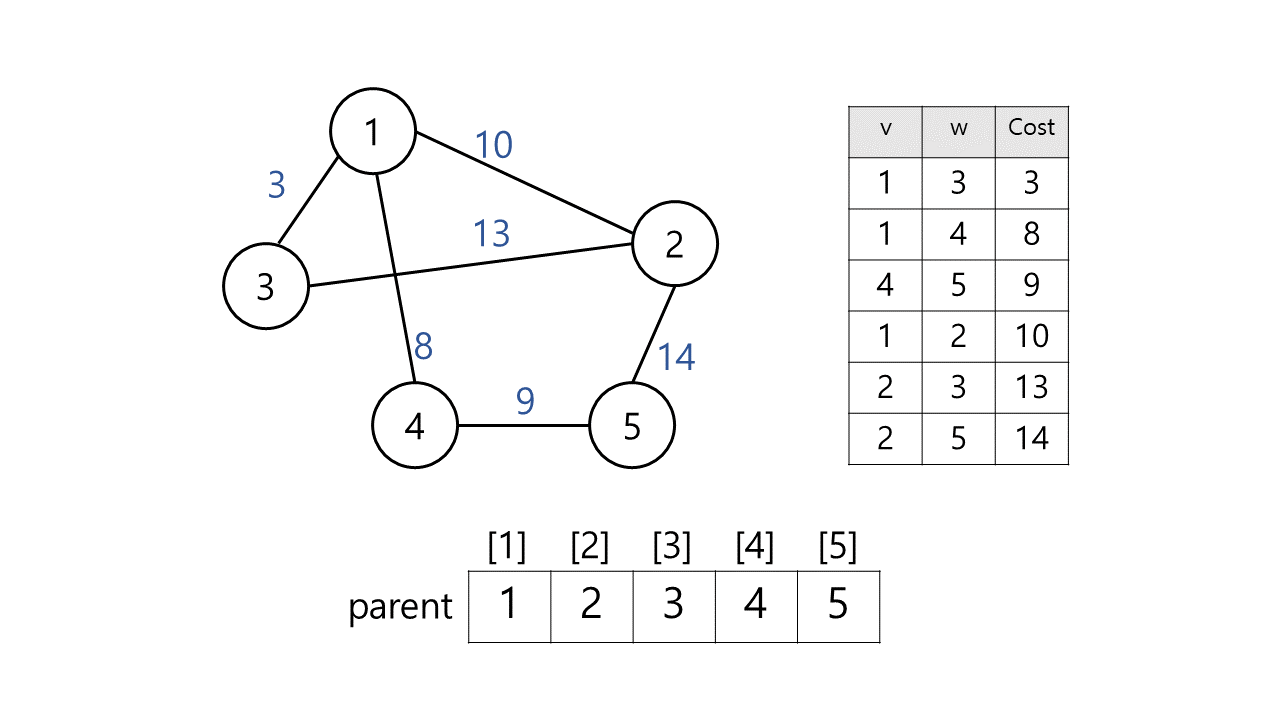
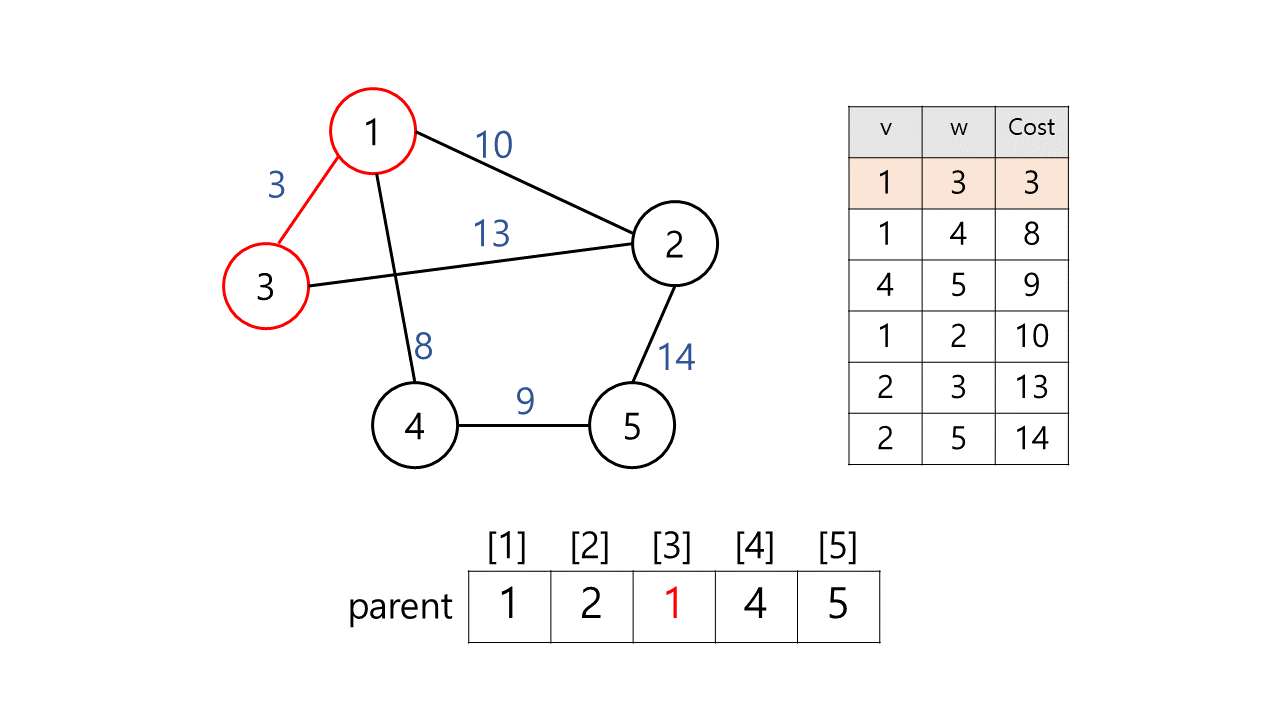
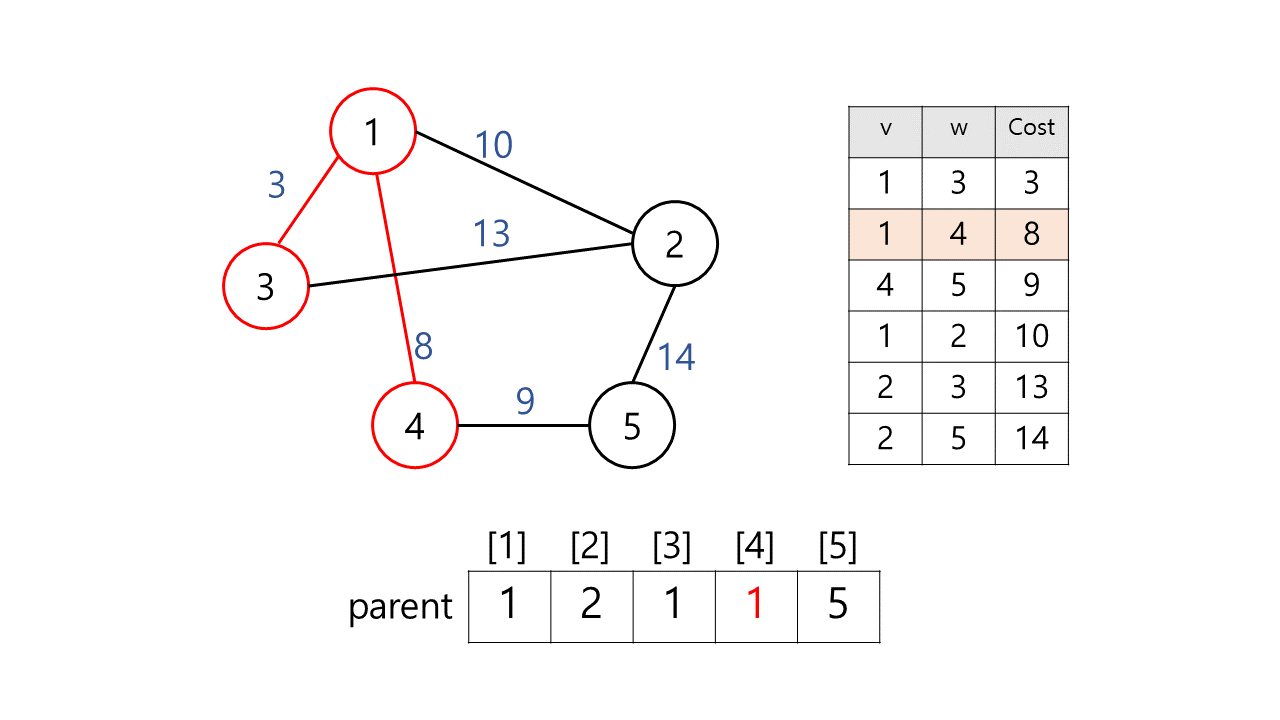
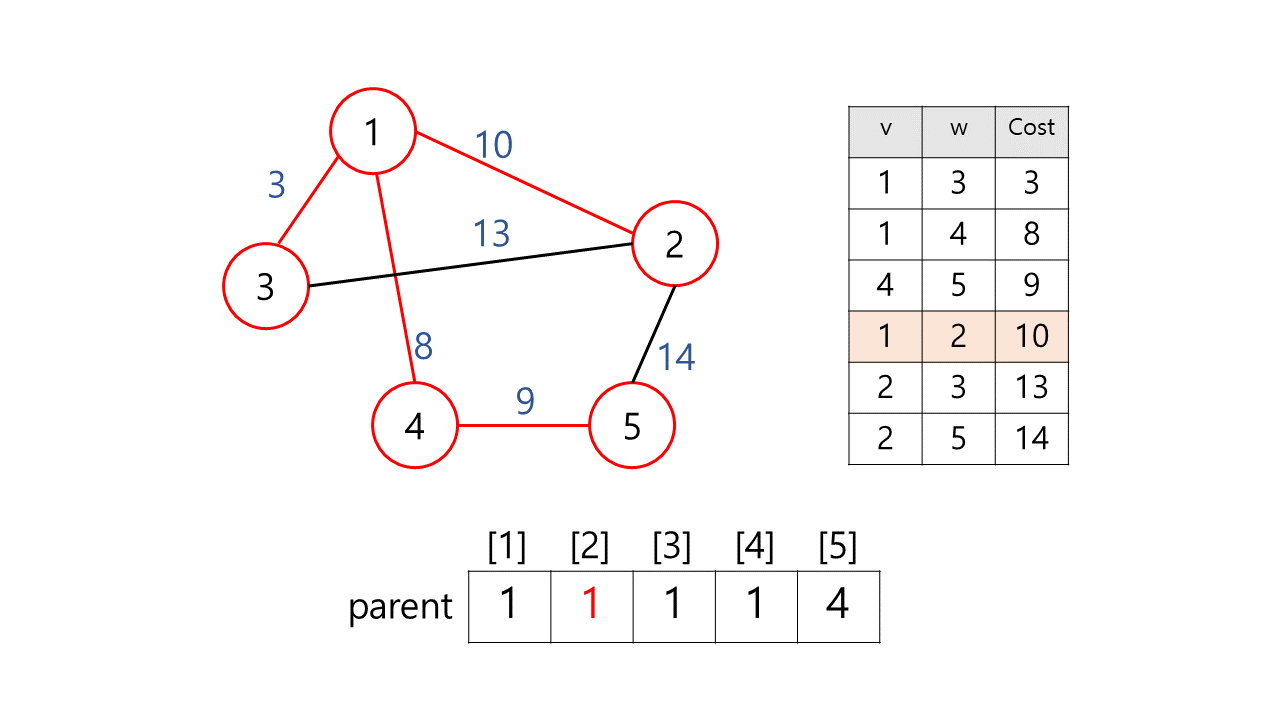
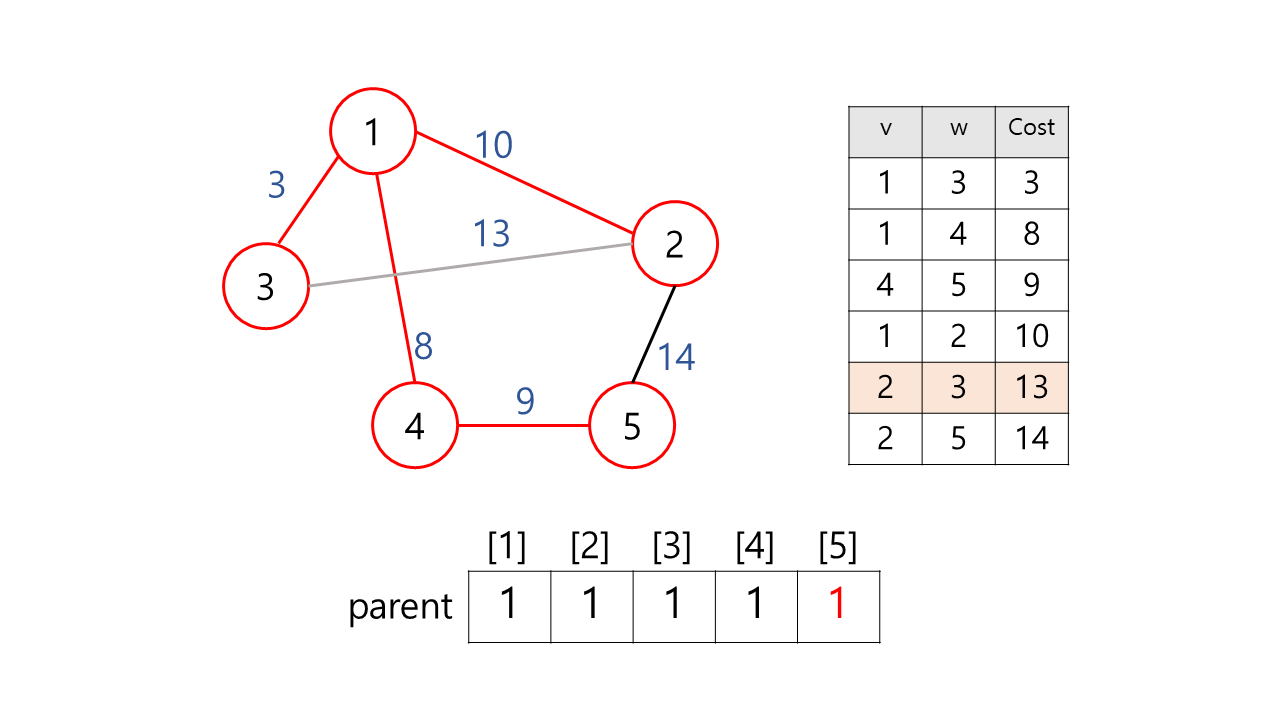
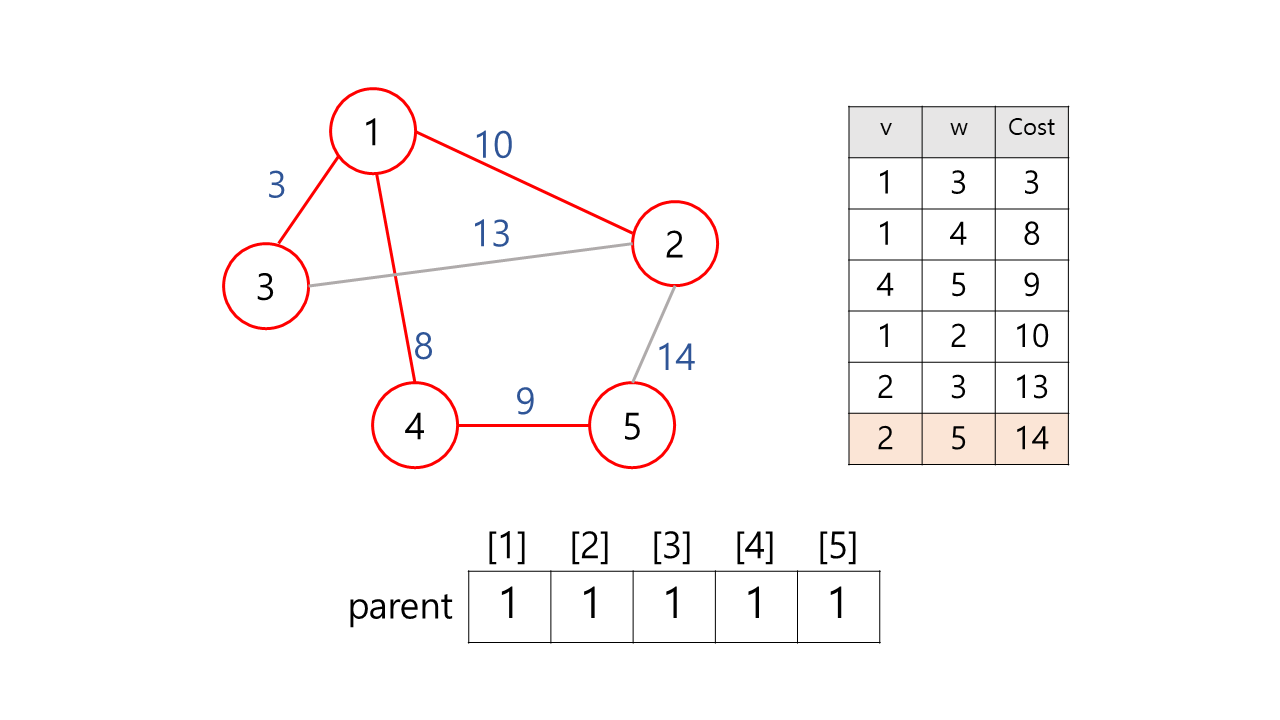
[결과]

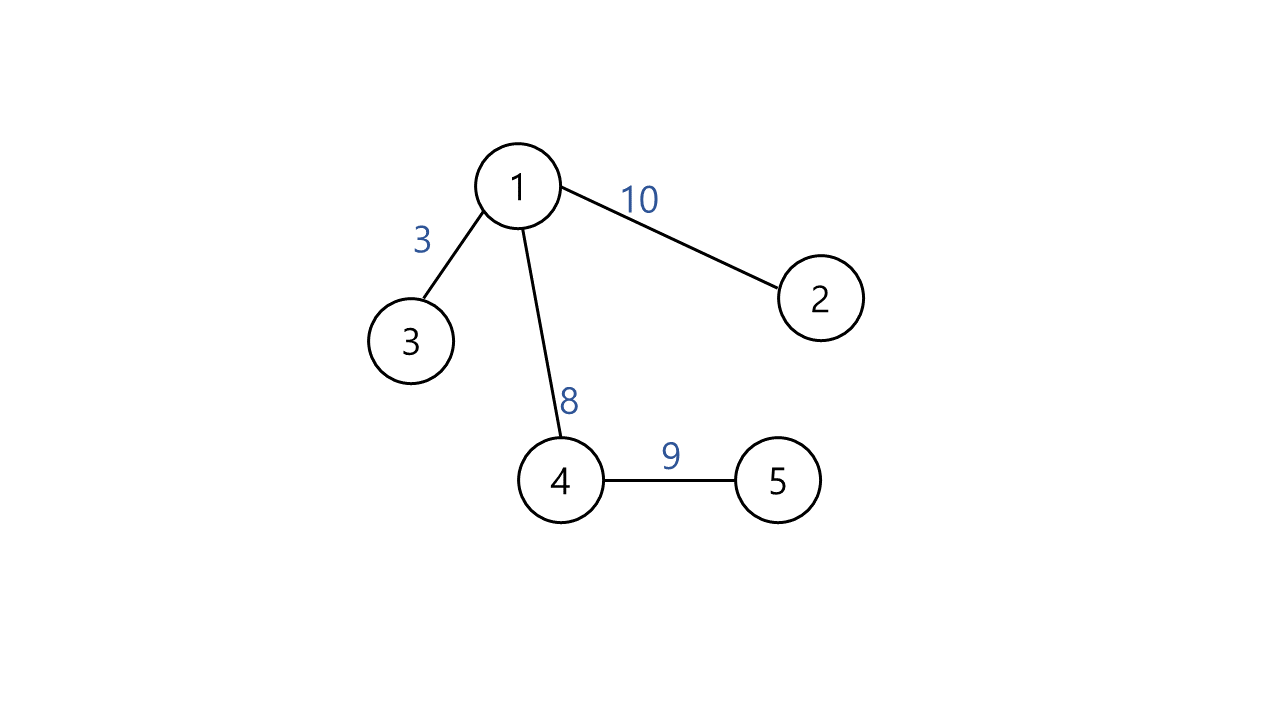
kruskal 알고리즘 구현

1. find 함수

public static int find(int [] parent, int x) {
		
		if(parent[x] ==x) return x;
		//타고타고 올라가서 최상단 부모노드를 찾자 !!
		else return parent[x] = find(parent,parent[x]);
		
	}

2. union 함수

	//union 서로소인 집합을 합치기 !!
	public static void union(int[] parent, int x, int y) {
		x = find(parent, x);
		y = find(parent, y);
		if(x<y) parent[y] = x;
		else parent[x] = y;
	}

3. kruskal

	public static void kruskal(int [][] graph, int[] parent) {	
		int cost = 0;
		//그래프를 다 돈다.
		for(int i=0; i<graph.length; i++) {
			//graph[i][0] = node1, graph[i][1] = node2, grpah[i][2] = 가중치
			//두 노드가 한집합으로 묶여있지 않다면 => 대표값(부모 값)이 같다면...
			if(find(parent,graph[i][0]) != find(parent,graph[i][1])) {
				//가중치에 넣어주자!
				cost+=graph[i][2];
				//그리고 둘을 합쳐주자!!
				union(parent, graph[i][0], graph[i][1]);
			}
		}
		System.out.println(cost);
	}

최종 사용법

package Kruskal;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class kruskal {
	
	
	//union 서로소인 집합을 합치기 !!
	public static void union(int[] parent, int x, int y) {
		
		x = find(parent, x);
		y = find(parent, y);
		
		if(x<y) parent[y] = x;
		else parent[x] = y;
	
		
	}
	
	public static int find(int [] parent, int x) {
		
		if(parent[x] ==x) return x;
		//타고타고 올라가서 최상단 부모노드를 찾자 !!
		else return parent[x] = find(parent,parent[x]);
		
	}
	

	
	public static void kruskal(int [][] graph, int[] parent) {	
		int cost = 0;
		//그래프를 다 돌거야 ...!!
		for(int i=0; i<graph.length; i++) {
			//graph[i][0] = node1, graph[i][1] = node2, grpah[i][2] = 가중치
			//두 노드가 한집합으로 묶여있지 않다면 => 대표값(부모 값)이 같다면...
			if(find(parent,graph[i][0]) != find(parent,graph[i][1])) {
				//가중치에 넣어주자!
				cost+=graph[i][2];
				//그리고 둘을 합쳐주자!!
				union(parent, graph[i][0], graph[i][1]);
			}
		}
		System.out.println(cost);
	}
	
	public static void main(String [] args) throws IOException{
		
		BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(bf.readLine());
		int m = Integer.parseInt(bf.readLine());
		int[][] graph = new int[m][3];
		
		StringTokenizer st;
		for (int i = 0; i < m; i++) {
			st = new StringTokenizer(bf.readLine());
			graph[i][0] = Integer.parseInt(st.nextToken()); // 간선 나가는 정점
			graph[i][1] = Integer.parseInt(st.nextToken()); // 간선 들어오는 정점
			graph[i][2] = Integer.parseInt(st.nextToken()); // 가중치
		}
		
		 // 간선 정렬 가중치를 기준으로 정렬한다. 
		Arrays.sort(graph, (o1, o2) -> o1[2] - o2[2]);
		
        // 부모노드 초기화 이 때 주의할 점으 ㄴn+1
		int[] parent = new int[n + 1];
		for (int i = 0; i < parent.length; i++) {
			parent[i] = i;
		}
        
		//크루스칼 알고리즘 수행
		kruskal(graph, parent);
		
	}
}