❇️ 자료구조와 알고리즘에 대해서 복기하기에 앞서서, 자료구조와 알고리즘의 개념에 대해서 톺아보자!
자료구조란 ? 🤔
데이터의 표현 및 저장방법
➕ 넓은 의미에서 int형 변수도, 구조체의 정의도 자료구조에 속한다.
뿐만 아니라, 배열을 선언해서 다양한 정보를 저장할 수 있기 때문에 배열 또한 자료구조의 일종이라고 할 수 있다.
자료구조의 분류
자료구조는 크게 선형구조와 비선형구조로 구분될 수 있다.
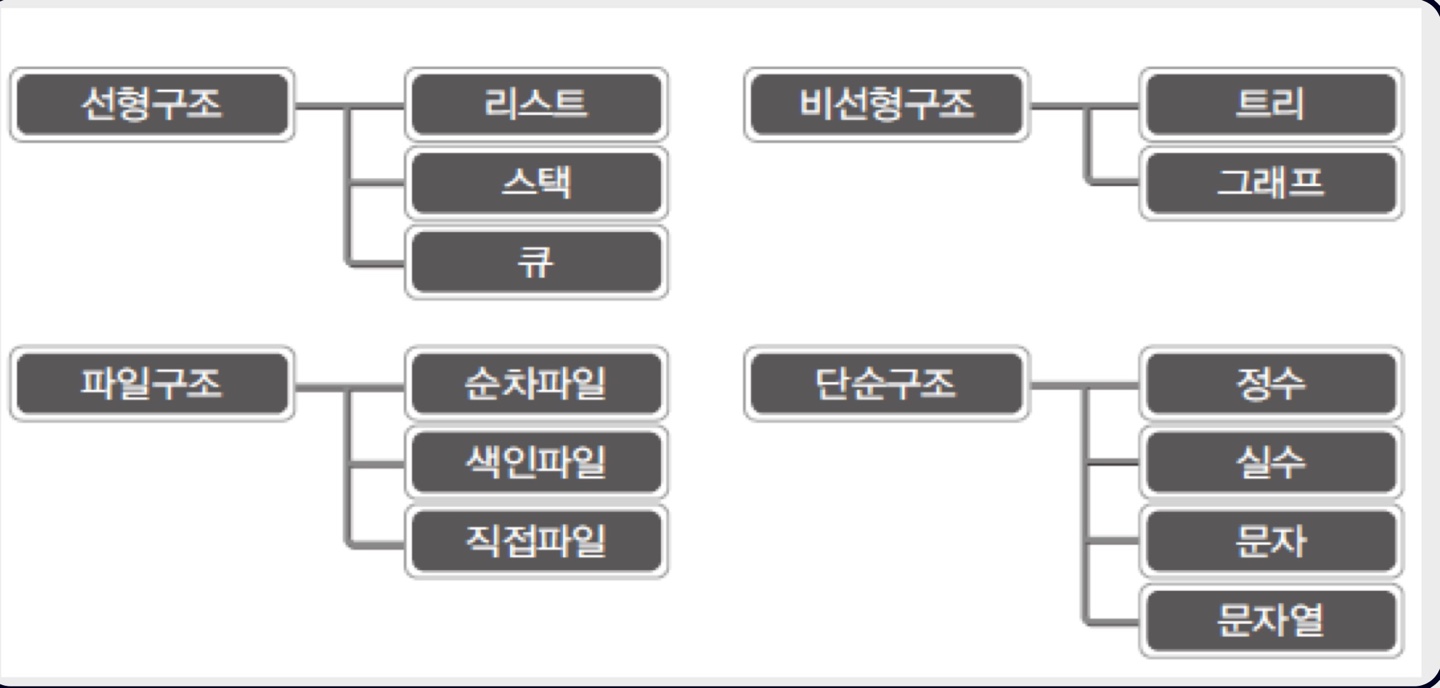
-
선형 자료구조 : 자료를 표현 및 저장하는 방식이 '션형'인 자료구조로 데이터를 선의 형태로 나란히 혹은 일렬로 저장하는 방식의 자료구조
ex ) 리스트, 스택, 큐 -
비선형 자료구조 : 자료를 표현 및 저장하는 방식이 '비선형'인 자료구조로 선형 자료구조와 다르게 데이터를 나란히 저장하지 않는 방식의 자료구조.
ex ) 트리, 그래프
알고리즘이란? 🤔
자료구조를 통해 표현 및 저장된 데이터를 대상으로 하는 '문제의 해결 방법'
프로그래머들은 효율적인 방식의 알고리즘 (문제 해결 방법)을 늘 원한다.
그렇다면 어떤 알고리즘을 선택해야 효율적일까?
를 판단하기 위해서는 알고리즘 평가기준이 필요하다.
평가 기준에는 시간복잡도, 공간복잡도가 있다.
- 시간복잡도 : 어떤 알고리즘이 어떠한 상황에서 더 빠르고 또 느리냐?
- 공간복잡도 : 어떤 알고리즘이 어떠한 상황에서 메모리를 적게 쓰고 또 많이 쓰냐?
메모리를 적게 쓰고 속도도 빨라야 최적의 알고리즘이라고 할 수 있다. 하지만 일반적으로 알고리즘을 평가할 때는 메모리의 사용량보다 실행속도에 더 초점을 둔다. 즉, 공간복잡도보다 시간복잡도에 초점을 둔다.
⚡⚡⚡
그렇다면 시간복잡도는 어떻게 구하는건가요? 🤔
연산의 횟수를 측정한다. 그리고 처리해야 할 데이터의 수 n에 대해 연산횟수의 함수 T(n)을 구성한다.
즉 알고리즘 별 연산횟수를 함수 T(n)의 형태로 구성하면, 다음 그림에서 보이는 바와 같이 그래프를 통해서 데이터의 수의 변화에 따른 연산횟수의 변화 정도를 한눈에 파악할 수 있어, 이로 인해 둘 이상의 알고리즘을 비교하기 용이해진다;
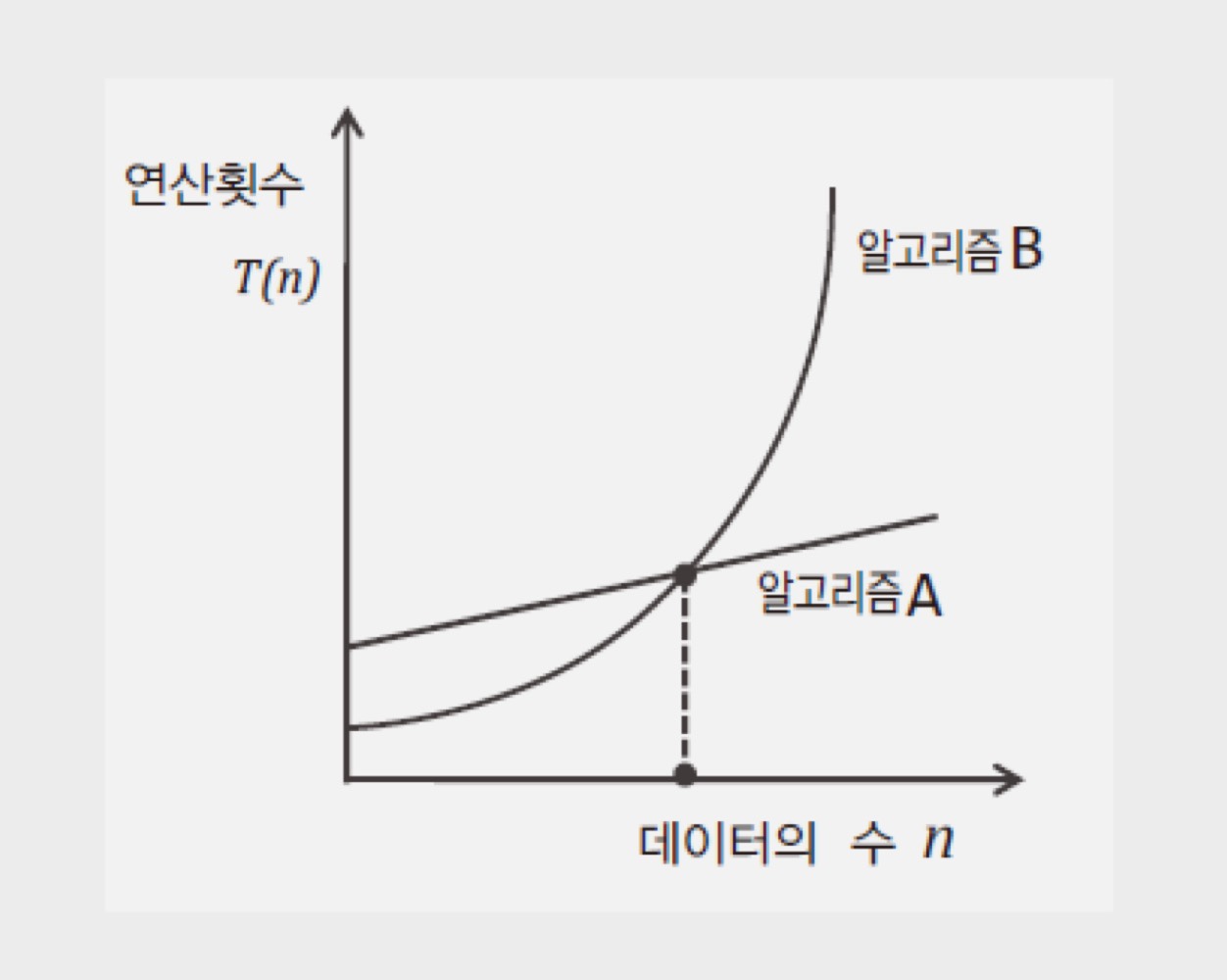
위 그래프에 따라 상황에 따라 연산횟수 즉 T(n)이 달라지기 때문에 알고리즘의 성능은 상황에 따라 평가해야한다.
그런데 말입니다...
사실 데이터의 수 n과 그에 따른 시간 복잡도 함수 T(n)을 정확히 그리고 오차 없이 구하는 것은 불가능하다.
그래서 우리는 빅-오만 따지기로 한것이다.!!
(대충 따지자는거지? 좋게 말해서 경향성을 확인하자는거 ㅎㅎ)
빅-오 표기법? 🤔
계수빼고, 뒤에 다 빼버리고 최고차항의 차수만 따지자!
빅오 란 최고차항의 차수
T(n) =
대표적인 빅-오
-
O(1)
-
O(log n)
-
O(n)
-
O(nlogn)
-
O(n^2)
-
O(n^3)
-
O(2^n)
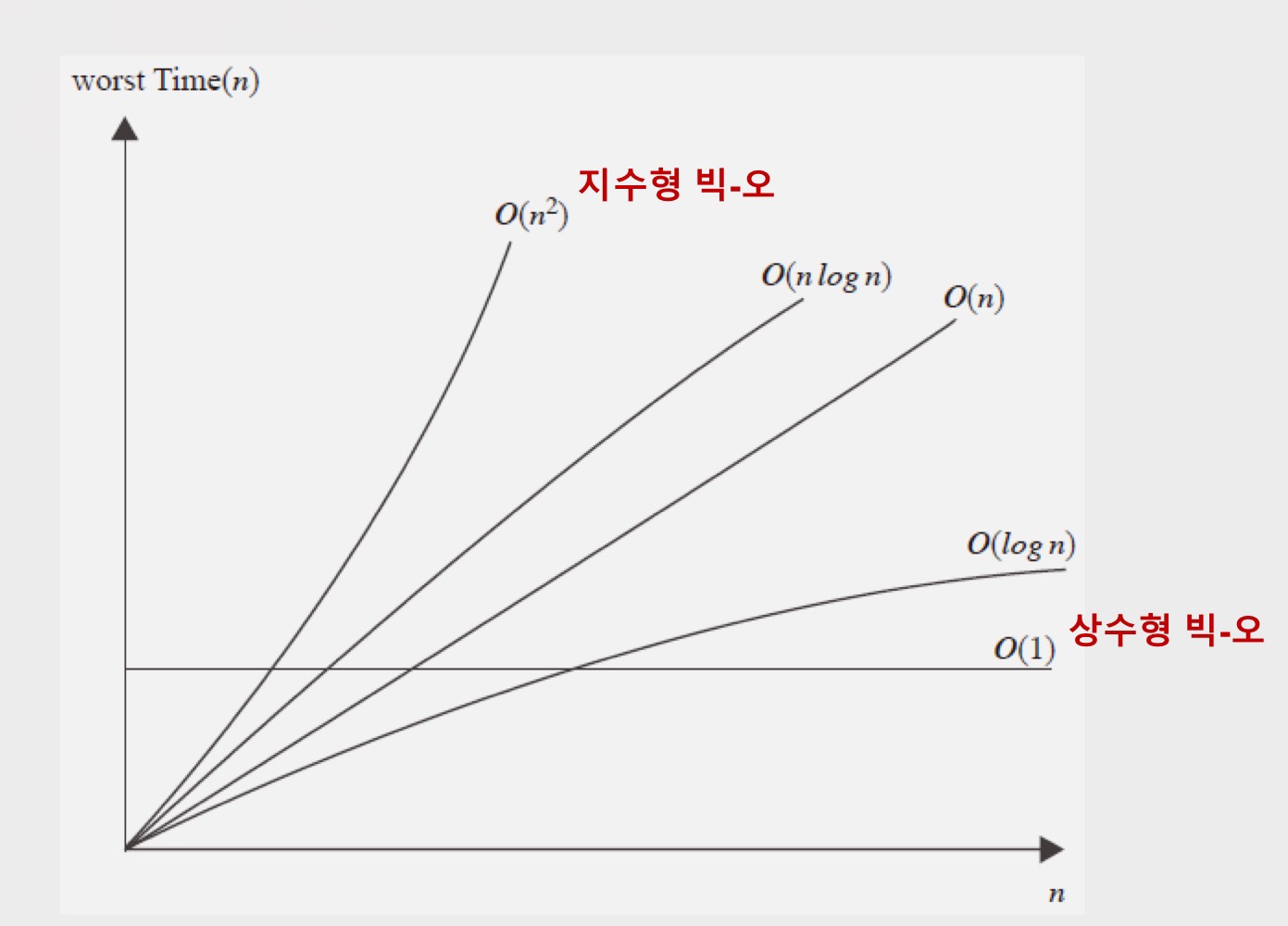
O(1)<O(log n)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)
⚡⚡⚡
위 그래프와 대소관계 기억해두면 두고두고 편합니다 🫢
