[23.02.27] Daily Coding 25 - tiling

25. tiling
    세로 길이 2, 가로 길이 n인 2 x n 보드가 있습니다. 2 x 1 크기의 타일을 가지고 이 보드를 채우는 모든 경우의 수를 리턴해야 합니다.

이런 경우의 수 문제는 일단 작은 수를 손수 계산해서 규칙을 찾아가는 것이 빠르다.

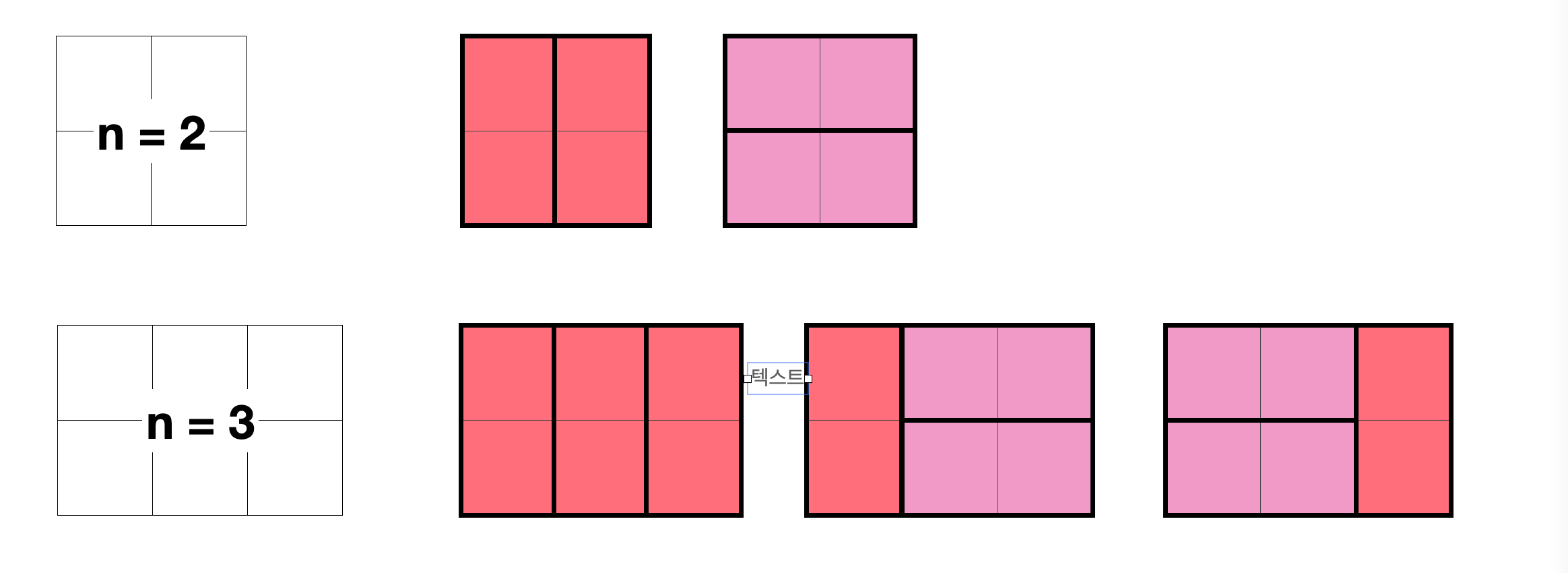
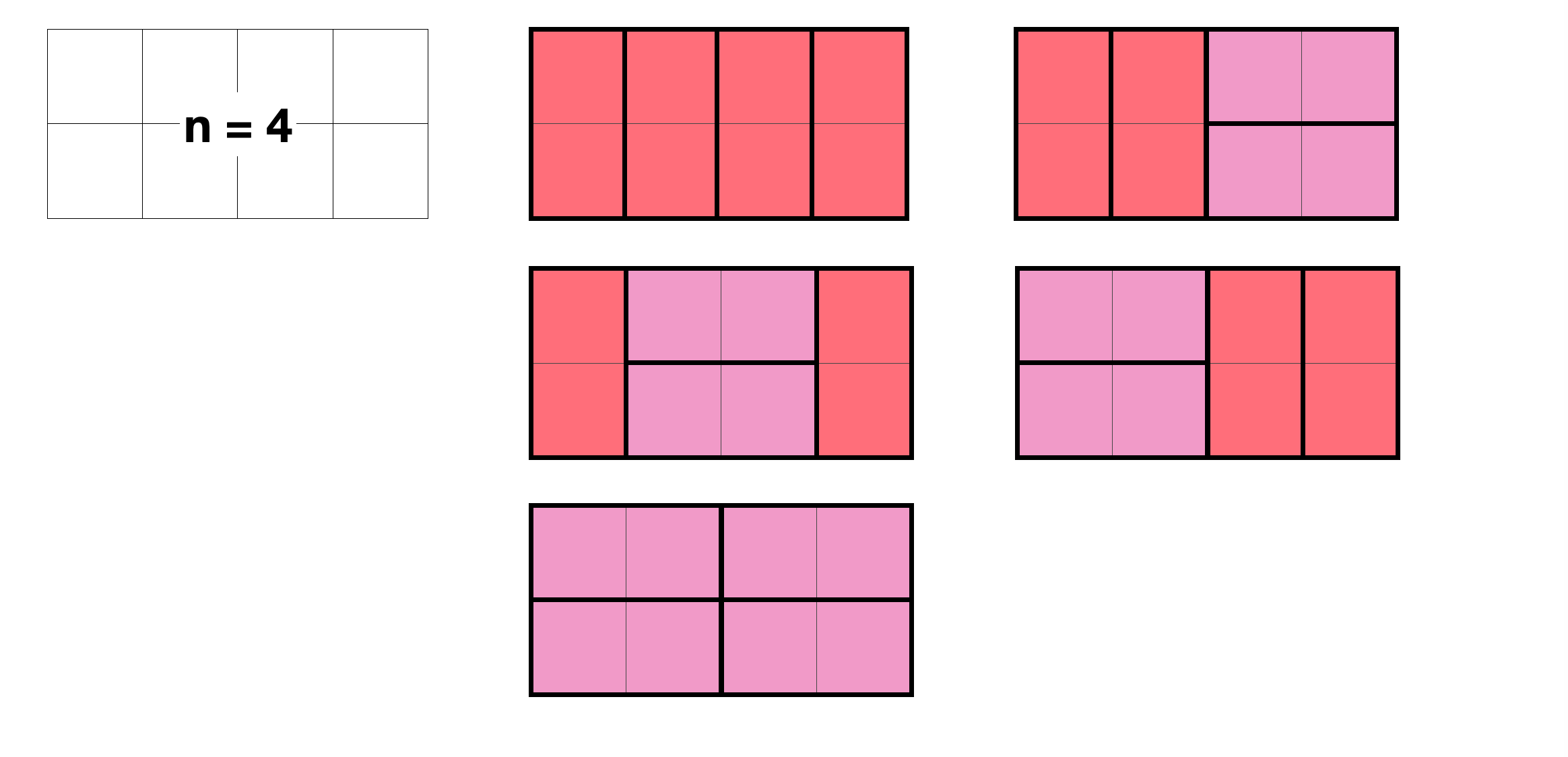
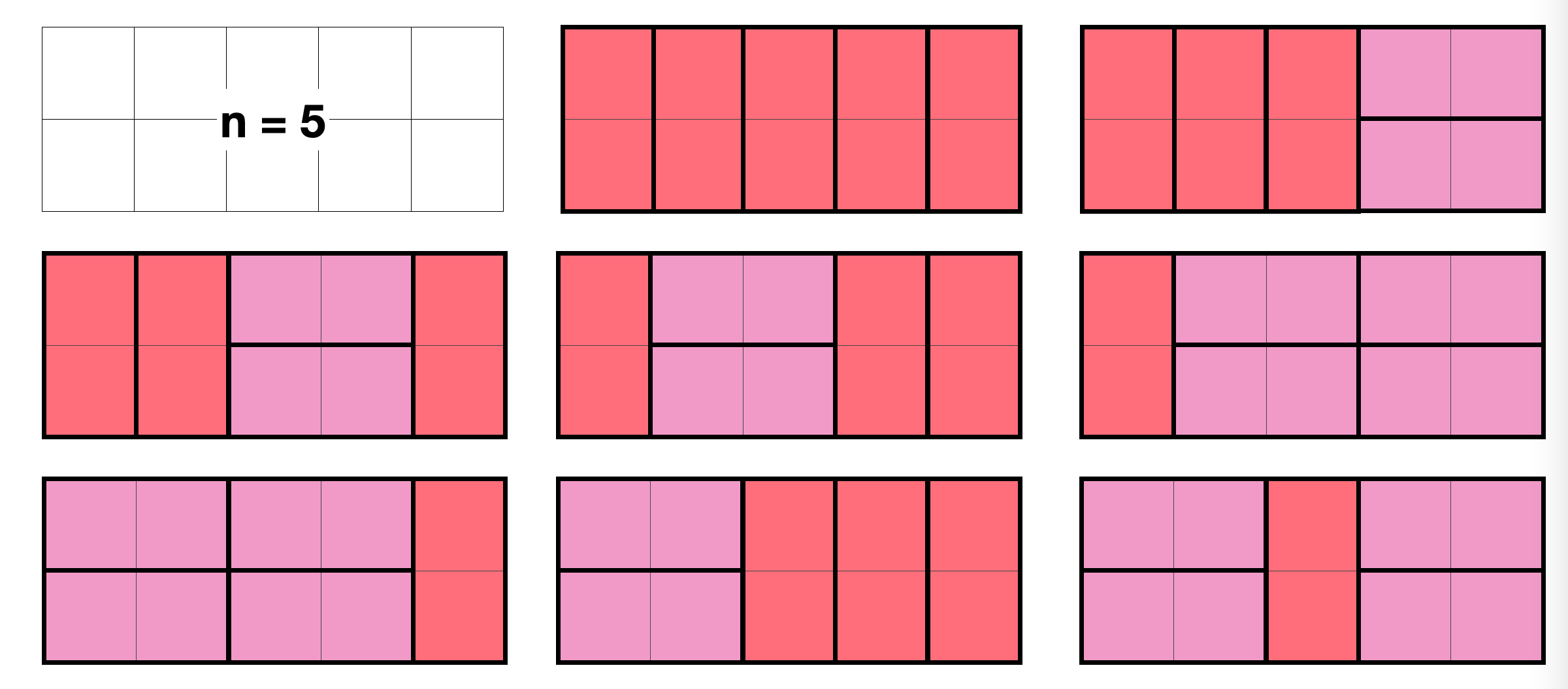
모아놓고 보니 규칙성이 보인다

n=1 -> 1
n=2 -> 2
n=3 -> 3
n=4 -> 5
n=5 -> 8
...

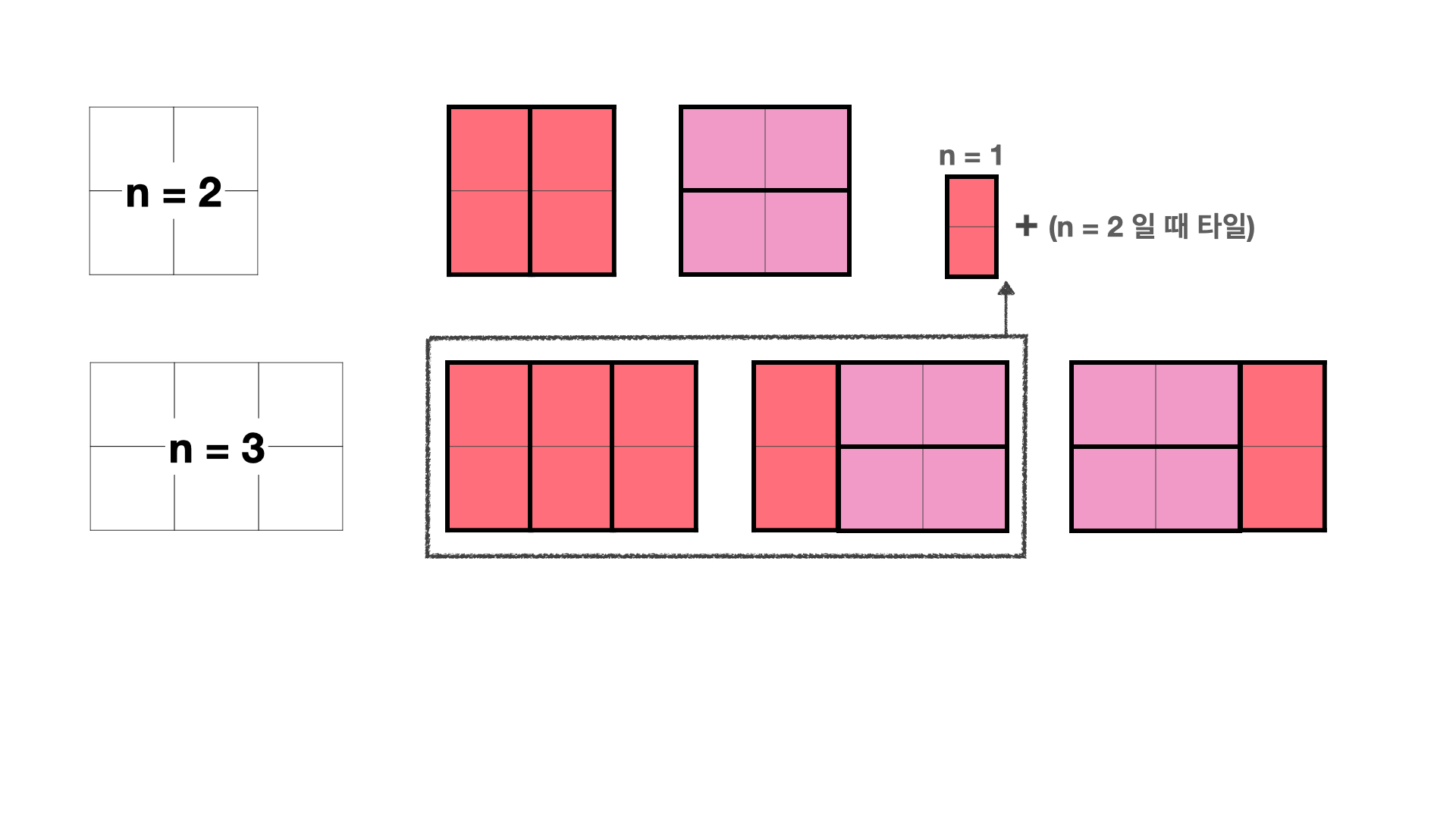
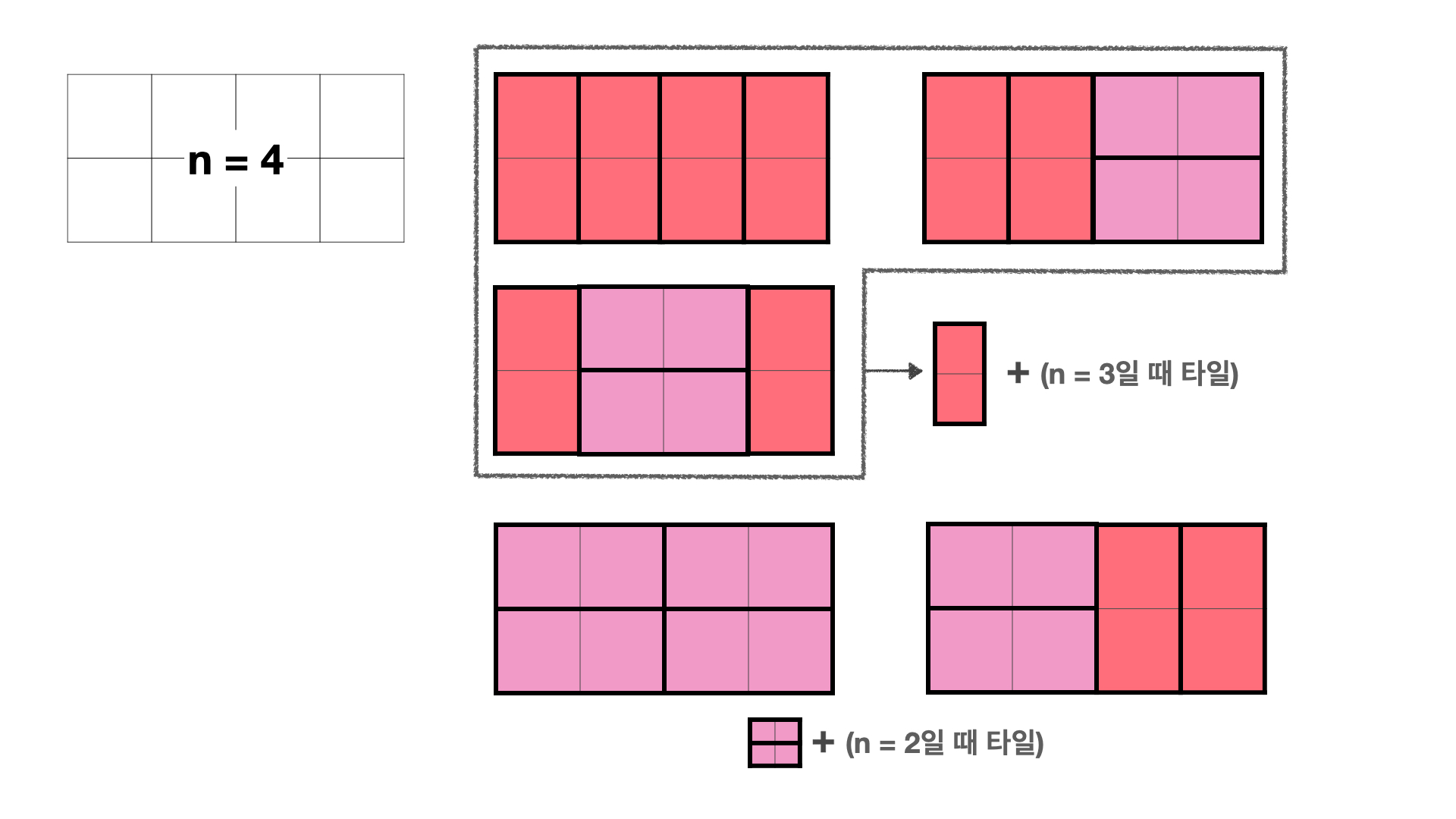
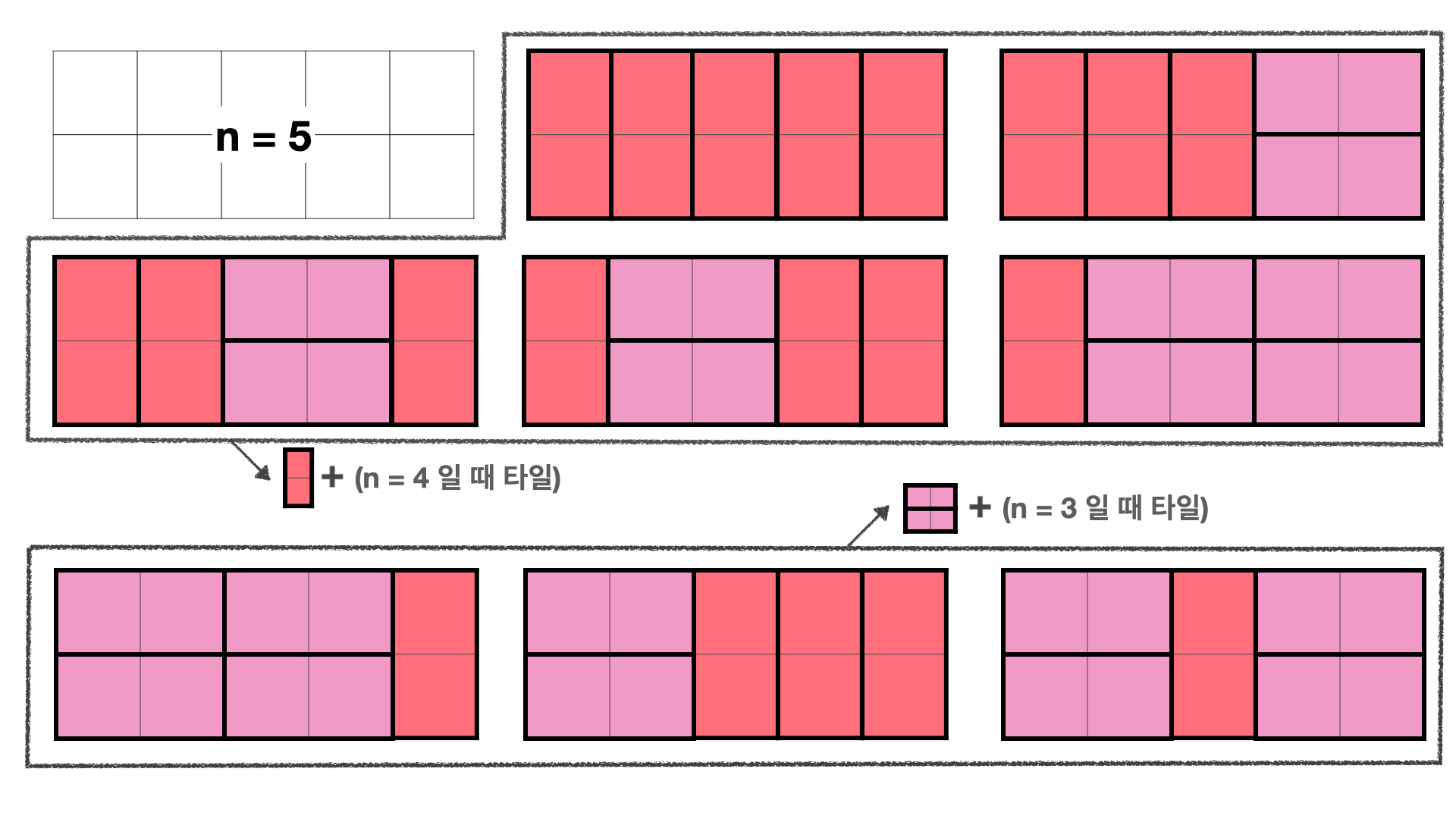
세로의 길이는 고정된 채로 가로의 길이만 늘어난 것이기 때문에,
쪼개어서 생각하면 편리하다.
결국 한 칸을 차지하는 2x1을 제외한 나머지 모양이 바로 전 (n-1)과 같고, 두 칸을 차지하는 최소 2x2를 제외한 나머지 모양이 (n-2)와 같다는 것을 알 수 있다.
즉 피보나치와 완전 유사한 수열이 되는 것.

단순한 재귀로 나타내어 보면

let tiling = function (n) {
  if (n <= 2) return n;
  return tiling(n - 2) + tiling(n - 1);
};

이렇게 되나, 이러면 저번 피보나치에서 배운 것처럼 모든 타일을 다 순회하기 때문에 시간 초과가 나온다.(피보나치,시간복잡도 줄이기 참고)

내가 쓴 답

let tiling = function (n) {

  let arr = [0,1,2];

  const boxTiling = (n) => {
    if(arr[n]) return arr[n];
    return arr[n] = boxTiling(n-1) + boxTiling(n-2);
  } 

  return boxTiling(n);
};

레퍼런스와는 조금 차이가 있었다.
나는 이미 해결한 문제를 푸는 식이었던 걸까..

레퍼런스 1 (memoization)

let tiling = function (n) {
  // 인덱스를 직관적으로 관리하기 위해
  // 앞 부분을 의미없는 데이터(dummy)로 채운다.
  const memo = [0, 1, 2];

  // 재귀를 위한 보조 함수(auxiliary function)을 선언)
  const aux = (size) => {
    // 이미 해결한 문제는 풀지 않는다.
    if (memo[size] !== undefined) return memo[size];
    if (size <= 2) return memo[n];
    memo[size] = aux(size - 1) + aux(size - 2);
    return memo[size];
  };
  return aux(n);
};

레퍼런스 2 (tabulation)

let tiling = function (n) {
  const memo = [0, 1, 2];
  if (n <= 2) return memo[n];
  for (let size = 3; size <= n; size++) {
    memo[size] = memo[size - 1] + memo[size - 2];
  }
  return memo[n];
};

레퍼런스 3 (slicing window)

let tiling = function (n) {
  let fst = 1,
    snd = 2;
  if (n <= 2) return n;
  for (let size = 3; size <= n; size++) {
    // 앞의 두 수를 더해 다음 수를 구할 수 있다.
    const next = fst + snd;
    // 다음 문제로 넘어가기 위해 필요한 2개의 데이터의 순서를 정리한다.
    fst = snd;
    snd = next;
  }
  return snd;
};

https://school.programmers.co.kr/learn/courses/30/lessons/12900

하지만!
이 세 가지 모두 시간 복잡도는 O(N) 인데...
같은 문제를 프로그래머스에 이 레퍼런스로 입력했을 때
그냥 전부 실패가 뜬다 ^^7 답이라도 맞게 해줘라

경우의 수가 많아 질 수 있으므로, 경우의 수를 1,000,000,007으로 나눈 나머지를 return해달라고 하여 그렇게 해도...

memo에 함수값을 저장할 때 나머지 연산(%1000000007)을 수행해주어도.. 몇 가지 부분에서 탈락한다. ㅠ ㅠ

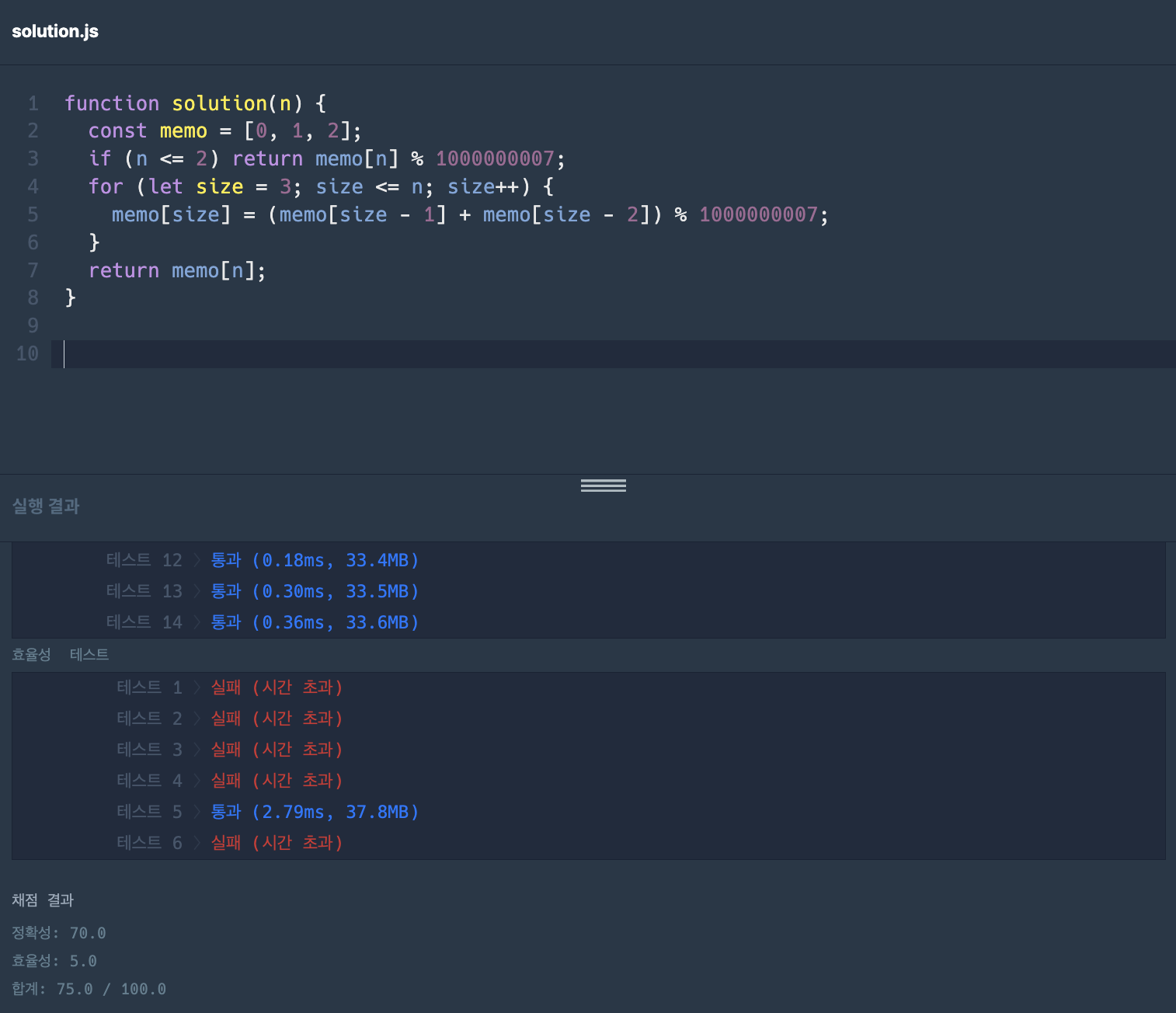
효율성이 30점 중 5점임.. ㅠ

programmers 풀이

function solution(n) {  
  const memo = [0, 1, 2];
  for (let size = 3; size <= n; size++) {
    memo[size] = (memo[size - 1] + memo[size - 2])  % 1000000007;
  }
  return memo[n];
}

우여곡절 끝에 완성한 풀이...