문제

이진트리를 다음의 규칙에 따라 행과 열에 번호가 붙어있는 격자 모양의 틀 속에 그리려고 한다. 이때 다음의 규칙에 따라 그리려고 한다.

이진트리에서 같은 레벨(level)에 있는 노드는 같은 행에 위치한다.
한 열에는 한 노드만 존재한다.
임의의 노드의 왼쪽 부트리(left subtree)에 있는 노드들은 해당 노드보다 왼쪽의 열에 위치하고, 오른쪽 부트리(right subtree)에 있는 노드들은 해당 노드보다 오른쪽의 열에 위치한다.
노드가 배치된 가장 왼쪽 열과 오른쪽 열 사이엔 아무 노드도 없이 비어있는 열은 없다.
이와 같은 규칙에 따라 이진트리를 그릴 때 각 레벨의 너비는 그 레벨에 할당된 노드 중 가장 오른쪽에 위치한 노드의 열 번호에서 가장 왼쪽에 위치한 노드의 열 번호를 뺀 값 더하기 1로 정의한다. 트리의 레벨은 가장 위쪽에 있는 루트 노드가 1이고 아래로 1씩 증가한다.

아래 그림은 어떤 이진트리를 위의 규칙에 따라 그려 본 것이다. 첫 번째 레벨의 너비는 1, 두 번째 레벨의 너비는 13, 3번째, 4번째 레벨의 너비는 각각 18이고, 5번째 레벨의 너비는 13이며, 그리고 6번째 레벨의 너비는 12이다.

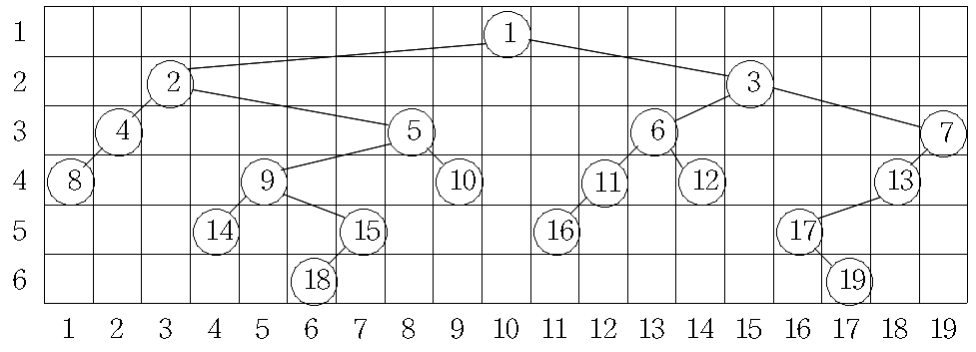
우리는 주어진 이진트리를 위의 규칙에 따라 그릴 때에 너비가 가장 넓은 레벨과 그 레벨의 너비를 계산하려고 한다. 위의 그림의 예에서 너비가 가장 넓은 레벨은 3번째와 4번째로 그 너비는 18이다. 너비가 가장 넓은 레벨이 두 개 이상 있을 때는 번호가 작은 레벨을 답으로 한다. 그러므로 이 예에 대한 답은 레벨은 3이고, 너비는 18이다.

임의의 이진트리가 입력으로 주어질 때 너비가 가장 넓은 레벨과 그 레벨의 너비를 출력하는 프로그램을 작성하시오

입력

첫째 줄에 노드의 개수를 나타내는 정수 N(1 ≤ N ≤ 10,000)이 주어진다. 다음 N개의 줄에는 각 줄마다 노드 번호와 해당 노드의 왼쪽 자식 노드와 오른쪽 자식 노드의 번호가 순서대로 주어진다. 노드들의 번호는 1부터 N까지이며, 자식이 없는 경우에는 자식 노드의 번호에 -1이 주어진다.

출력

첫째 줄에 너비가 가장 넓은 레벨과 그 레벨의 너비를 순서대로 출력한다. 너비가 가장 넓은 레벨이 두 개 이상 있을 때에는 번호가 작은 레벨을 출력한다.

예제1 - 입력

19
1 2 3
2 4 5
3 6 7
4 8 -1
5 9 10
6 11 12
7 13 -1
8 -1 -1
9 14 15
10 -1 -1
11 16 -1
12 -1 -1
13 17 -1
14 -1 -1
15 18 -1
16 -1 -1
17 -1 19
18 -1 -1
19 -1 -1

예제1 - 출력

3 18

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.StringTokenizer;

public class Main {
    static Node[] tree;
    static int maxHeight, cnt;
    static int[] maxLevel, minLevel;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());
        tree = new Node[n + 1];
        maxLevel = new int[n + 1];
        minLevel = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            tree[i] = new Node(i);
            maxLevel[i] = 0;
            minLevel[i] = n + 1;
        }

        StringTokenizer st;
        for (int i = 1; i <= n; i++){
            st = new StringTokenizer(br.readLine());
            int v = Integer.parseInt(st.nextToken());
            int l = Integer.parseInt(st.nextToken());
            int r = Integer.parseInt(st.nextToken());
            if (l != -1){
                tree[v].left = l;
                tree[l].parent = v;
            }
            if (r != -1) {
                tree[v].right = r;
                tree[r].parent = v;
            }

        }
        br.close();

        int root = 0;
        for (int i = 1; i <= n; i++) {
            if(tree[i].parent == -1){
                root = i;
                break;
            }
        }

        maxHeight = 0;
        cnt = 1;
        inorder(root, 1);

        int answer = 1;
        int diff = maxLevel[answer] - minLevel[answer] + 1;
        for (int i = 2; i <= maxHeight; i++){
            int temp = maxLevel[i] - minLevel[i] + 1;
            if (diff < temp){
                answer = i;
                diff = temp;
            }
        }
        System.out.println(answer + " " + diff);
    }
    static void inorder(int now, int height) {
        if(tree[now].left != -1){
            inorder(tree[now].left, height + 1);
        }
        maxHeight = maxHeight >= height ? maxHeight : height;
        minLevel[height] = Math.min(minLevel[height], cnt);
        maxLevel[height] = cnt;
        cnt++;
        if(tree[now].right != -1){
            inorder(tree[now].right, height + 1);
        }

    }

    static class Node {
        public int val;
        public int left = -1;
        public int right = -1;
        public int parent = -1;

        public Node(int v) {
            val = v;
        }

        public Node(int v, int left, int right){
            val = v;
            this.left = left;
            this.right = right;
        }
    }
}