유형: 그래프 탐색 (DFS)
문제: 프로그래머스 - 타겟 넘버

---

풀이

지금까지 인접 행렬, 인접 리스트의 그래프 탐색 문제만 풀다가 이런 문제도 DFS로 풀 수 있다는 것을 알게된 문제이다. 아쉽게도 혼자 해결하지 못했다. 풀이를 봐도 이해하기까지 시간이 소요됐다.

이 문제는 + 와 - 두 부호에 따라 각 숫자에서 2가지의 경우의 수를 생산한다.
이진 트리 형식으로 뻗어 나가는 문제이기 때문에 DFS로 해결할 수 있다.

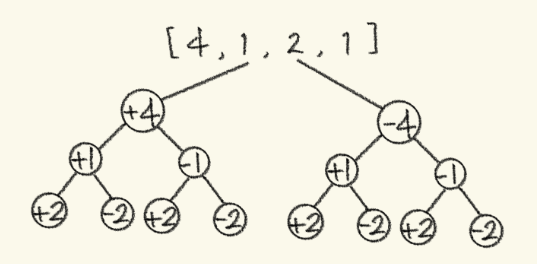
(depth=4의 그림은 생략, depth=2와 같음)

target 을 찾는 과정을 순차적으로 생각하는 게 더 헷갈렸고, 재귀적으로 생각하니 사이클이 어느정도 그려졌다.

재귀는 종료 조건과 문제 정의로 이루어진다.

종료 조건

if (depth == numbers.length) {
    if (sum == target) {
        answer++;
    }
    return;
}

depth 는 탐색을 어느 레벨까지 했는 지 알 수 있는 변수다.
마지막 노드까지 탐색한 경우, 연산 결과sum 와 target을 비교한다.

문제 정의

dfs(numbers, target, 탐색 위치, 누적된 연산 결과);

다음 탐색 위치와 지금까지 누적된 연산 결과로 다시 탐색을 한다.

위의 트리 그림을 참고해서 설명하면, 코드를 + 부터 적어놨기 때문에 왼쪽부터 쭉쭉 내려간다.
depth = 4가 돼서 결과를 비교했을 때 target과 다르다면, depth - 1레벨로 돌아가서 - 연산을 한다.
디버깅하면서 트리 흐름을 같이 따라가보면 (입출력 예 #2 기준) 종료 조건 3번째, 6번째에 target을 찾는다는 것을 알 수 있다.

---

코드

class Solution {
    static int answer = 0;
    
    public static void dfs(int[] numbers, int target, int depth, int sum) {
        if (depth == numbers.length) {
            if (sum == target) {
                answer++;
            }
            return;
        }
        
        dfs(numbers, target, depth + 1, sum + numbers[depth]);
        dfs(numbers, target, depth + 1, sum - numbers[depth]);
    }
    
    public int solution(int[] numbers, int target) {
        dfs(numbers, target, 0, 0);
        return answer;
    }
}

---

문제