
Problem Link
https://www.hackerrank.com/challenges/maximum-palindromes/problem?isFullScreen=true
✅ Problem Summary
알파벳으로 이루어진 문자열에서, 특정 구간의 문자열로 만들 수 있는 최대 길이의 팰린드롬(palindrome)의 갯수를 세는 문제 (정답은 전체 갯수에 modulo 연산을 수행한 값으로 정함)
🧮 Applied Theory & Algorithm
1. 모듈러 나눗셈 (Modular Division)
2. 페르마 소정리 (Fermat's little theorem)
- 가 정수이고 가 소수이고 일 때,
이며 일 때
이다.
💡 Idea
팰린드롬의 대칭성을 생각해보았을 때, 팰린드롬의 중앙을 기준으로 반절에 해당하는 문자열을 잘 나열하면 나머지 반절에 해당하는 문자열은 역순으로 넣어주기만 하면 된다. 따라서 이 문제를 다른 관점에서 보면, 문자열 내의 알파벳을 개수를 기준으로 반으로 나누고, 이를 나열하여 만들 수 있는 문자열의 개수를 세는 문제로 생각할 수 있다.
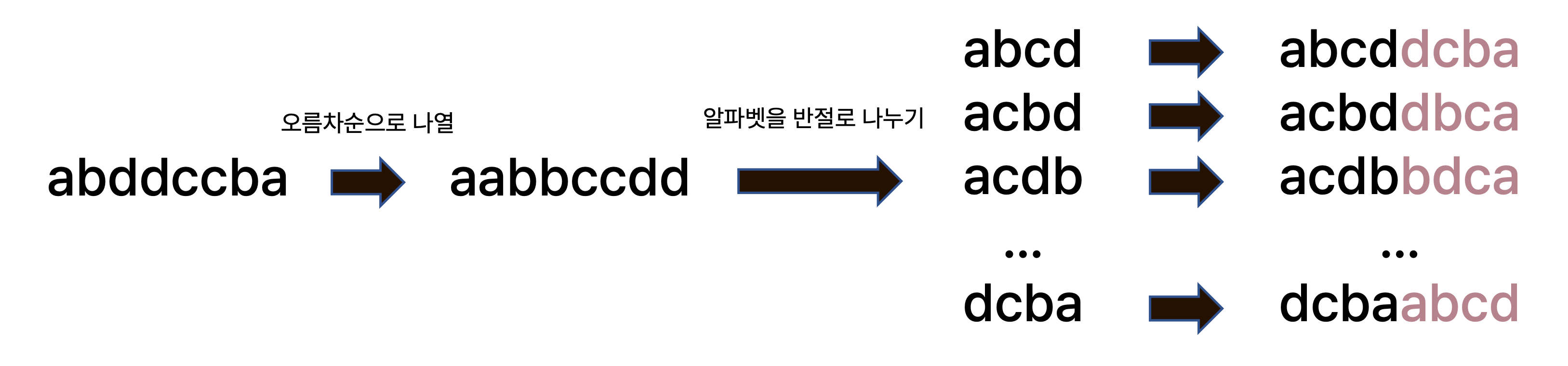
그럼 어떻게 알파벳을 나누면 될까? 우선 짝수 개인 알파벳은 문자열 어디에 위치해도 대칭성을 만족시킬 수 있기 때문에 단순하게 반으로 나누면 된다. 하지만 홀수 개인 알파벳의 경우 그냥 반으로 나누어 나열하면 팰린드롬의 대칭성을 만족시키지 못하기 때문에 다르게 처리해주어야 한다.
홀수 개의 알파벳은 알파벳이 1개인 경우와 1개 이상인 경우, 두 가지로 나눌 수 있다. 1개인 경우에는 단순히 문자열 중앙에 위치시켜주면 된다. 그럼 1개 이상인 경우에는? 홀수에서 1을 빼면 짝수가 되기 때문에, 1개를 남기고(홀수로 취급) 나머지는 짝수 개의 알파벳으로 취급해주면 된다.
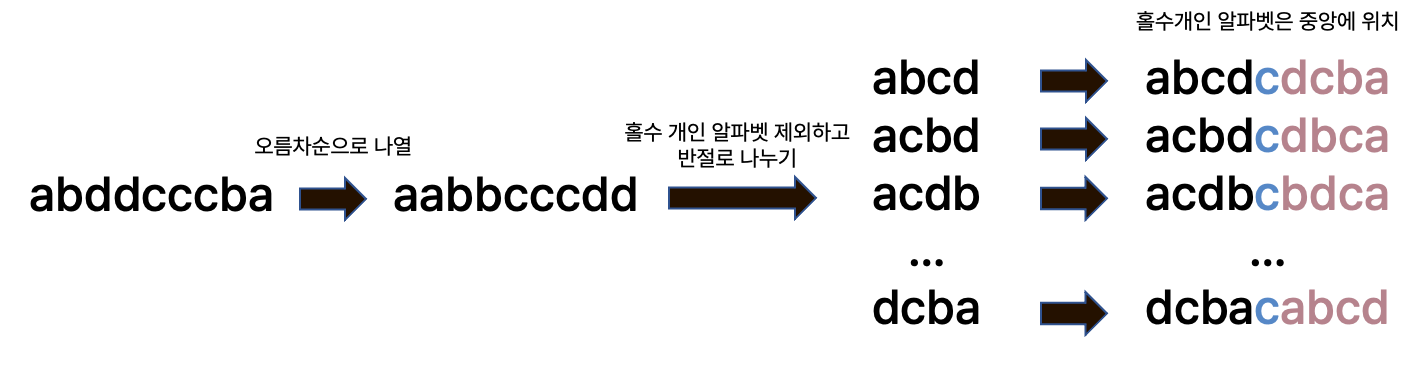
이렇게 해서 계산한 짝수, 홀수 개수를 가지고, 다음과 같이 계산해주면 가장 긴 팰린드롬의 개수를 구할 수 있다.
(짝수 개인 알파벳을 나열한 문자열의 개수) × (홀수 개인 알파벳의 개수)짝수 개인 알파벳을 나열한 문자열의 개수 는 다음 공식에 따라 계산할 수 있다. (는 문자 의 개수)
정답을 얻기 위해서 해당 값에 modulo 를 해주어야 하기 때문에 다음과 같이 식을 작성할 수 있다. (는 홀수 개인 알파벳의 개수, )
위의 식에 모듈러 나눗셈(Modular Division) 법칙을 적용해주면 최종 정답 계산식을 다음과 같이 완성할 수 있다. 모듈러 역원은 페르마의 소정리를 이용하여 구하자.
📑 My Answer
- 모든 테스트 케이스 통과
- 참고한 코드: 참고1, 참고2 - ctrs1님의 글
from collections import Counter, defaultdict
import os
factorialDict = {}
i_factorialDict = {}
cntDict = defaultdict(Counter)
m = 10 ** 9 + 7
def initialize(s):
factorialDict[0], i_factorialDict[0], cntDict[0] = 1, 1, Counter(s[0])
for i in range(1, len(s)):
factorialDict[i] = (i * factorialDict[i - 1]) % m
i_factorialDict[i] = pow(factorialDict[i], m - 2, m)
cntDict[i] = cntDict[i - 1] + Counter(s[i])
def answerQuery(l, r):
target = cntDict[r - 1] - cntDict[l - 2]
evens, odds, fact = 0, 0, 1
for v in target.values():
if v >= 2:
evens += v // 2
fact *= i_factorialDict[v // 2]
if v % 2 != 0:
odds += 1
return (max(1, odds) * factorialDict[evens] * fact) % m📌 코드 구현 설명
- 먼저 팩토리얼(factorial), 팩토리얼 역원을 계산한 값과, 문자열 내의 알파벳 개수를 저장할
initialize함수를 정의 → 연산 속도를 줄이기 위해 미리 계산initialize를 했다면,answerQuery에서 문자열 시작 지점과 끝나는 지점인l,r을 입력으로 받아, 해당 문자열 내의 있는 알파벳 개수의짝수,홀수여부를 판별하여 개수를 저장- 개수를 구했다면 💡 Idea 에서 구한 공식을 적용하여 정답을 계산
💼 Takeaway
-
모듈러 연산(Modular arithmetic), 페르마 소정리(Fermat's little theorem)의 개념과 이론을 배울 수 있었던 문제
-
수학 공식을 베이스로 한 문제들은 공식을 적용하지 않으면 효율성에서 탈락하는 경우가 발생할 수 있어서, 모든 문제에서 당황하지 않고 풀기 위해서는 PS에 사용되는 수학 이론을 많이 알아두어야 할 필요가 있어보인다.
