2.6. Probability

Eunjin Kim·2022년 4월 23일

Dive into Deep Learning

목록 보기

9/14

강의: https://d2l.ai/chapter_preliminaries/probability.html

2.6. Probability

어떤 형태로든지, 기계학습은 예측을 만드는 것이다. 우리는 환자의 임상 병력을 고려할 때 내년에 심장마비를 겪을 확률을 예측하고 싶을지도 모른다. 이상 감지에서, 우리는 비행기의 제트 엔진에서 나오는 일련의 판독값이 정상적으로 작동할 경우는 얼마나 가능성이 높은지를 평가하고자 할 수 있다. 강화 학습에서, 우리는 agent가 환경에서 지능적으로 행동하기를 원한다. 이것은 각각의 가능한 행동에서 높은 보상을 받을 가능성에 대해 생각해 볼 필요가 있다는 것을 의미한다. 그리고 추천 시스템을 구축하고자 할때도 확률을 생각해야한다. 예를 들어 우리가 대형 온라인 서점에서 일했다고 가정해보자. 어떤 책을 특정한 사용자가 살것인지에 대한 확률을 측정하고 싶을 수 있다. 이를 위해 우리는 확률의 언어를 사용할 필요가 있다. 이 챕터에서 우리는 여러분을 바닥에서 벗어나게 하고, 여러분이 첫 번째 딥러닝 모델을 만들기 시작할 수 있을 만큼만 가르치고, 여러분이 원한다면 여러분 스스로 그것을 탐구할 수 있는 주제에 대한 충분한 기회를 여러분에게 주기를 바랍니다.

우리는 이미 정확히 무엇인지 설명하거나 구체적인 예를 제시하지 않고 이전 절에서 확률을 봤었다. 첫번째 케이스를 고려함으로써 더 살펴보자: 사진을 바탕으로 고양이와 개를 구별하는 것이다. 이것은 단순하게 들릴지 모르지만, 사실 그것은 만만치 않다. 우선, 문제의 난이도는 이미지의 해상도에 따라 달라질 수 있다.

위에 사진 처럼, 사람은 160 $\times$ 160 pixels 해상도의 고양이과 개를 인지할 수 있지만, 40 $\times$ 40 pixels이면 어려워지고 10 $\times$ 10 pixels은 불가능 할 수 있다. 다시 말해서, 고양이와 개를 먼 거리에서 구별하는 우리의 능력은 (따라서 해상도가 낮은) 정보 없이 추측으로 접근할 수 있다.
확률은 우리의 확실성 수준에 대한 공식적인 추론 방법을 제공한다. 이미지가 고양이라고 확신한다면, label $y$ 가 "고양이"다( $P(y="cat")$ ) 라는 확률이 1이라는 것이다. y="cat" 또는 y="dog"이라는 제시할 증거가 없으면, 이 두 가지 가능성이 똑같이 $P(y="cat")=P(y="dog")=0.5$ 로 표현된다고 말할 수 있다. 만약 우리가 꽤 자신있지만, 그 이미지가 고양이를 묘사하고 있는지 확신하지 못했다면, $0.5<P(y="cat")<1$ 로 확률을 할당할 수 있다.

두번째 케이스를 고려해보자. 기상 관측 데이터가 주어지고, 내일 Taipei에 비가 올 확률을 예측하고 싶다. 여름이라면 0.5의 확률로 비가 올지도 모른다.

두 경우 모두 관심을 가질 가치가 있다. 그리고 두 경우 모두 결과에 대해 불확실하다. 그러나 두 사례 사이에는 중요한 차이가 있다. 첫 번째 사례에서, 그 이미지는 사실 개나 고양이 중 하나이고, 우리는 어느 것인지를 모른다. 두 번째 경우에, 만약 너가 그런 것들을 믿는다면, 그 결과는 실제로 랜덤한 것이 될 수 있다. 그래서 확률은 우리의 확실성 수준에 대한 추론을 위한 유연한 언어이고, 그것은 광범위한 맥락에서 효과적으로 적용될 수 있다.

2.6.1. Basic Probability Theory

주사위를 던졌다고 가정하고 다른 숫자가 아닌 1이 나올 확률이 얼마인지 알고 싶다고 하자. 주사위가 공정하다면, 모든 6개 결과는 동일하게 나타날 것이고, 1을 6개 경우중에 한번 볼 수 있을 것이다. 형식적으로 1은 1/6확률로 나온다라고 정의한다.

우리가 받는 진짜 주사위의 경우, 우리는 그 비율을 모를 수 있고 하자가 있는지 확인할 필요가 있을 것이다. 주사위를 조사하는 유일한 방법은 주사위를 여러 번 던지고 결과를 기록하는 것이다. 주사위를 던질 때마다, 1~6의 값을 관찰할 것이다. 이러한 결과를 고려할 때, 우리는 각 결과를 관찰할 확률을 조사하고자 한다.

자연스러운 접근 하나는, 해당 값에 대한 개별 카운트를 취하여 총 던진 수로 나누는 것이다. 이것은 우리에게 주어진 event (사건)의 확률에 대한 estimate (추정치)를 제공한다. law of large numbers 은 던지기 횟수가 증가함에 따라 이 추정치가 실제 기본 확률에 점점 더 가까워질 것이라는 것을 알려준다. 여기서 무슨 일이 일어나고 있는지 자세히 살펴보기 전에 한번 시도해 봅시다.

먼저 필요한 패키지를 import 한다.

%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l

그 다음, 우리는 주사위를 던지기를 원할 것이다. 통계학에서 우리는 확률 분포에서 예제를 도출하는 과정을 sampling 라고 부른다. 여러 이산적 선택에 확률을 할당하는 분포를 multinomial distribution 라고 한다. 나중에 분포에 대한 더 공식적인 정의를 내리겠지만, 지금은 단지 사건에 대한 확률의 할당이라고 생각하자.

단일 표본을 그리기 위해, 단순히 확률의 벡터를 전달한다. 출력은 동일한 길이의 또 다른 벡터이다: index i에서의 값은 샘플링 결과가 i에 해당하는 횟수이다.

fair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample()

# Output
tensor([0., 0., 1., 0., 0., 0.])

sampler를 실행할 때마다, 랜덤한 값이 나오는 것을 찾을 것이다. 주사위의 공정성을 추정하는 것과 마찬가지로, 우리는 종종 동일한 분포로부터 많은 샘플을 생성하기를 원한다. 파이썬의 for loop으로 하면 참을 수 없을 정도로 느리기 때문에, 우리가 사용하고 있는 함수는 우리가 원하는 어떤 형태로든 독립적인 샘플의 배열을 반환하면서 동시에 여러 개의 샘플을 그릴 수 있다.

multinomial.Multinomial(10, fair_probs).sample()

# Output
tensor([2., 1., 4., 0., 2., 1.])

이제 주사위를 굴리는것을 샘플링하는 방법을 알았으므로 1000번 롤을 시뮬레이션할 수 있다. 그런 다음 각 1000개의 롤 다음에 각 숫자가 몇 번 롤되었는지 세어 볼 수 있다. 특히, 우리는 실제 확률의 추정치로 상대적인 빈도를 계산한다.

# Store the results as 32-bit floats for division
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000  # Relative frequency as the estimate

# Output
tensor([0.1550, 0.1830, 0.1830, 0.1520, 0.1590, 0.1680])

공정한 주사위에서 데이터가 나왔기 때문에, 각각의 결과값이 실제 확률값 1/6, 거의 0.167 근처로 나온것을 알수 있다.

우리는 또한 이러한 확률들이 시간이 지남에 따라 실제 확률로 수렴하는 방법을 시각화할 수 있다. 각 그룹이 10개의 표본을 추출하는 500개의 실험 그룹을 실시한다.

counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)

d2l.set_figsize((6, 4.5))
for i in range(6):
    d2l.plt.plot(estimates[:, i].numpy(),
                 label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();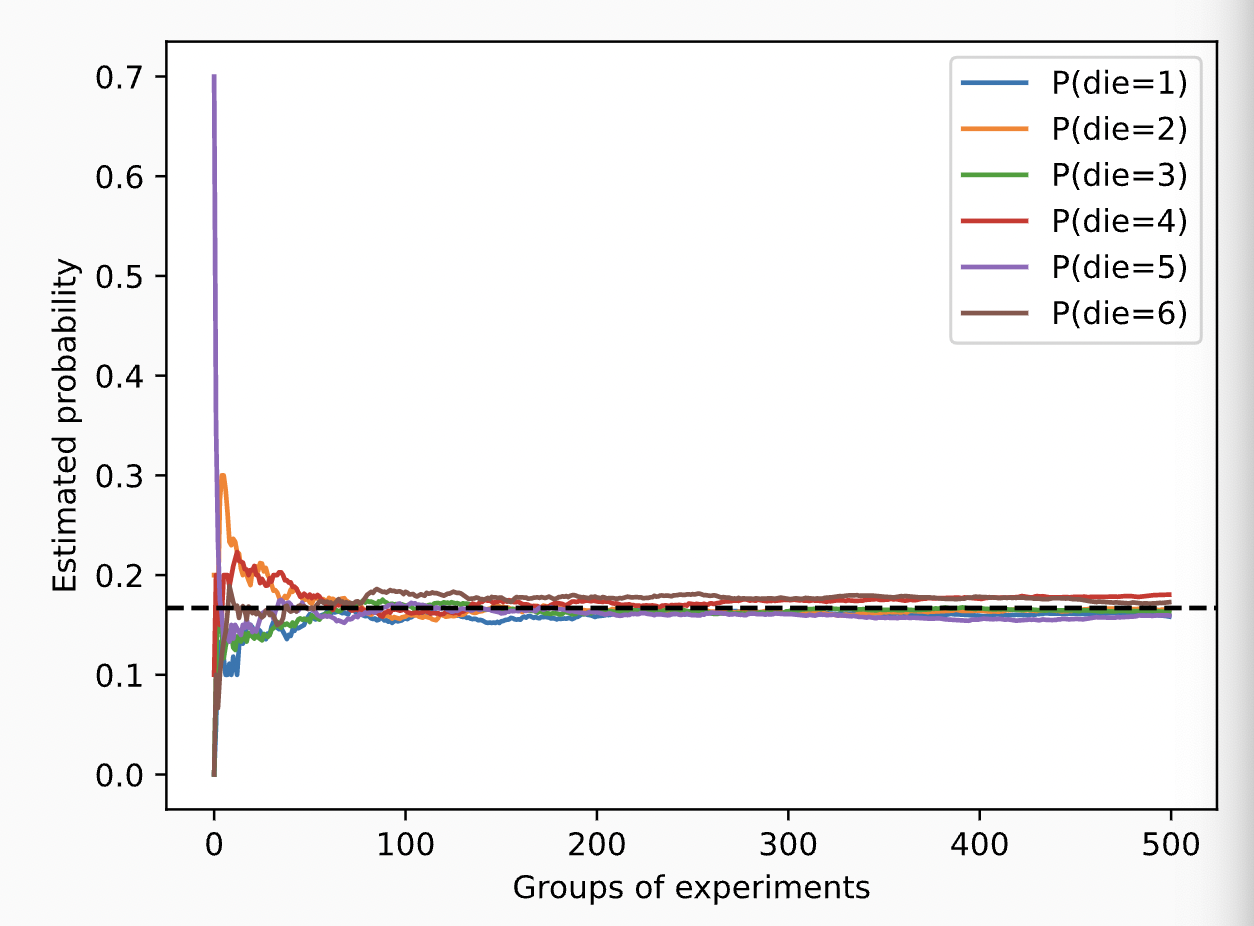

2.6.1.1. Axioms of Probability Theory

주사위 굴리기를 다룰때, 우리는 set $S={1,2,3,4,5,6}$ 을 sample space or outcome space, 각 요소들은 outcome 이라고 부른다. event 는 주어진 sample space에서 나오는 결과의 집합이다. 예를들어, '5'일 확률과 '홀수' 일 확률 둘다 주사위 굴리기에서는 유효한 event이다. 무작위 실험에서의 결과가 event $A$ 에 있다면, event $A$ 는 발생한 것이다. 즉, 주사위를 굴린 후 점 3개가 위를 향하면 '홀수일 확률' 이벤트가 발생했다고 볼 수 있다.

형식적으로, 확률 은 집합을 실제 값으로 매핑하는 함수로 생각할 수 있다. 주어진 sample space $S$ 에서 event $A$ 의 확률은, $P(A)$ 로 나타내며, 아래와 같은 속성을 가진다:

어떤 event $A$ 에서든, 확률은 음수가 아니다. $P(A) \geq 0$
전체 sample space의 확률은 1이다. $P(S)=1$
순서를 셀 수 있는 어느 $events A_1, A_2$ 든지, 어떤 일이 일어날 확률은 그들의 개별 확률의 합과 같다.

이것들은 1933년 Kolmogorov가 제안한 axioms of probability theory(확률론의 공리)이기도 하다. 이 공리 체계 덕분에, 우리는 무작위성에 대한 어떠한 철학적 논쟁도 피할 수 있다; 대신에, 우리는 수학적인 언어로 엄격하게 근거로 댈 수 있다. 예를 들어, events $A_1$ 을 전체 sample space로 놓고 $i > 1$ 에 대해 $A_i = Ø$ 이면, 우리는 $P(Ø)=0$ 을 증명할 수 있다. 가능한 이벤트의 확률은 0이다.

2.6.1.2. Random Variables

주사위 던지기 무작위 실험에서, 우리는 random variable 의 개념을 도입했다. 무작위 변수는 어느 양이든 될 수 있으며 결정되어있지 않다. 무작위 실험에서는 확률 집합 중 하나의 값을 취할 수 있다. 주사위 던지기 sample space $S={1,2,3,4,5,6}$ 에서 값을 가지는 무작위 변수 $X$ 를 고려해보자. '5를 보기'를 ${X=5} 또는 X=5$ 로 나타낼 수 있고, 그 확률은 $P({X=5}) or P(X=5)$ 로 표현한다. 그러나 이러한 지나친 규칙의 형태는 번거로운 표기법을 초래한다. 한편으로는, ompact notation의 경우, 우리는 $P(X)$ 를 임의의 변수 $X$ 에 대한 distribution(분포)로 나타낼 수 있다: distribution는 $X$ 가 어떤 값을 취할 확률을 말해준다. 반면에, $P(a)$ 를 값 a를 취할 확률로도 나타낼 수 있다. 확률 이론의 event는 표본 공간의 결과 집합이기 때문에, 우리는 임의의 변수의 값의 범위를 지정할 수 있다.

주사위의 옆면과 같은 discrete 변수와 사람의 몸무게와 키와 같은 continuous 변수 사이에는 차이가 있다는 점에 유의해라. 두 사람의 키가 정확히 같은지 묻는 것은 의미가 없다. 만약 우리가 precise enough measurements한다면, 여러분은 지구상에 정확히 같은 키를 가진 두 사람이 없다는 것을 알게 될 것이다. 사실, 만약 우리가 fine enough measurement한다면, 너는 깨어났을 때와 잠들었을 때 같은 키를 가질 수 없을 것이다. 그래서 키가 1.80139278291028719210196740527486202m일 확률은 물을 필요가 없다. 세계 인구 수를 감안할 때 확률은 사실상 0이다. 이 경우 누군가의 키가 1.79미터와 1.81미터 사이에 있는지 물어보는 것이 더 이치에 맞는다. 이러한 경우 우리는 값을 density 로 볼 가능성을 정량화한다. 정확히 1.80미터의 높이는 확률이 없지만 밀도는 0이 아니다. 서로 다른 두 높이 사이의 간격에서 우리는 0이 아닌 확률을 가진다. 이 섹션의 나머지 부분에서는 이산 공간에서의 확률을 고려한다. 연속형 랜덤 변수에 대한 확률은 section 18.6을 참조해라.

2.6.2. Dealing with Multiple Random Variables

우리는 자주 한개의 랜덤 변수보다 더 많이 고려하고 싶을 것이다. 예를 들어, 우리는 질병과 증상 사이의 관계를 모형화하기를 원할 수 있다. 질병과 증상이 주어진다면("독감"과 "기침"), 둘다 어느 정도 가능성이 있는 환자에게서 발생할 수도 있고 그렇지 않을 수도 있다. 우리는 둘의 확률이 0에 가깝기를 바라지만, 이러한 확률과 서로의 관계를 추정하여 더 나은 의료 서비스를 제공하기 위해 추론을 적용하기를 원할 수 있다.

좀 더 복잡한 예로, 이미지는 수백만 개의 픽셀이 포함되므로 수백만 개의 랜덤 변수가 포함된다. 그리고 대부분의 경우 이미지에는 이미지 내의 개체를 식별하는 label이 함께 제공된다. 우리는 label도 변수로 생각할 수 있다. 우리는 심지어 위치, 시간, ISO, 초점 거리, 카메라 유형 등과 같은 모든 메타데이터도 무작위 변수로 생각할 수 있다. 이 모든 변수는 공동으로 발생하는 랜덤 변수이다. 여러 개의 랜덤 변수를 다룰 때 몇 가지 볼 것이 있다.

2.6.2.1. Joint Probability

첫번 째는 joint probability (결합 확률) $P(A=a, B=b)$ 이다. 임의의 값 $a$ 와 $b$ 가 주어졌을 때, 결합 확률은 ' $A=a$ 와 $B=b$ 가 동시에 존재할 확률은 얼마인가?'를 대답할 수 있게 한다. 어떤 값 $a$ 와 $b$ 이든, $P(A=a, B=b) \leq P(A=a)$ 이다.

2.6.2.2. Conditional Probability

$0 \leq P(A=a, B=b)\over P(A=a) \leq 1$ , 이 ratio를 conditional probability(조건부 확률) 라 부르고 $P(B = b | A = a)$ 로 나타낸다: $A = a$ 가 발생한 경우 $B = b$ 의 확률이다.

2.6.2.3. Bayes’ theorem

조건부 확률의 정의를 사용하면 통계학에서 가장 유용하고 유명한 방정식 중 하나를 도출할 수 있다.Bayes’ theorem. 구성에 따라 multiplication rule (곱셈 규칙) $P(A, B) = P(B|A)P(A)$ 이 있다.

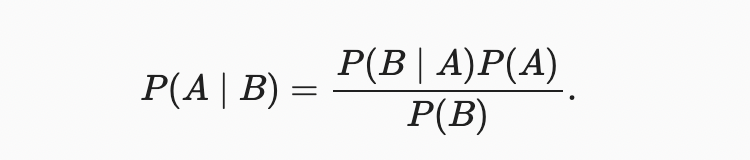
여기서 우리는 $P(A, B)$ 는 joint distribution이고 $P(A | B)$ 는 conditional distribution인 보다 compact한 표기법을 사용한다. 이러한 분포는 특정 값 X에 대해 평가할 수 있다.

2.6.2.4. Marginalization

Bayes’ theorem는 다른 것, 즉 원인과 결과를 추론하고 싶을 때 매우 유용하지만, 우리는 이 절의 뒷부분에서 볼 수 있듯이 오직 역방향의 성질만을 알고 있다. 우리가 이해하기 위해 필요한 한 가지 중요한 작업은 marginalization 이다. 이것은 $P(A, B)$ 에서 $P(B)$ 를 구하는 연산이다. 우리는 $B$ 의 확률이 $A$ 의 모든 가능한 선택을 설명하고 모든 선택들에 대한 공동 확률을 집계하는 것과 같다는 것을 알 수 있다.

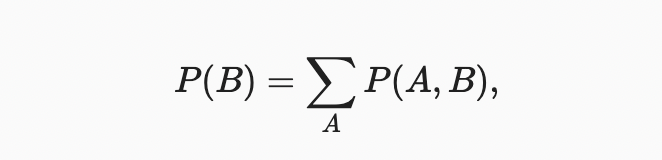
sum rule이라고도 한다. 한계화의 결과로 나타나는 확률 또는 분포를 marginal probability or a marginal distribution라고 한다.

2.6.2.5. Independence

또 다른 유용한 성질은 dependence vs. independence이다. 두 랜덤 변수 $A$ 와 $B$ 가 독립적이라는 것은 $A$ 의 한 사건이 발생해도 $B$ 의 사건 발생에 대한 어떠한 정보도 드러나지 않는다는 것을 의미한다. 이런 경우 $P(B|A)=P(B)$ 이다. 통계학자들은 $A⏊B$ 로 표현한다. Bayes’ theorem로 $P(A|B)=P(A)$ 도 바로 도출된다.

2.6.2.6. Application

우리 실력을 테스트해보자. 의사가 환자에게 HIV 검사를 시행한다고 가정한다. 이 테스트는 상당히 정확하며, 환자가 건강하지만 질병인 경우에만 1% 확률로 실패합니다. 게다가, 만약 환자가 실제로 HIV를 가지고 있다면, 반드시 HIV를 발견한다. diagnosis(양성과 음성의 경우)을 나타내는 데 D를 사용하고, HIV 상태(양성의 경우 1, 음성의 경우 0)를 나타내는 데 H를 사용한다.

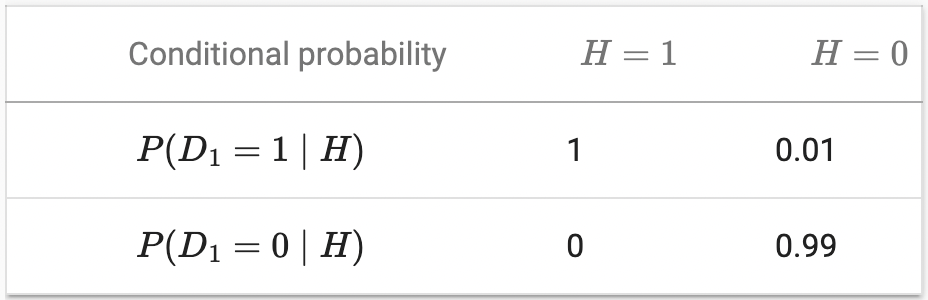
조건부 확률은 확률과 마찬가지로 최대 1까지 합해야 하므로 열 합계는 모두 1이다(행 합계는 아니다). 검사 결과가 양성으로 나올 때, 환자가 HIV에 걸릴 확률을 계산해 보자( $P(H=1|D_1=1)$ ). 분명히 이것은 그 병이 얼마나 흔한지에 달려있을 것이다. 왜냐하면 그것은 잘못된 알림 수에 영향을 미치기 때문이다. 환자들이 꽤 건강하다고 가정해보자.( $P(H=1)=0.0015$ ) Bayes’ theorem를 적용하기 위해, 우리는 marginalization와 곱셈 규칙을 적용하여

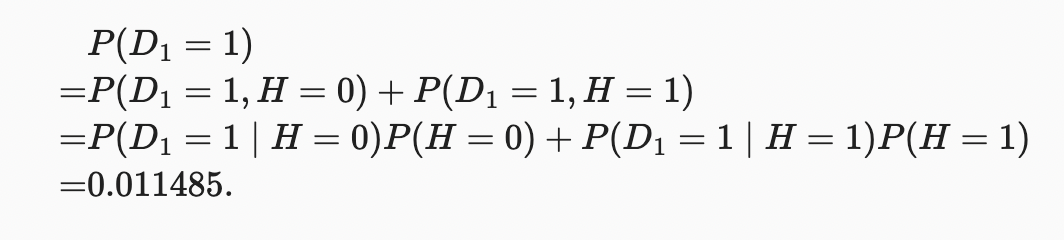
우리는 다음과 같은 결과를 얻는다.

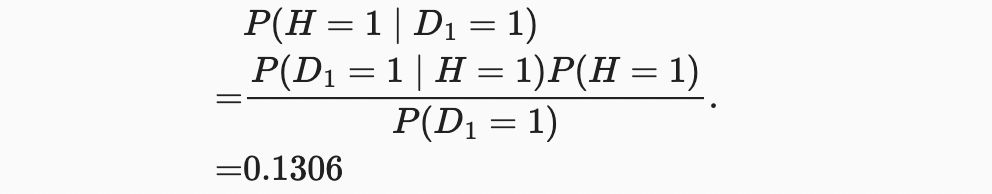
다시 말해서, 매우 정확한 검사를 사용함에도 불구하고 환자가 실제로 HIV일 확률은 13.06%에 불과하다. 우리가 알 수 있듯이, 확률은 반직관적일 수 있습니다.

이런 무서운 소식을 접한 환자는 어떻게 해야 할까? 환자가 의사에게 또 다른 테스트를 실시하여 확실성을 확보하도록 요청할 가능성이 높다. 두 번째 시험은 다른 특성을 가지고, 첫 번째 시험보다 좋지 않다.

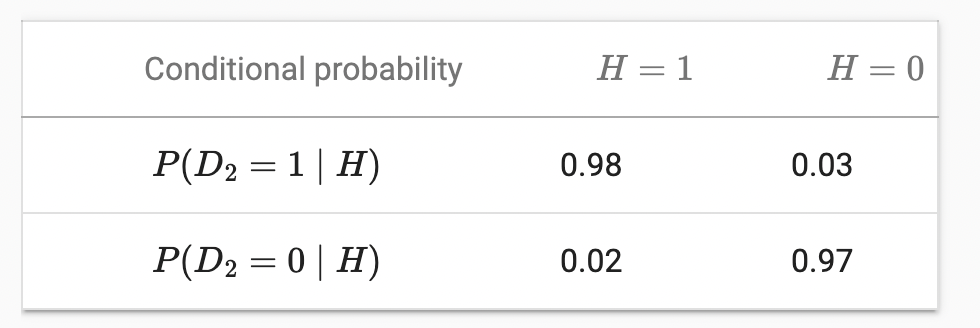
불행하게도, 두 번째 테스트도 양성으로 나타났다. 조건부 독립성을 가정하여 Bayes’ theorem를 호출하는 데 필요한 확률을 구하자.

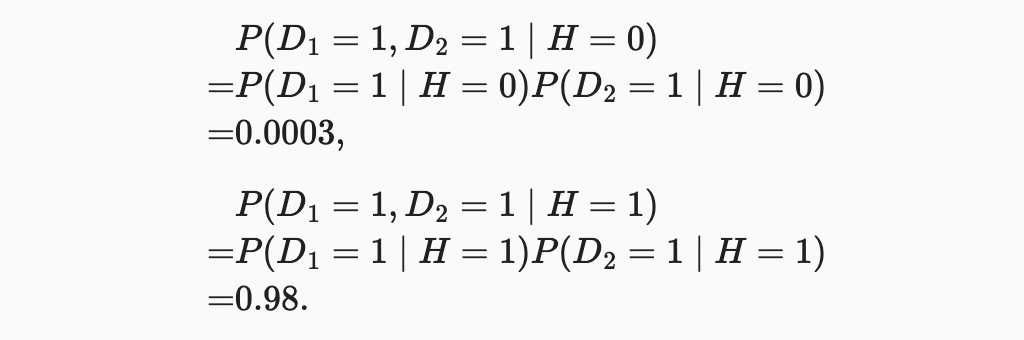
이제 marginalization와 곱셈 규칙을 적용할 수 있다.

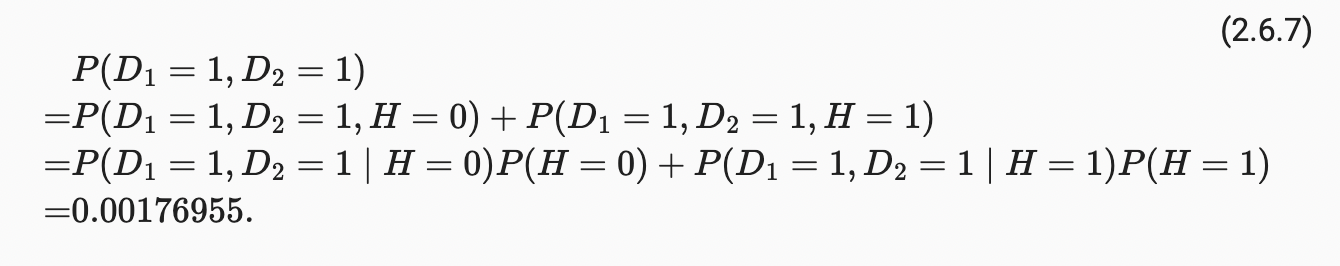
마지막으로, 환자가 두 가지 양성 반응을 보일 확률은 다음과 같다.

즉, 두 번째 테스트는 우리가 모든 것이 다 좋은 것은 아니라는 더 높은 자신감을 얻게 해주었다. 두 번째 테스트는 첫 번째 테스트보다 훨씬 덜 정확했지만, 여전히 우리의 추정치를 크게 향상시켰다.

2.6.3. Expectation and Variance

확률 분포의 주요 특성을 요약하기 위해 몇 가지 조치가 필요하다. 랜덤 변수 $X$ 의 기대치(또는 평균)는 다음과 같이 표시된다.

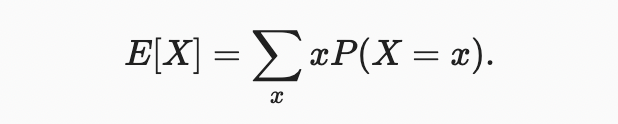
2.6.4. Summary

We can sample from probability distributions.
We can analyze multiple random variables using joint distribution, conditional distribution, Bayes’ theorem, marginalization, and independence assumptions.
Expectation and variance offer useful measures to summarize key characteristics of probability distributions.