4. 알고리즘

eunheelog·2023년 6월 7일
CS
0

boostcourse

목록 보기
7/13

boostcourse - 알고리즘

1) 검색 알고리즘

  • 배열 : 한 자료형의 여러 값들이 메모리상에 모여 있는 구조
    → 어떤 값이 배열에 속해 있는지 확인하려면 정렬 여부에 따라 아래와 같은 방법을 사용할 수 있다 !
    ① 선형 검색
    → 인덱스를 처음부터 끝까지 하나씩 증가시키며 검사
    [ 의사코드 ]

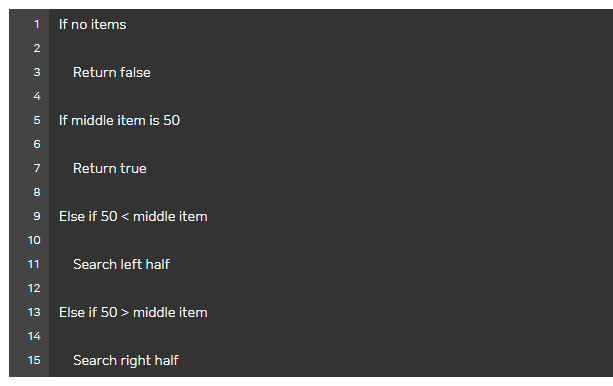
    ② 이진 검색
    → 정렬되어 있다면, 중간 인덱스부터 시작하여 찾고자 하는 값과 비교하며 그보다 작거나 큰 인덱스로 이동 !
    [ 의사 코드 ]

생각해보기-1

정렬되지 않은 배열이 있다면, 선형 검색과 이진 검색 중 빠른 것은?
→ 정렬되지 않았다면 선형검색이 더 빠를 것 같다.

2) 알고리즘 표기법

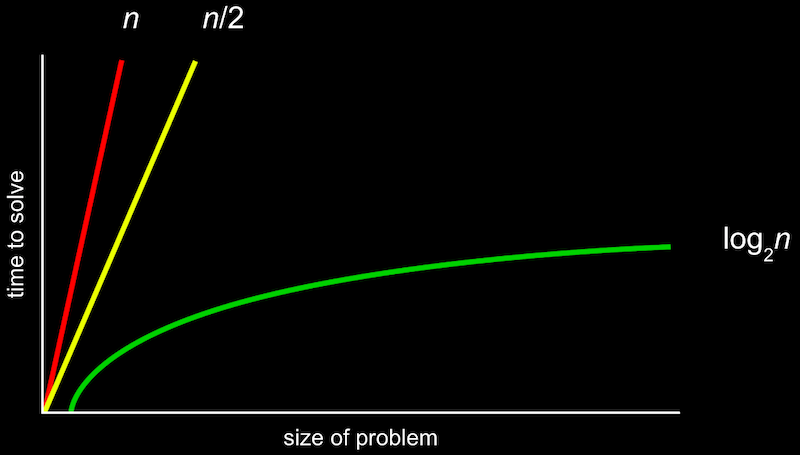
  • 위와 같은 그림을 공식적으로 표기한 것이 Big O 표기법이다.

  • 아래 목록과 같은 Big O 표기가 많이 사용된다.
    - O(n^2)
    - O(n log n)
    - O(n) ex) 선형 검색
    - O(log n) ex) 이진 검색
    - O(1)

  • Big O가 알고리즘 실행시간의 상한을 나타냄.

  • 반대로 Big Ω는 알고리즘 실행 시간의 하한을 나타낸다 !

  • 아래 목록과 같은 Big Ω 표기가 많이 사용된다.
    - Ω(n^2)
    - Ω(n log n)
    - Ω(n) - 배열 안에 존재하는 값의 개수 세기
    - Ω(log n)
    - Ω(1) - 선형 검색, 이진 검색

생각해보기-2

실행시간의 상한이 낮은 알고리즘이 좋을까요, 하한이 낮은 알고리즘이 좋을까요?
→ 상한 낮은 알고리즘이 좋다고 생각한다.
(모든 경우가 최선의 경우는 아니기에 최악의 경우를 고려해야한다.)

3) 선형 검색

: 원하는 원소가 발견될 때까지 처음부터 마지막까지 차례대로 검색
→ 모든 원소를 확인해야함.

  • 효율성 & 비효율성
    - 선형 검색 알고리즘은 정확하지만 효율적이지 못함.
    - 리스트의 길이가 n이라면 n번 실행한다.
    → 최악의 상황 : 찾고자 하는 자료가 맨 뒤에 있거나 없는 경우
    → 최선의 상황 : 처음 시도했을 때 찾는 경우
    → 평균적으로 선형 검색이 최악의 상황에서 종료되는 것에 가깝다고 가정할 수 있다.
    ∴ 자료가 정렬되어 있지 않거나 어떤 정보도 없어 하나씩 찾아야하는 경우에 유용하다 !

SourceCode - 선형검색

#include <cs50.h>
#include <stdio.h>

int main(void)
{
    // numbers 배열 정의 및 값 입력
    int numbers[] = {4, 8, 15, 16, 23, 42};

    // 값 50 검색
    for (int i = 0; i < 6; i++)
    {
        if (numbers[i] == 50)
        {
            printf("Found\n");
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

SourceCode
(특정 이름을 찾아 해당 전화번호 출력)

#include <cs50.h>
#include <stdio.h>
#include <string.h>

int main(void)
{
    string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"};
    string numbers[] = {"617–555–0100", "617–555–0101", "617–555–0102", "617–555–0103"};

    for (int i = 0; i < 4; i++)
    {
        if (strcmp(names[i], "EMMA") == 0)
        {
            printf("Found %s\n", numbers[i]);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

→ names 배열과 numbers 배열이 서로 같은 인덱스를 가져야한다는 한계 발생.

SourceCode
↓구조체를 정의하여 이름과 번호를 묶음

#include <cs50.h>
#include <stdio.h>
#include <string.h>

typedef struct
{
    string name;
    string number;
}
person;

int main(void)
{
    person people[4];

    people[0].name = "EMMA";
    people[0].number = "617–555–0100";
    people[1].name = "RODRIGO";
    people[1].number = "617–555–0101";
    people[2].name = "BRIAN";
    people[2].number = "617–555–0102";
    people[3].name = "DAVID";
    people[3].number = "617–555–0103";

    // EMMA 검색
    for (int i = 0; i < 4; i++)
    {
        if (strcmp(people[i].name, "EMMA") == 0)
        {
            printf("Found %s\n", people[i].number);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

→ person a; 라는 변수가 있다면, a.name 또는 a.number으로 이름과 전화번호를 저장

생각해보기-3

전화번호부와 같이 구조체를 정의하여 관리 및 검색을 하면 더 편리한 예는 또 무엇이 있을까요?
→ 고객이나 학생들의 정보

4) 버블 정렬

: 두 개의 인접한 자료 값을 비교하면서 위치를 교환

  • 하나의 요소를 정렬하기 위해 낭비가 발생할 수 있다.
    [ 의사 코드 ]
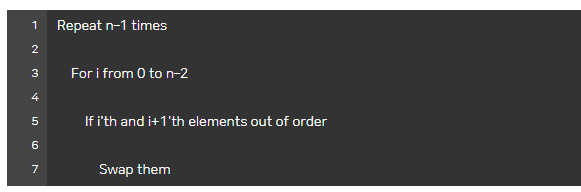
  • 상한과 하한은 Ω(n^2)이다.

생각해보기-4

버블 정렬이 효율적인 경우는 어떤 경우인가요? 반대로 어떤 경우에 비효율적이게 될까요?
→ 정렬이 되어있지 않을 경우에 효율적이고, 하나의 원소의 위치를 바꿔야하거나 이미 정렬되어있는 경우에 비효율적이다.

5) 선택 정렬

: 배열 안의 자료 중 가장 작은 수(or 가장 큰 수)를 찾아 첫 번째 위치(or 가장 마지막 위치)의 수와 교환

  • 교환 횟수는 감소, 비교 횟수는 증가
    [ 의사 코드 ]
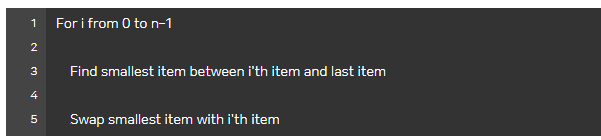
  • 두 번의 루프를 돌아야한다.
  • 상한과 하한은 Ω(n^2)이다.

생각해보기-5

선택 정렬을 좀 더 효율적으로 어떻게 바꿀 수 있을까요?
→ 순서대로 가장 작은 수를 찾아 다른 배열에 저장한다.

6) 정렬 알고리즘의 실행시간

  • 실행시간의 상한
    - O(n^2) : 선택 정렬, 버블 정렬
    - O(n log n)
    - O(n) : 선형 검색
    - O(log n) : 이진 검색
    - O(1)

  • 실행시간의 하한
    - Ω(n^2) : 선택 정렬, 버블 정렬
    - Ω(n log n)
    - Ω(n)
    - Ω(log n)
    - Ω(1) : 선형 검색, 이진 검색

  • 버블 정렬을 효율적으로 하는 방법
    (정렬이 되어있는 숫자 리스트가 주어짐)
    [ 의사 코드 ]

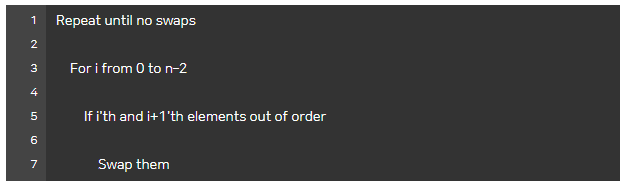
    → 최종적으로 버블 정렬의 하한은 Ω(n)이 된다.

  • 실행시간의 하한
    - Ω(n^2) : 선택 정렬, 버블 정렬
    - Ω(n log n)
    - Ω(n) : 버블 정렬
    - Ω(log n)
    - Ω(1) : 선형 검색, 이진 검색

생각해보기-6

선택 정렬의 실행 시간의 하한도 버블 정렬처럼 더 단축 시킬 수 있을까요?
→ 모든 배열을 확인해야하기 때문에 어려울 것 같다.

7) 재귀

SourceCode

#include <cs50.h>
#include <stdio.h>

void draw(int h);

int main(void)
{
    // 사용자로부터 피라미드의 높이를 입력 받아 저장
    int height = get_int("Height: ");

    // 피라미드 그리기
    draw(height);
}

void draw(int h)
{
    // 높이가 h인 피라미드 그리기
    for (int i = 1; i <= h; i++)
    {
        for (int j = 1; j <= i; j++)
        {
            printf("#");
        }
        printf("\n");
    }

SourceCode
(중첩 루프 없애고 재귀함수 호출)

#include <cs50.h>
#include <stdio.h>

void draw(int h);

int main(void)
{
    int height = get_int("Height: ");

    draw(height);
}

void draw(int h)
{
    // 높이가 0이라면 (그릴 필요가 없다면)
    if (h == 0)
    {
        return;
    }

    // 높이가 h-1인 피라미드 그리기
    draw(h - 1);

    // 피라미드에서 폭이 h인 한 층 그리기
    for (int i = 0; i < h; i++)
    {
        printf("#");
    }
    printf("\n");
}

생각해보기-7

반복문을 쓸 수 있는데도 재귀를 사용하는 이유는 무엇일까요?
→ 가독성이 좋고 큰 문제를 작은 문제로 나누어 해결할 수 있기 때문이라고 생각한다.

8) 병합 정렬

: 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합치면서 정렬

  • 병합 정렬 실행 시간의 상한은 O(n log n)
    → 숫자들을 반으로 나누는 데 O(log n), 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)
  • 실행 시간의 하한도 Ω(n log n)
    → 정렬 여부에 상관없이 나누고 병합하는 과정을 거치기 때문

생각해보기-8

병합 정렬을 선택 정렬이나 버블 정렬과 비교했을 때 장점과 단점은 무엇이 있을까요?
→ 속도가 빠르다는 장점과 메모리가 추가적으로 필요하다는 단점이 있다.

profile
eunheelog
⛧1일 1알고리즘⛧
이전 포스트

Quiz 3

다음 포스트

Quiz 4

0개의 댓글