[JS] LV.2 피보나치 수

프로그래머스 레벨 2단계 '피보나치 수' 문제 풀기

문제 설명

피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다.

예를들어

• F(2) = F(0) + F(1) = 0 + 1 = 1
• F(3) = F(1) + F(2) = 1 + 1 = 2
• F(4) = F(2) + F(3) = 1 + 2 = 3
• F(5) = F(3) + F(4) = 2 + 3 = 5

와 같이 이어집니다.

2 이상의 n이 입력되었을 때, n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴하는 함수, solution을 완성해 주세요.

제한 사항

• n은 2 이상 100,000 이하인 자연수입니다.

입출력 예

n	return
3	2
5	5

입출력 예 설명

피보나치수는 0번째부터 0, 1, 1, 2, 3, 5, ... 와 같이 이어집니다.

---

✍ SOLUTION1

const solution = (n) => {
    let result = 0;
    let f0 = 0
    let f1 = 1;
    
    for(let i = 2; i <= n; i += 1){
        result = (f0 + f1) % 1234567;
        f0 = f1;
        f1 = result;
    }
    return result;
}

/*
처음 작성한 코드이고, +7점이나 맞았다.

1. 변수 초기화: 결과를 저장할 result 변수를 0으로, 첫 번째 피보나치 수 f0를 0으로, 
두 번째 피보나치 수 f1을 1로 초기한다.
2. 반복문 실행: i를 2부터 시작하여 n까지 1씩 증가시키며 반복한다. 
이 반복문은 n이 2 이상일 때, 즉 피보나치 수열에서 세 번째 항 이상을 계산할 때만 실행된다.
3. 피보나치 수 계산: 각 반복에서, result에 f0과 f1을 더한 값의 1234567로 나눈 나머지를 저장한다. 
4. 값 갱신: f0에는 f1의 값을, f1에는 방금 계산한 result의 값을 할당하여, 다음 반복에서 
사용할 피보나치 수열의 항을 준비한다.
5. 결과 반환: 반복문이 끝나면, result에 저장된 값을 반환한다. 
*/

✍ SOLUTION2

const solution = (n) => {
    const memo = [0, 1]; 
    
    for (let i = 2; i <= n; i++) {
        memo[i] = (memo[i - 1] + memo[i - 2]) % 1234567;
    }
    
    return memo[n];
};

/*
SOLUTION1과는 다르게 메모이제이션을 사용하되 for문과 같이 사용하는 방식으로 작성해보았다.
재귀를 사용하지 않은 이유는 아래 쪽에 설명해두겠다.

1. 메모이제이션 배열 초기화: 함수는 memo라는 이름의 배열을 선언하고, memo[0]에는 0을, 
memo[1]에는 1을 할당한다. 이 두 값은 피보나치 수열의 시작 조건, 즉 F(0) = 0, F(1) = 1을 나타낸다.
2. 반복문을 통한 피보나치 수열 계산: 코드는 for 반복문을 사용하여 i가 2에서 시작하여 n까지 1씩 
증가하면서 반복된다. 이는 피보나치 수열에서 세 번째 항(F(2))부터 n번째 항까지 각 항을 계산하기 위함이다.
3. 현재 항의 값 계산 및 저장: 반복문 내에서, memo[i]에는 memo[i - 1]과 memo[i - 2]의 
합을 1234567로 나눈 나머지를 저장한다. 
4. 결과 반환: 마지막으로, 함수는 memo[n]을 반환한다. 이 값은 요청된 n번째 피보나치 수를 
1234567로 나눈 나머지이다.
*/

---

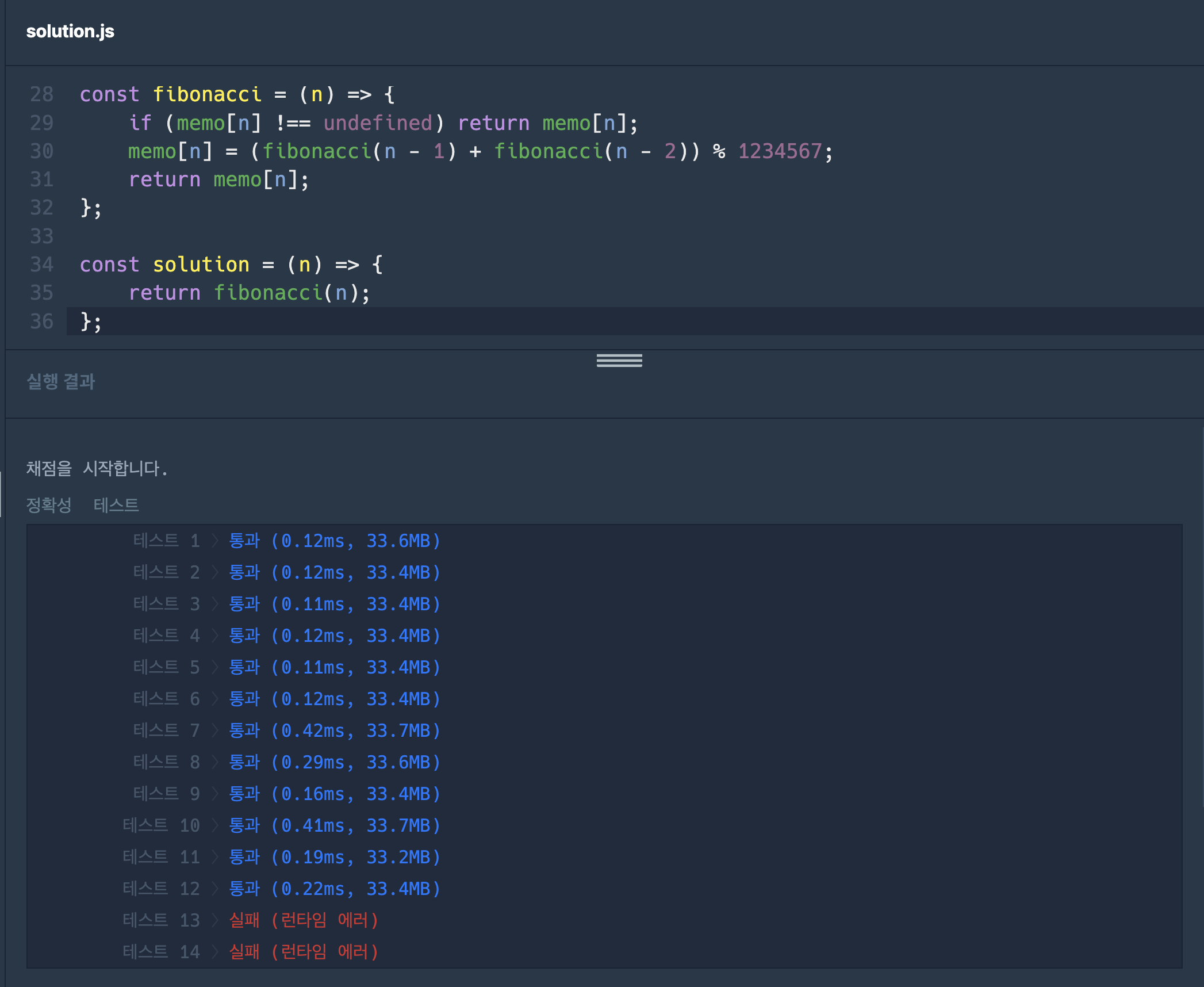
✍ runtime error가 발생했던 코드

const memo = [0, 1];

const fibonacci = (n) => {
    if (memo[n] !== undefined) return memo[n]; 
    memo[n] = (fibonacci(n - 1) + fibonacci(n - 2)) % 1234567;
    return memo[n];
};

const solution = (n) => {
    return fibonacci(n);
};

/*
런타임 에러가 발생했던 이유는 재귀 함수의 호출 깊이가 너무 깊어서 스택 오버플로가 발생해서 그런것 같다.
찾아보니 제시된 문제에서 n은 최대 100,000까지 될 수 있으며, 재귀 호출로 이를 처리하는 것은 
실제 환경에서는 비효율적이거나 불가능할 수 있을 수 있다고 한다. 그래서 SOLUTION2 와 같이 
메모이제이션을 사용하되 재귀가 아닌 반복문으로 풀이하는 방식으로 접근해보았다.

1. 메모이제이션 배열 초기화: 전역 변수 memo를 배열로 선언하고, memo[0]에는 0을, memo[1]에는 1을 
할당하여 초기화한다. F(0) = 0과 F(1) = 1을 설정하는 것이다.
2. 피보나치 함수 정의: fibonacci라는 이름의 함수를 정의한다. 매개변수로 정수 n을 받아, 
피보나치 수열의 n번째 항을 계산한다.
3. 메모이제이션 검사: fibonacci 함수 내에서, 먼저 memo[n]이 undefined가 아닌지 확인한다. 
이는 n번째 피보나치 수가 이미 계산되어 memo 배열에 저장되어 있는지를 검사하는 단계이다. 
만약 memo[n]에 값이 있으면, 즉 undefined가 아니면, 해당 값을 바로 반환한다. 
4. 재귀적 계산 및 저장: memo[n]에 값이 없다면, 즉 n번째 피보나치 수가 아직 계산되지 않았다면, 
fibonacci(n - 1) + fibonacci(n - 2)를 계산한다. 계산된 결과는 1234567로 나눈 나머지를 
memo[n]에 저장하고, 이 값을 반환한다.
5. 솔루션 함수: solution 함수는 단순히 fibonacci 함수에 n을 전달하고, 그 결과를 반환한다.
*/

출처 : 프로그래머스 스쿨 | 코딩테스트 연습