문제 링크

문제 간단 해석

주어진 배열에서 최대 정사각형의 크기를 찾는 문제. DP 형식으로 풀면 빠르고 깔끔하게 풀 수 있다. 정답률은 높지만, Python으로 풀 당시 개인적으로 많이 어려워했다.

Java

풀이 코드

import java.util.Arrays;

class Solution {
    public int solution(int [][]board) {
        int[] checkSize = new int[3];
        int maxSize = 0;

        for (int r = 0; r < board.length; r++) {
            for (int c = 0; c < board[0].length; c++) {
                if (board[r][c] == 0)
                    continue;

                if (r != 0 && c != 0) {
                    checkSize[0] = board[r-1][c-1];
                    checkSize[1] = board[r][c-1];
                    checkSize[2] = board[r-1][c];

                    Arrays.sort(checkSize);
                    board[r][c] = checkSize[0] + 1;
                }

                maxSize = Math.max(board[r][c], maxSize);
            }
        }

        return maxSize * maxSize;
    }
}

해석

for (int r = 0; r < board.length; r++) {
    for (int c = 0; c < board[0].length; c++) {
        if (board[r][c] == 0)
            continue;

        if (r != 0 && c != 0) {
            checkSize[0] = board[r-1][c-1];
            checkSize[1] = board[r][c-1];
            checkSize[2] = board[r-1][c];

            Arrays.sort(checkSize);
            board[r][c] = checkSize[0] + 1;
        }

        maxSize = Math.max(board[r][c], maxSize);
    }
}

return maxSize * maxSize;

이중 for문을 사용하여 주어진 배열 내 값을 하나씩 차례대로 볼 것이다.
만약 해당 값이 0이라면, 건너뛴다.

r과 c가 둘 다 0이 아니라면, 해당 위치의 좌상단, 좌측, 상단의 값을 확인하고 최솟값 + 1을 구해 배열에 넣는다.
그 후 가장 큰 값을 maxSize에 유지하도록 한다.

왜 이런 식이 나왔는지 그림을 그리며 이해해보자.

먼저, 2 * 2 정사각형이 만들어지는 경우를 살펴보자.

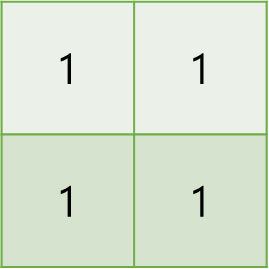
2 * 2 배열 내의 모든 값이 1이므로 2 * 2 정사각형이 만들어진다.
이 때, 우측 하단 값을 기준으로 하면 왼쪽 위, 왼쪽, 위쪽 값이 모두 1이므로 2 * 2 정사각형이 생성된다고 볼 수도 있다.

이번엔 3 * 3 정사각형을 살펴보자.

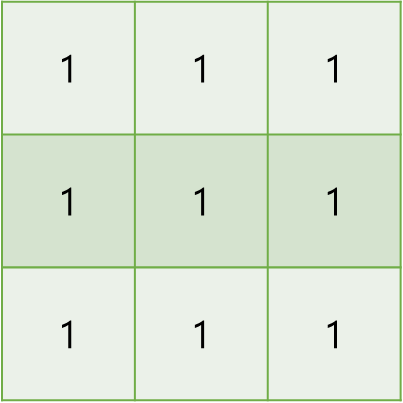
3 * 3 정사각형 내에는 당연히 2 * 2 정사각형을 찾아낼 수 있다. 우측 하단 값을 포함하지 않는 2 * 2 정사각형을 그려보자.

..색 범위가 겹쳐 알아보기 힘드니, 2 * 2가 완성되는 사각형의 우측 하단값을 '2'라고 작성해보자.

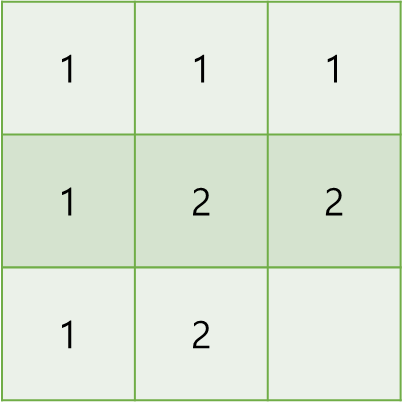
이 때, 3의 완성은 마찬가지로 왼쪽 위, 왼쪽, 위쪽 값이 모두 2이므로 완성된다고 볼 수 있다.

이 개념을 더 확장시켜서 y, x 위치의 값을 확인하는 경우 좌상단측의 3방향을 확인한다고 생각해보자.

초록색의 값을 결정하는 데에는 좌상단측 3방향 사각형의 유효크기를 확인하면 된다. 회색, 파란색, 주황색 값들은 모두 1로 차있으므로 초록색에서 완성되는 정사각형의 크기는 회색, 파란색, 주황색 크기 + 1과 같다.

만약, 중간에 0이 들어가서 특정 사각형의 유효크기가 줄어든다면?

파란색 크기의 + 1 까지는 초록색이 완성될 수 있으나, 그 밖의 범위에는 0이 포함되므로 초록색은 파란색 크기 + 1과 같아진다.

즉, 3방향 사각형의 크기 중 가장 작은 값 + 1과 같아진다고 볼 수 있다.
이 때, 우리는 사각형의 크기를 우하단에 몰아넣기로 했으니 초록색의 크기는 초록색의 좌상단, 좌측, 상단의 값을 확인하고 최솟값을 구한 후 + 1 해준 것과 같다고 보면 된다.

Python

풀이 코드

def solution(board):
    row = len(board)
    col = len(board[0])

    for r in range(1, row):
        for c in range(1, col):
            if board[r][c]:
                board[r][c] = min(board[r - 1][c], board[r][c - 1], board[r - 1][c - 1]) + 1

    answer = 0
    for r in range(row):
        answer = max(*board[r], answer)

    return answer ** 2

해석

Java와 같다.