플로이드 워셜 알고리즘

플로이드 워셜 알고리즘이란?

• 모든 노드에서 다른 모든 노드까지의 최단 경로를 계산

• 다익스트라 알고리즘과 마찬가지로 단계별로 거쳐가는 노드를 기준으로 알고리즘을 수행
  - 매 단계마다 방문하지 않은 노드 중에 최단 거리를 갖는 노드를 찾는 과정이 필요하지 않는다.

• 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장

• 플로이드 워셜 알고리즘은 다이나믹 프로그래밍 유형에 속한다.

• 각 단계마다 특정한 노트 K를 거쳐 가는 경우를 확인한다.
  -A에서 B로 가는 최단 거리보다 A에서 K를 거쳐 가는 거리가 더 짧은지 검사한다

• 점화식은 아래와 같다
  

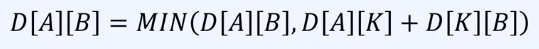
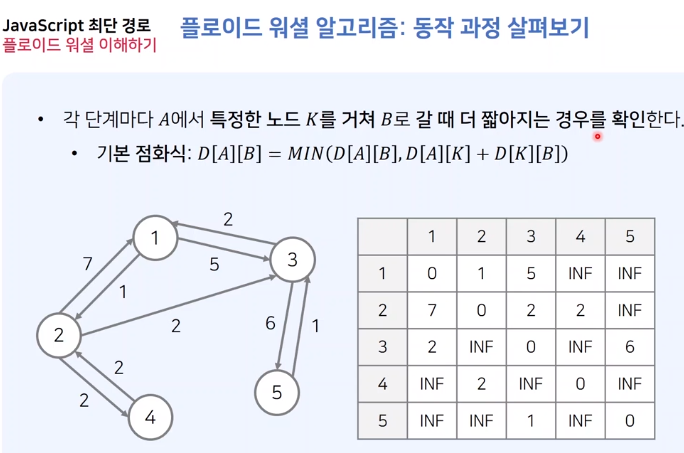
플로이드 워셜 알고리즘 동작 과정

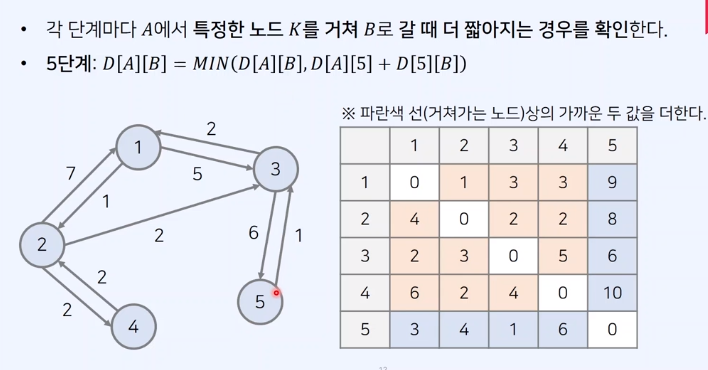
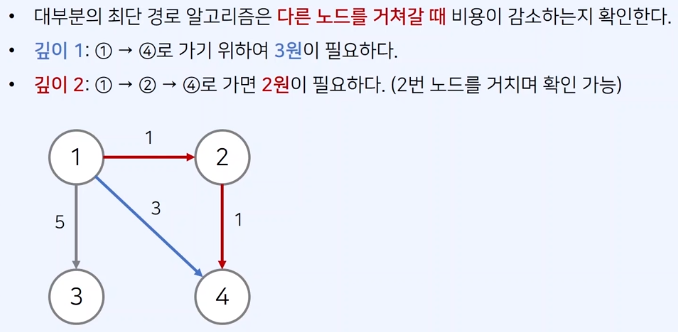
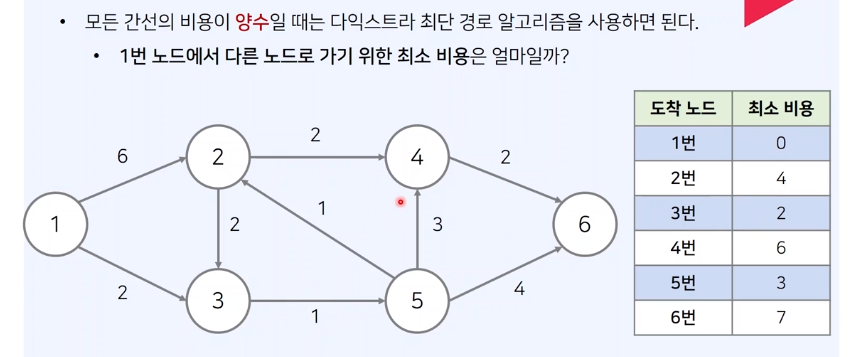
최단 경로 알고리즘의 특징

음수 간선이 포함된 상황에서의 최단 거리 문제

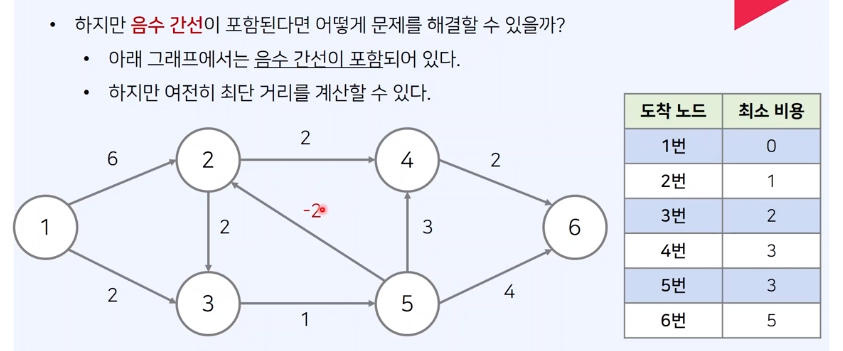
이 경우 최단 거리가 음의 무한인 노드가 발생한다.

벨만 포드 최단 경로 알고리즘

• 음수 간선에 관하여 최단 경로 문제는 다음과 같이 분류할 수 있다.

1. 모든 간선이 양수인 경우
2. 음수 간선이 있는 경우
   • 음수 순환이 없는 경우
   • 음수 순환이 있는 경우

• 벨만 포드 최단 경로 알고리즘은 음의 간선이 포함된 상황에서도 사용할 수 있다.
• 또한 음수 순환을 감지할 수 있다.
• 벨만 포드의 기본 시간 복잡도는 O(VE)로 다익스트라 알고리즘에 비해 느리다.
  - 기본적으로 동작 과정에서 다익스트라 알고리즘의 최적의 해를 항상 포함한다.
  

1. 출발 경로를 설정
2. 최단 거리 테이블을 초기화
3. 다음의 과정을 N -1 번 반복
   1. 전체 간선 E개를 하나씩 확인
   2. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신

• 만약 음수 순환이 발생하는지 체크하고 싶다면 3번의 과정을 한 번 더 수행
  - 이때 최단 거리 테이블이 갱신 된다면 음수 순환이 존재하는 것

벨만포드 vs 다익스트라

• 다익스트라
  - 매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택
  • 음수 간선이 없다면 최적의 해를 찾을 수 있다.
• 벨만포드
  - 모든 간선을 매번 전부 확인
  ->따라서 다익스트라 알고리즘에서의 최적의 해를 항상 포함
  • 다익스트라 알고리즘에 비해 시간이 오래 걸리지만 음수 순환을 탐지 가능