다이나믹 프로그래밍

다이나믹 프로그래밍이란?

• 통상적으로 메모리를 더 사용하여 시간 복잡도를 개선할 때 많이 사용된다.
• 구체적으로, 시간 복잡도가 비효율적인 알고리즘이 있을 때 부분 문제의 반복이 발생하는 경우 적용하면 효과적이다.
• 다이나믹 프로그래밍 문제를 해결하기 위한 점화식을 찾는 것이 핵심 과정이다.

다이나믹 프로그래밍 사용 조건

다이나믹 프로그래밍은 일반적으로 아래 두 조건을 만족할 때 사용할 수 있다.
1. 최적 부분 구조 (optimal substructure)

• 큰 문제를 유사한 형태의 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아 큰 문제를 해결

2. 반복되는 부분 문제 (overlapping sub-problem)

• 동일한 작은 문제를 반복적으로 해결해야 한다.

점화식과 최적 부분 구조

• 점화식 : 인접한 항으로 현재 값을 결정하는 관계식을 의미
  - 일반적으로 최적 부분 구조를 만족한다는 특징이 있다.
  

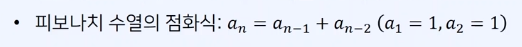
점화식의 구성 요소

• 초기항
• 인접한 항과의 관계
• 점화식은 재귀함수로 표현할 수 있다.
• 재귀 함수는 종료 조건이 있어야 하는데, 이것이 점화식의 초기항과 같은 역할을 수행한다.

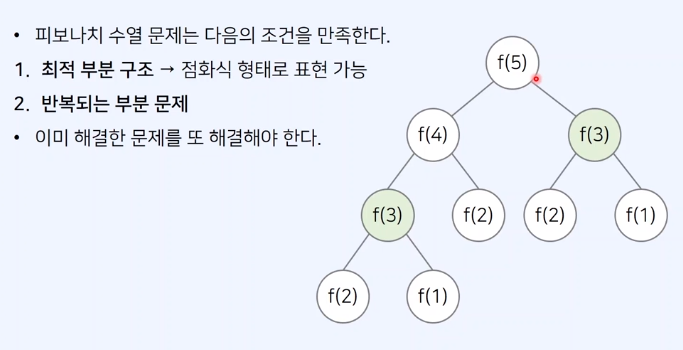
피보나치 수열 문제

다이나믹 프로그래밍의 일반 형태

• 피보나치 수열의 점화식을 그대로 재귀 함수로 구현하면 중복되는 문제가 발생한다. (이미 구한 값을 불필요하게 반복 계산)

• 다이나믹 프로그래밍은 이 문제를 해결할 수 있도록 해준다.

다이나믹 프로그래밍 문제 해결 과정

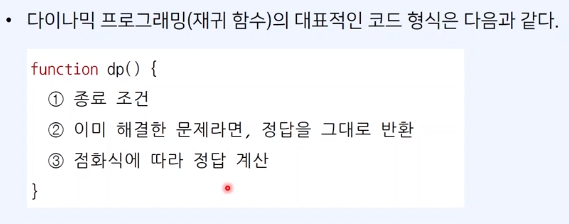
1. 문제 이해하기
   2. 점화식 찾아내기
2. 구현방식 (상향식/하향식) 결정하기
3. 점화식을 실제 코드로 구현하기

다이나믹 프로그래밍 문제 접근 방법

1. 상향식 : 반복문을 이용해 초기 항부터 계산한다.
2. 하향식 : 재귀 함수로 큰 항을 구하기 위해 작은(이전) 항을 호출하는 방식이다.
   이미 구한 함수를 담는 테이블을 흔히 dp테이블이라고 한다.

• 하향식

• 상향식