[Information Security] Chapter 21. Public-Key Cryptography and Message Authentication

4학년 1학기, Information Security 수업을 듣고, 해시/공개키 암호화에 대해 정리한 내용이다.

Simple Hash Functions

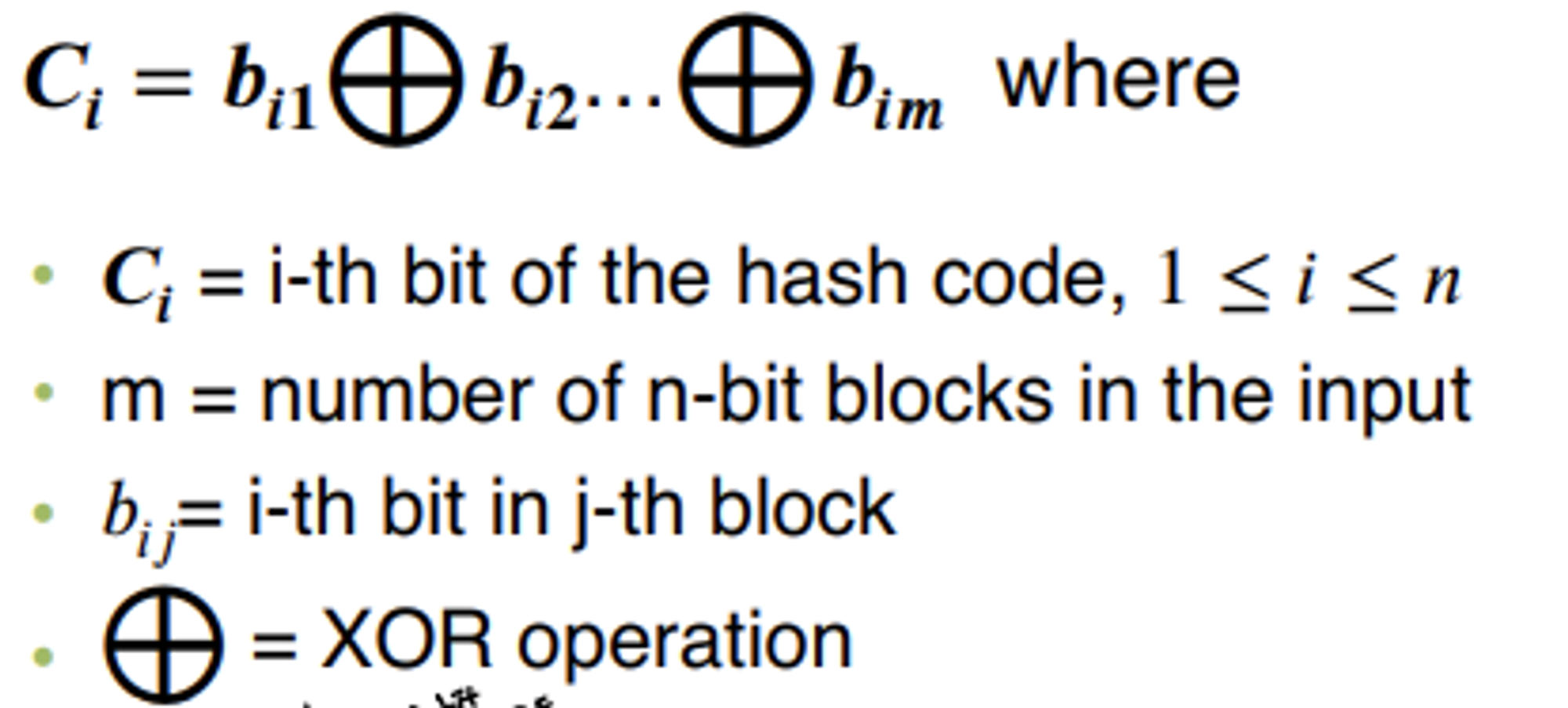
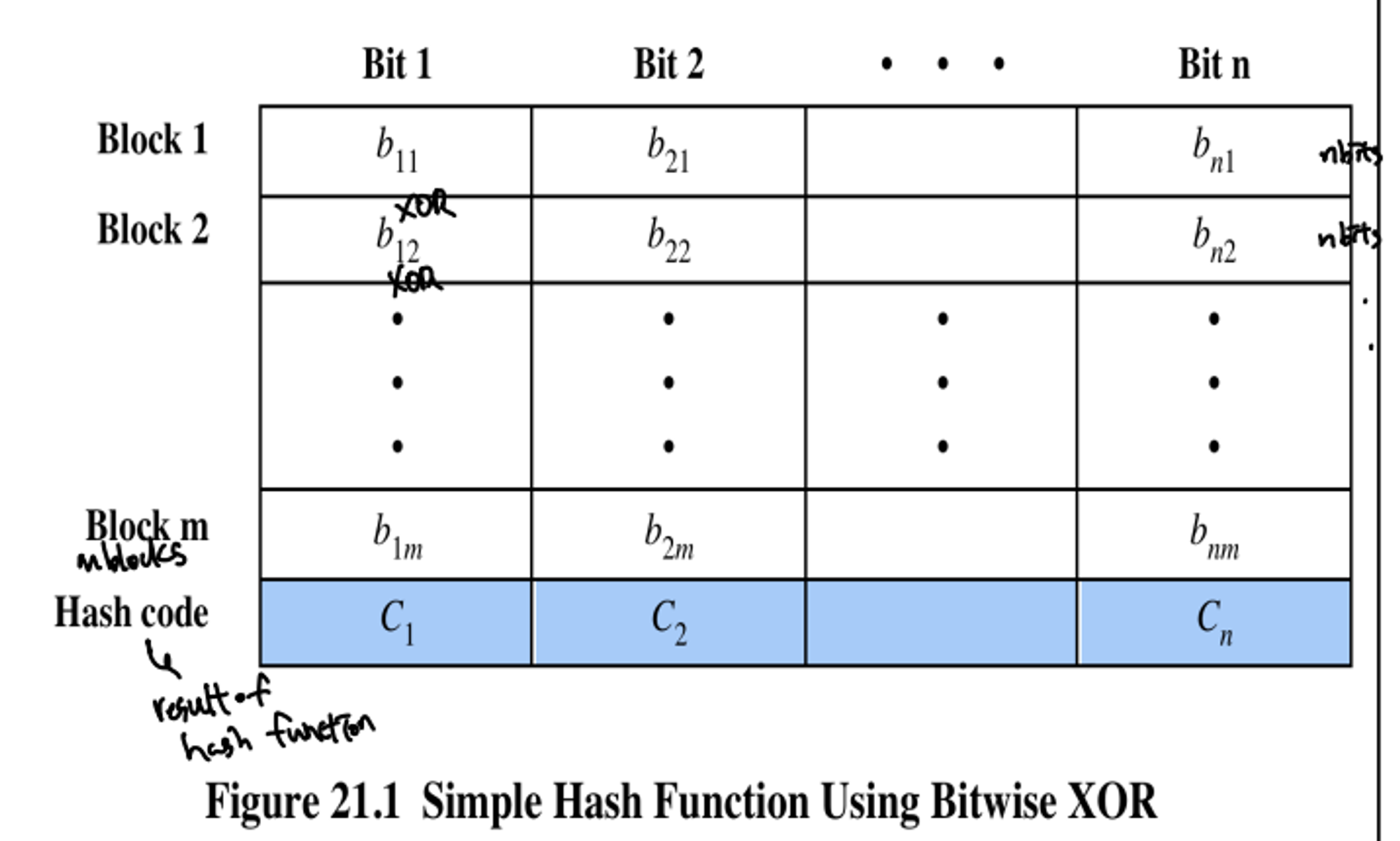
Simple Hash Function Using Bitwise XOR

• bit-by-bit XOR of every block
  • 입력 메세지의 총 크기는 n*m bit → 입력 메시지를 n-bit 크기의 블록으로 나눔. 따라서 전체 메시지는 m개의 n-bit 블록으로 구성됨
  • 각 블록에서 동일한 위치에 있는 비트들끼리 XOR연산을 수행
  • 이렇게 하여, 각 비트 위치에서 모든 블록의 비트들을 XOR 연산한 결과를 얻게 됨 → 원래 메시지의 해시코드(n-bit)

• efficiency? security?
  • XOR 연산은 매우 빠르기 때문에 hash function은 암호화가 매우 빠름
  • 그러나 많은 조합들로 같은 hash code를 만들 수 있기 때문에 그렇게 secure하지 않다. ex) H(’abc’)=H(’aTH’)

얘를 좀 더 secure 하게 만들기 위해 고안된 것

Improvement of bit-by-bit XOR approach

• 달라진 것: At the end of every block processing, the hash value is shifted by 1-bit
• 예시: Hash of “test” with 8-bit block
• 그럼 이 방법은 안전한 해시 함수일까?
  • Collision resistance 관점
    • 해시 값에 대한 1비트 시프트는 easy function으로 충분한 혼돈성을 제공하지 못하며, XOR 연산은 단순하므로, 원본 메시지의 길이가 짧거나 패턴이 반복될 경우, 다른 입력값을 찾아 동일한 해시를 생성할 수 있음

A variant of hash code for message authentication

1. XORing all message blocks of 64-bit each Xi(i-th message block)

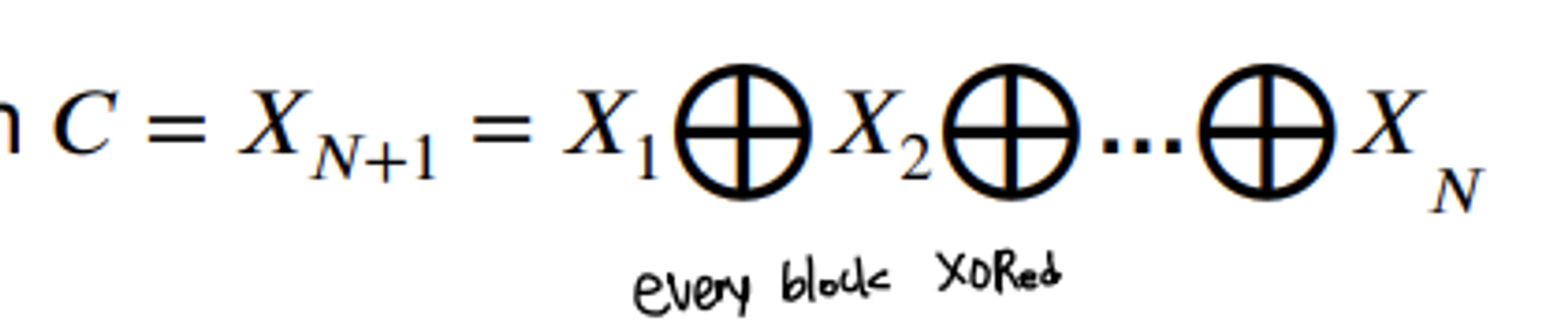
2. Encrypt all the blocks except the hash code using ECB mode

• Yi = E(Xi)

3. 각각의 Yi를 decryption 하여 Xi를 얻어내고, XOR 연산을 통해 C와 같으면 message는 verified

• Problem?
  • Although without key, hacker cannot make encryption, but this method has weakness, hacker can change order of Xi
  • 순서를 바꿔도 XOR 수행 결과는 같으므로 hash code가 같아질 것임

Simple Hash function을 해결하기 위해 나온 것이 SHA

Secure Hash Algorithm(SHA)

• developed by NIST, published in 1993
• 1995년: SHA-1, 2002년: SHA-256, SHA-384, SHA-512 (Same basic structure as SHA-1 but greater security)

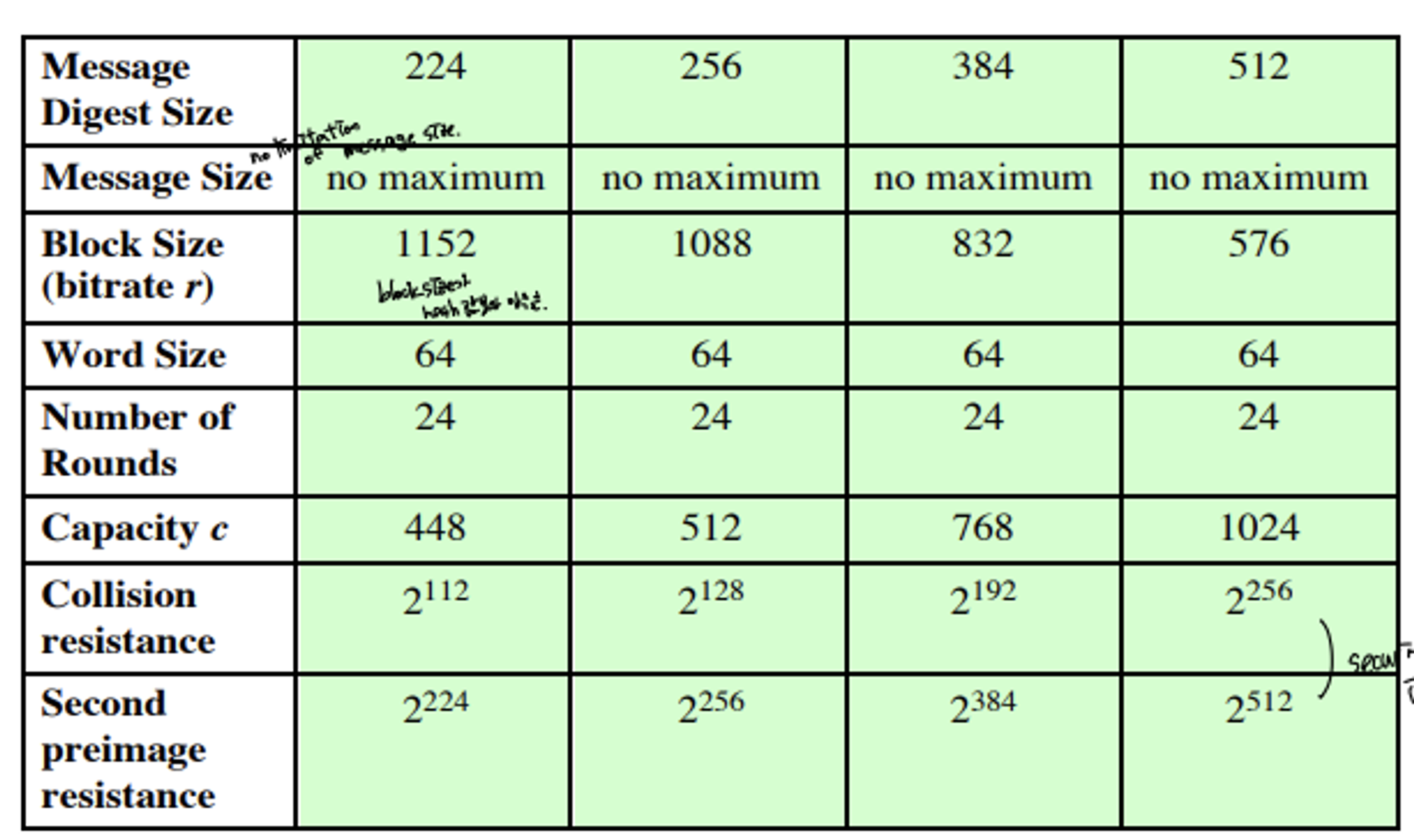
Comparision of SHA Parameters

• All sizes are measured in bits

	SHA-1	SHA-256	SHA-384	SHA-512
Message digest size(Hash value size)	160	256	384	512
Message size	<2^64	<2^64	<2^128	<2^128
Block size	512	512	1024	1024
Word size	32	32	64	64
Number of steps	80	64	80	80
Security	80	128	192	256

• Security refers to the fact that a birthday attack on a message digest of size n produces a collision with a work factor of approximately 2^(n/2)
  • message digest 값 크기가 n이면, birthday attack으로 collision을 찾는데 필요한 작업량은 약 2^(n/2)

Message Digest Generation Using SHA-512a(SHA2)

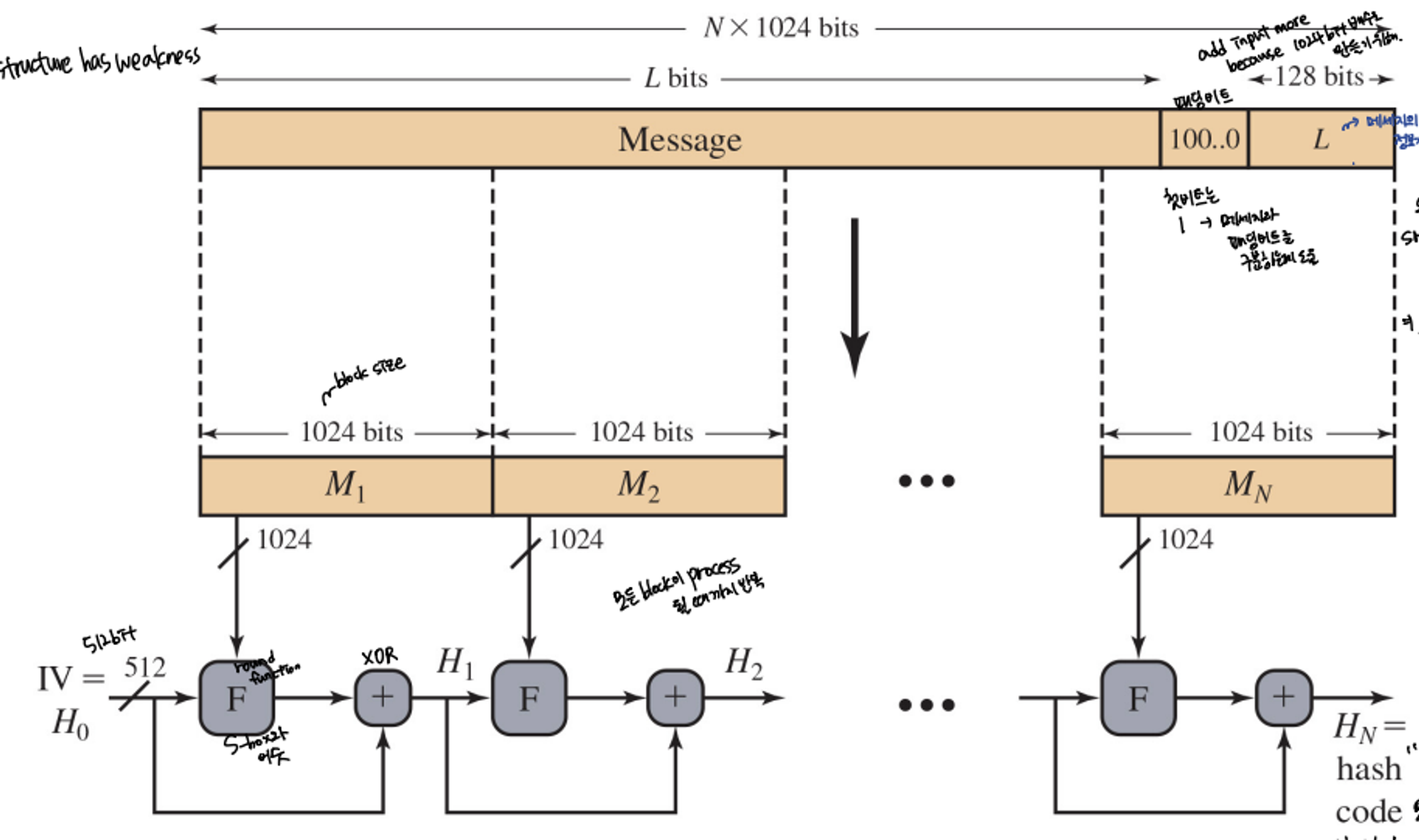
1. Add padding bit and 128-bit of L with message’s length information
   • The first bit of padding bit is 1 and the others are 0 to distinguish original message
   • L이 128-bit인 이유: SHA-512는 Message size <2^128이므로 최대 2^128-1 길이 정보까지 저장이 가능해야 함
2. The input(Message+ padding bit+ L) is divided into 1024 bits of blocks
3. Each message block(Mi) performs round funciton F with Hi-1 to make Hi

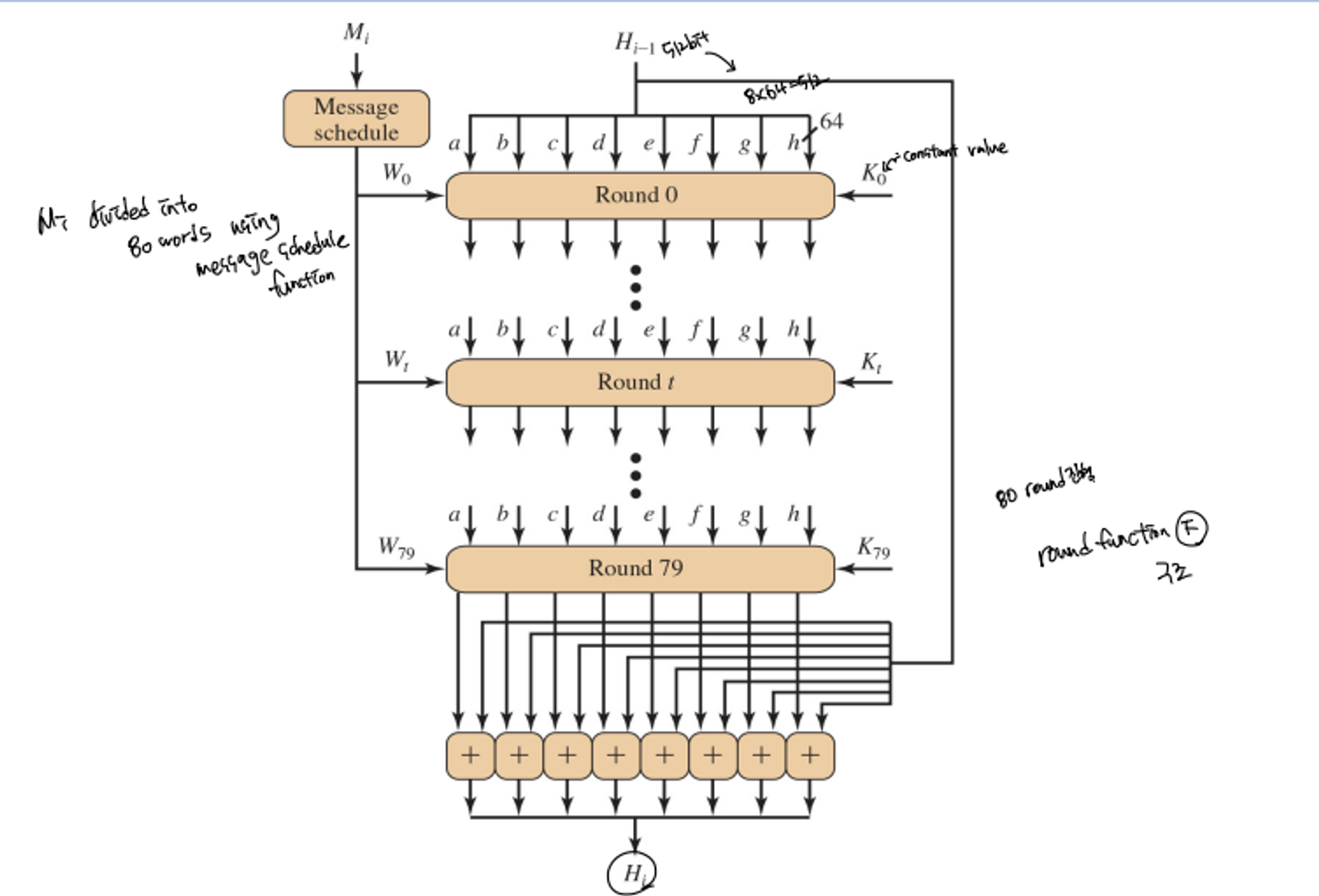
• Ho = IV
• 80 rounds are performed
  a. Mi(1024=16*64) is divided into 80 words(64bit) by using message schedule function
  - Mi를 80words로 어떻게 확장하나?
  - 먼저 16개의 Wo~W15를 구성하고, 이후 shift, rotate bit, xor operation을 이용하여 새로운 words를 생성하여 확장
  

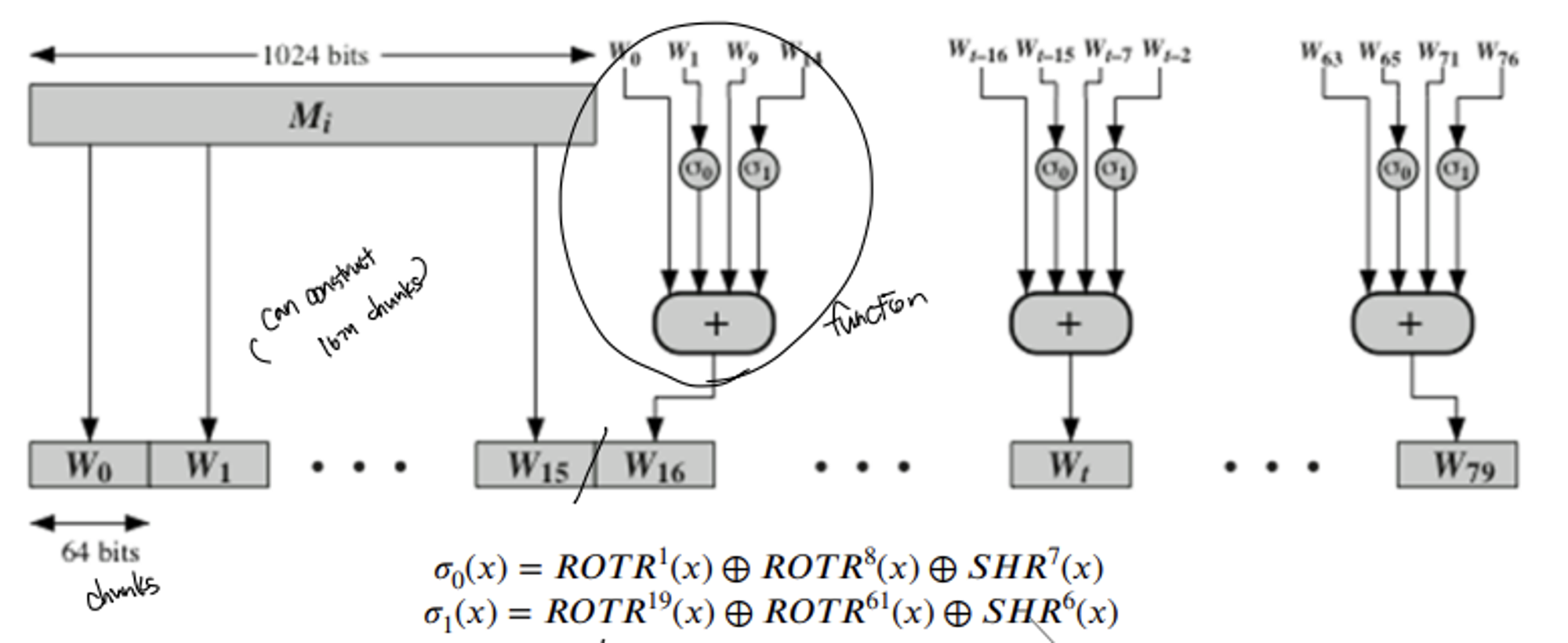
b. Initiate a~h(each is 64-bit) from Hi-1
c. Process each round function by using Wi, Ki(cotant value), a~h, after that each a~h is updated by bit rotate, shift, logic operation
d. Generate Hi by XOR operation between Hi-1 and updated a~h after round 79

4. After all message blocks is processed, hash code Hn is generated

• it means all state effects ouput → weakness
• When attacker knows Hn, attacher can attached other message to original message, then attacker can make new H’

SHA-3

SHA-3 is a cryptographic hash function that is intended to complement SHA-2 as the approved standard for a wide range of applications

Requirements

• Must support has value lengths of 224,256,384, and 512 bits
• Algorithm must process small blocks at a time instead of requiring the entire message to be buffered in memory before processing it
  • 메시지를 작은 블록으로 나누어 순차적으로 처리하며, 모든 메시지를 한 번에 메모리에 버퍼링할 필요 없이 메모리 사용량을 줄이고, 메시지의 길이에 관계없이 일정한 메모리만을 사용해 처리할 수 있게 해줌

SHA-3 syntax

• NIST chose the Keccak as the new SHA-3 standard

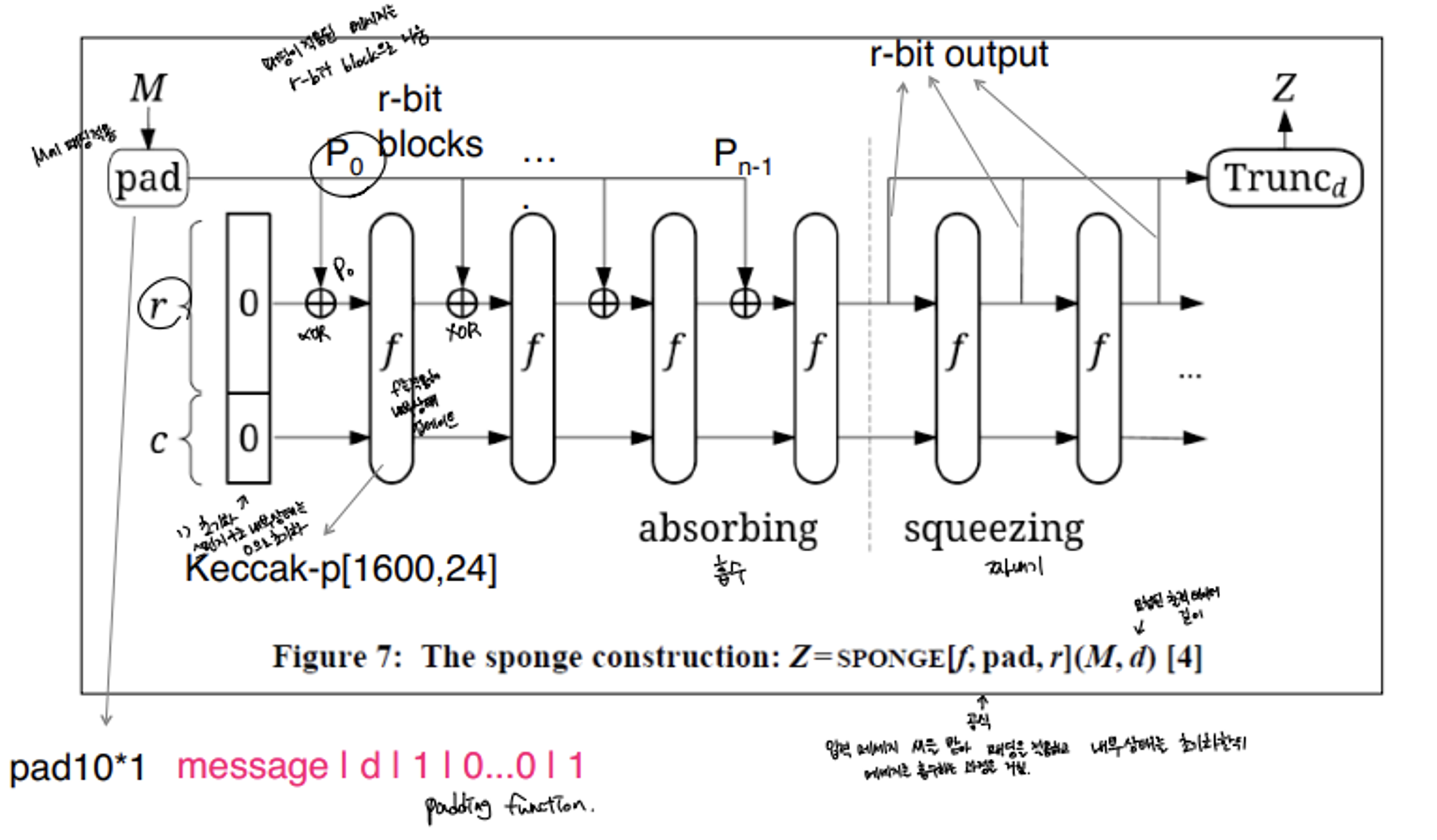
The Sponge Construction: Basic structure of SHA-3

• Takes an input message and partitions it into fixed-size blocks
• Each block is processed in turn with the output of each iteration fed into next iteration, finally producing an output block
• Input
  

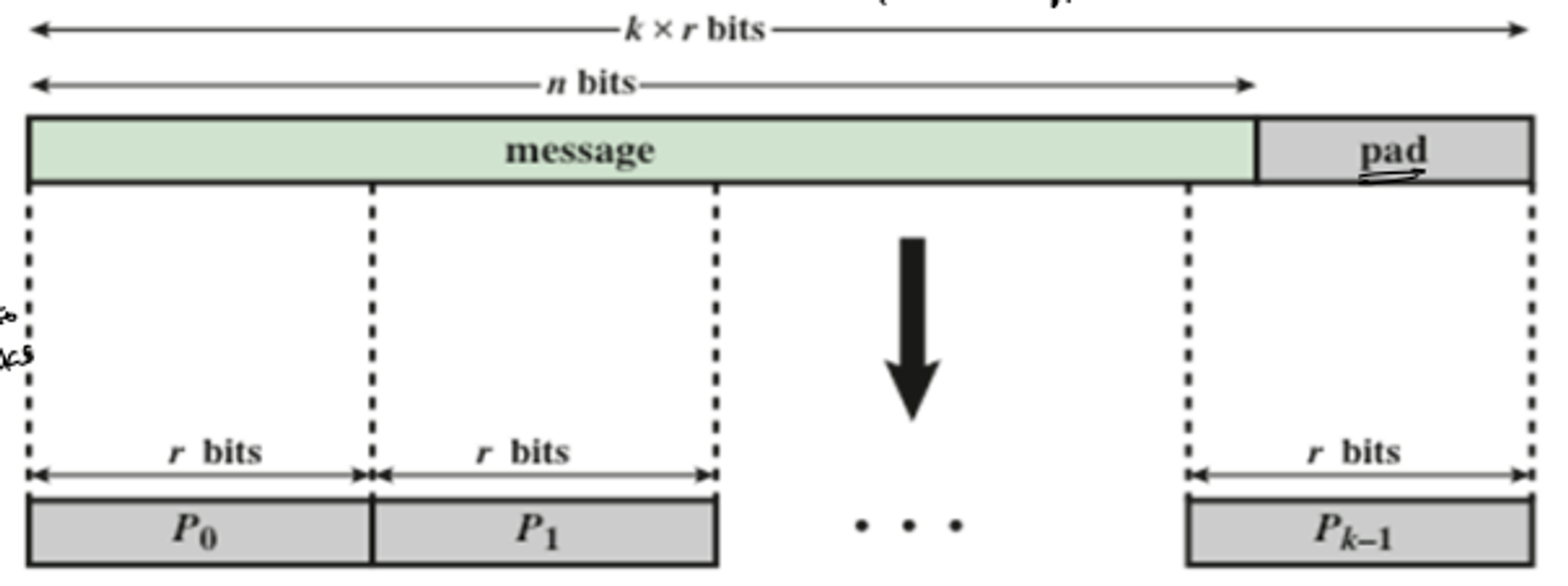
- Makes message multiple of r-bits by using pad(the padding algorithm)
- padding bit: first bit and last bit should be 1 and the other bits should be 0

• Output
  

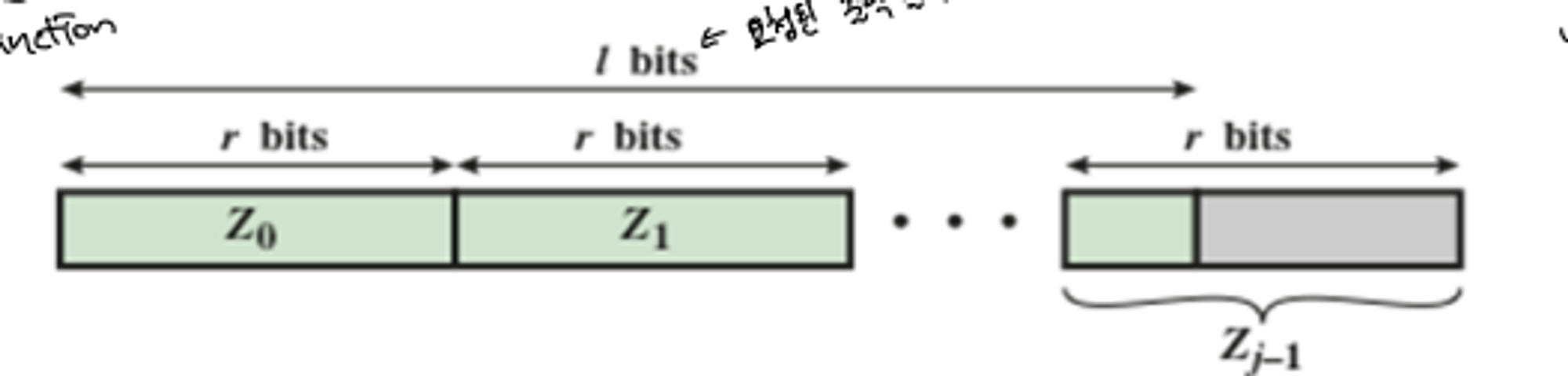
- l bits which is requested as output bit’s length

• SPONGE construnction
  • Message which is applied padding function is divided into r-bits blocks(Pi)
  • Absorbing
    • Initiate State Matrix which consists of r, c with 0
      • State Matrix는 초기에 모두 0으로 설정됨. 크기는 고정되어 있으며, 데이터는 여기에 흡수됨
      • r은 외부에서 입력되는 데이터 또는 출력으로 나가는 데이터가 저장되는 부분
      • c는 상태 행렬의 보안수준을 정의. 직접적으로 메시지 데이터를 저장, 출력하진 않음
    • State matrix is updated by XOR operation with Pi
    • Iteration Function f changes state matrix by using multiple operation
  • Squeezing
    • State matrix에서 r-bit 부분만이 output으로 추출됨
    • 최종 해시 값이 요청된 출력 길이보다 길 경우, Trunc 작업을 통해 원하는 길이로 조정됨
    • 최종적으로 출력 Z를 생성

HMAC

키를 활용한 인증방식으로 메시지 무결성을 보호하는데 사용됨. 해시 함수 H, 비밀 키 K를 사용하여 메시지 M의 인증 코드를 생성하는 방식

• Interest in developing a MAC derived from a cryptographic hash code
  • Why?
  • Cryptographic hash functions generally execute faster
  • Libray code is widely available
  • SHA-1 was not designed for use as a MAC because it does not rely on a secret key → need new design
• Has been chosen as the mandatory-to-implement MAC for IP security

HMAC Design Objectives

• To use, without modifications, available hash functions
• To preserve the original performance of the hash function without incurring a significant degradation
• To allow for easy replaceability of the embedded hash function in case faster or more secure hash functions are founded or required
• To use and handle keys in a simple way
• To have a well-understood cryptographic analysis of the strength of the authentication mechanism based on reasonable assumptions on the embedded hash function

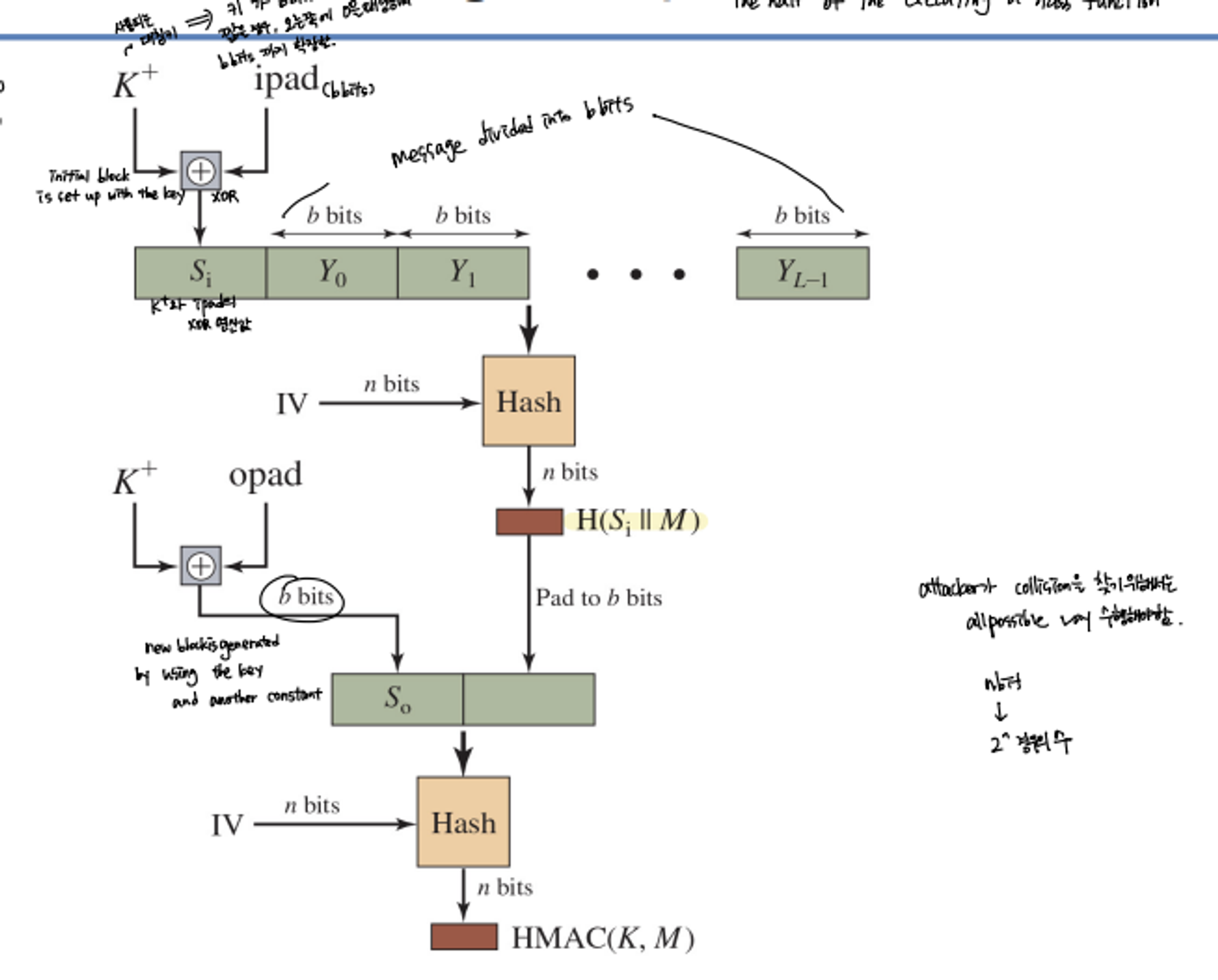
HMAC Structure

• Two hash function are used so which means that the performane is normally the half of the executing a hash funtion

1. 사용되는 대칭 키 K가 b-bits보다 짧은 경우 오른쪽에 0을 붙여 b-bits까지 확장하여 K+ 생성
2. K+(b-bit)와 ipad(b-bit) XOR 연산을 통한 Si 생성하여 b-bits blocks로 나누어진 메시지에 attached
3. H(Si||M) 수행 → b-bit 해시 값 생성
4. New block So is generated by using the K+ and another constant opad(XOR operation)
5. So+H(Si||M) 값은 Hash 함수의 입력값이 되고, 최종 HMAC 코드가 생성됨

Security of HMAC

• Security depends on the cryptographic strength of the underlying hash function
• the probability of successful attack on HMAC is equivalent to one of the following attacks on the embedded hash function
  • Either attacker computes output even with random secret IV
    • Brute force key O(2n), or use birthday attack
  • Or attacker finds collisions in hash function even when IV is random and secret
    • find M and M’ such that H(M)=H(M’)
    • Birthday attack O(2^(n/2))

RSA Public-Key Encryption

• By Rivest, Shamir & Adleman of MIT in 1977
• Best known and widely used public-key algorithm
• Uses exponentiation of integers modulo a prime
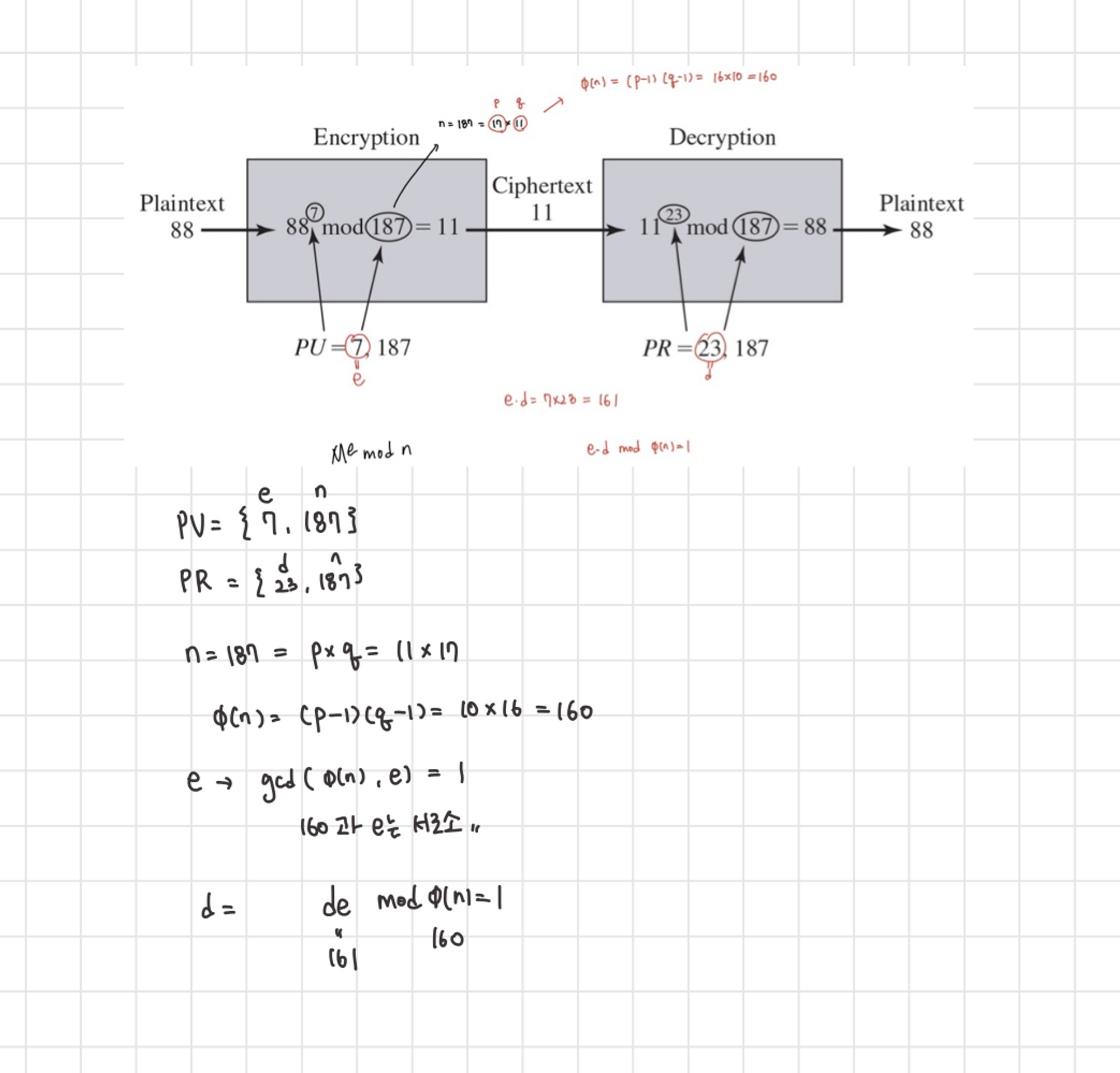
  • Encrypt: C=M^e mod n
  • Decrypt: M = C^d mod n = *(M^e)^d mod n = M
• Public-key encryption PU={e,n} PR= {d,n}
  • Both sender and receiver know values of n and e(공개키)
  • Only recevier knows value of d

The RSA Algorithm

1. Key Generation
   1. Select p, q → p와 q는 서로 다른 소수
   2. Calculate n = p x q → n은 p와 q의 곱
   3. 오일러의 피 함수 계산 = (p-1) x (q-1)
   4. Select integer e → 오일러의 피 함수 값과 e의 최대 공약수는 1이어야 함 (서로소)
   5. Calculate d → de를 오일러의 피 함수값으로 나눈 나머지는 1
   • PU = {e, n}
   • PR = {d, n}

2. Encryption

• Plaintext: M < n
• Ciphertext: C = M^e (mod n)

3. Decryption

• Ciphertext: C
• Plaintext: M = C^d (mod n)

Example of RSA Algorithm

RSA 공격 종류

1. Brute force

• Involves trying all possible private keys

2. Mathematical attacks

• There are several approaches, all equivalent in effort to factoring the product of two primes
  • RSA 암호체계를 공격하는 여러 접근법들이 있으며, 이들은 모두 두 소수의 곱(즉, RSA 공개키의 일부인 n)을 인수분해하는 것과 같은 노력을 필요로 함

3. Timing attacks

• These depend on the running time of the decryption algorithm

4. Chosen ciphertext attacks

• This type of attack exploits properties of the RSA algorithm

Timing Attacks

• Paul Kocher에 의해 널리 알려졌으며, 컴퓨터가 메시지를 복호화하는 데 걸리는 시간을 추적함으로써 공격자가 개인 키를 파악할 수 있음을 보여줌
• 타이밍 공격의 특징
  • Applicable not just to RSA but also to other public-key cryptography system
  • It comes from a completely unexpected direction: 대부분의 암호 분석 기법이 암호 알고리즘의 수학적 취약점을 찾는 반면, 타이밍 공격은 암호화 구현의 물리적 측면, 즉 시간을 이
  • It is a ciphertext-only attack: 공격자가 암호문만 가지고 있어도 공격이 가능함
• 타이밍 공격에 대한 대응(Countermeasures)
  • Constant exponentiation time(고정 시간 연산)
    • Ensure that all exponentiations take the same amount of time before returning a result
  • Random delay
    • Better performance could be achieved by adding a random delay to the exponentiation algorithm to confuse the timing attack
  • Blinding
    • Multiply the ciphertext by a random number before performing exponentiation
    • 2 to 10% performance penalty for blinding

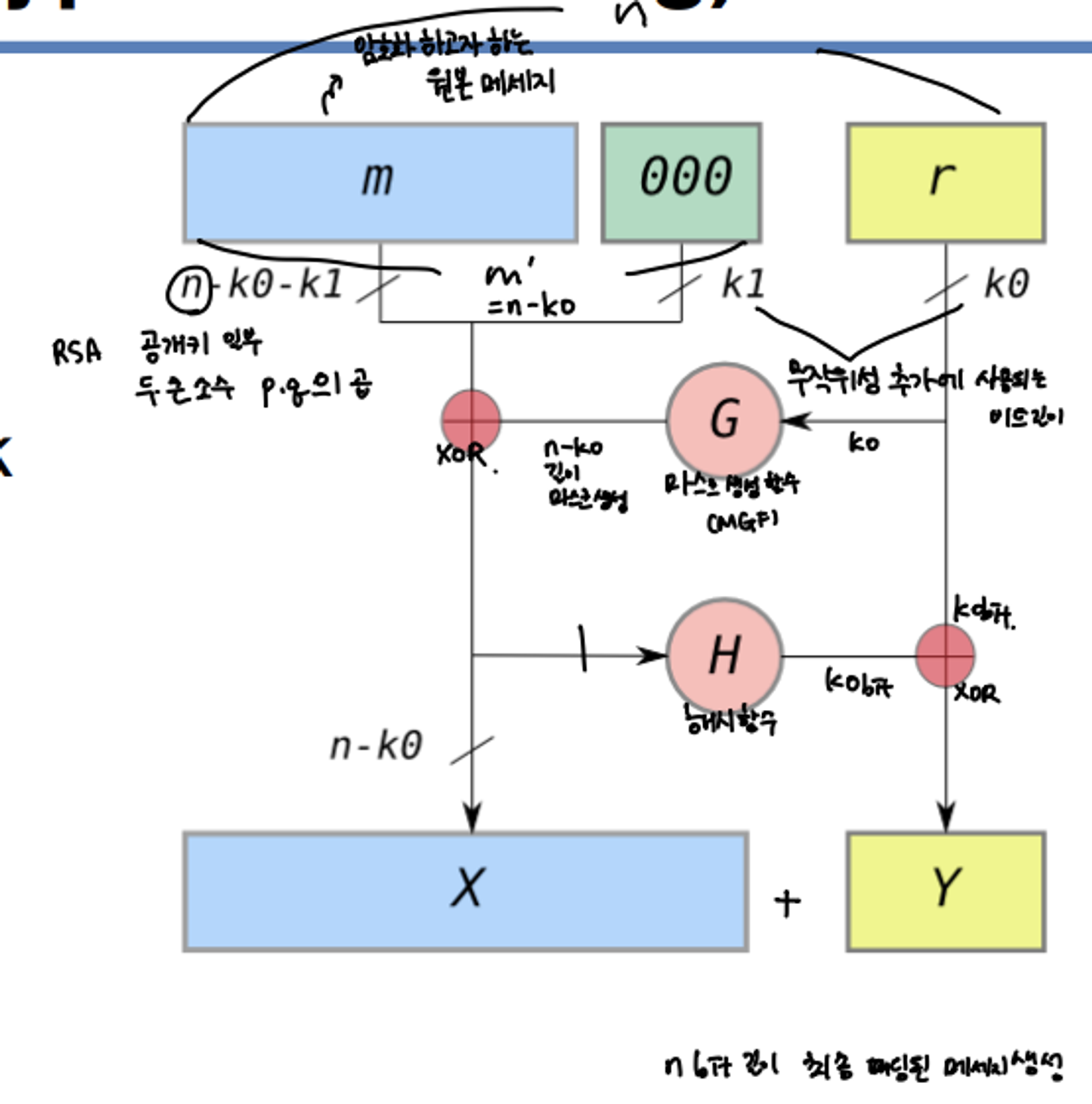
RSA-OAEP(Optimal Asymmetric Encryption Padding)

• RSA 암호화 체계에서 사용하는 패딩 기법 중 하나
• A form of Feistel Network
  • Using a pair of random oracles G, H
  • Proven secure against Chosen Ciphertext Attack

Diffie-Hellman Key Exchange

• First published public-key algorithm
• By Diffie and Hellman in 1976 along with the exposition of public key concepts
• Used in a number of commercial products
• Practical method to exchange a secret key securely that can then be used for subsequent encryption of messages
• Security relies on difficulty of computing discrete logarithms

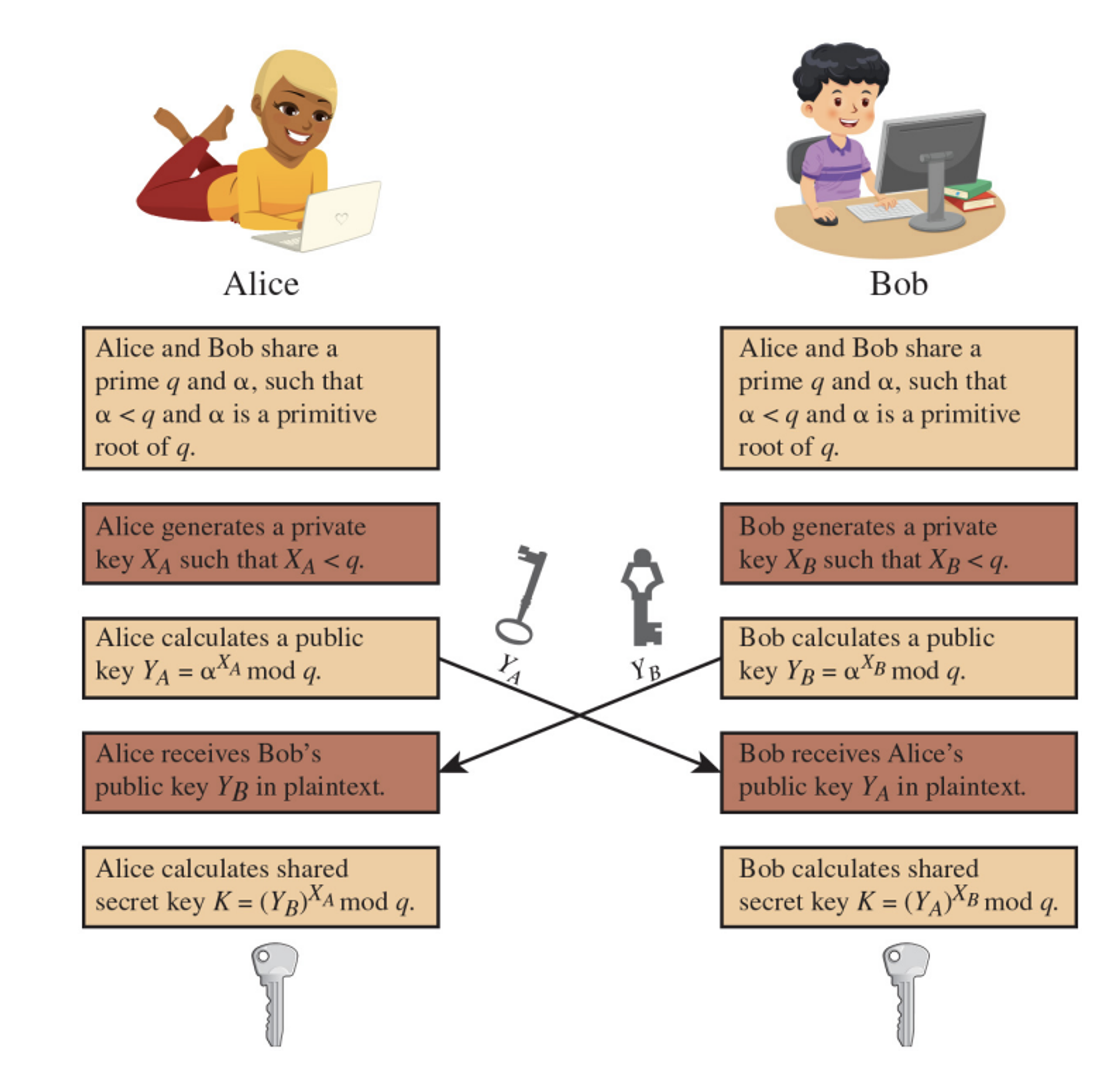
The Diffie-Hellman Key Exchange Algorithm

1. Global Public elements q, 알파 선택 → q는 큰 소수, 알파는 q의 원시근
2. User A 키 생성

• 비밀키 선택
• 비밀키를 이용해 자신의 공개키 계산 → 알파^비밀키를 q로 나눈 나머지

3. User B 키 생성

• 비밀키 선택
• 비밀키를 이용해 자신의 공개키 계산

4. 서로의 공개키 공유
5. 서로의 공유 비밀키 계산

• User A: K = (B의 공개키)^(A의 비밀키)를 q로 나눈 나머지
• User B: K = (A의 공개키)^(B의 비밀키)를 q로 나눈 나머지

Limits of Diffie-Hellman Algorithm: Man-in-the Middle Attack(중간자 공격)

• 악의적인 제 3자가 통신 과정 중간에 끼어들어 각 당사자가 서로 통신하는 것처럼 가장할 수 있음
• 서로가 공개키 Y를 교환하는 과정에서 해커가 끼어들어 수정된 Y를 서로에게 보내는 공격

Other Public-Key Algorithms

Digital Signature Standard(DSS)

• Makes use of SHA-1 and the Digital Signature Algorithm
• Cannot be used for encryption or key exchange
• Only provide the digital signature function

Elliptic-Curve Cryptography(ECC)

• Equal security for smaller bit size than RSA
• Confidence level in ECC is not yet as high as that in RSA

Post-quantum cryptography

• for quantum computer
• NIST started a project to identify and standardize algorithms that resist future cyberattacks

Digital Signature

Properties

• It must verify the author and the date and time of the signature
• It must authenticate the contents at the time of the signature
• It must be verifiable by third parties, to resolve disputes

Requirements

• must be a bit-pattern
• use some information unique to the sender to prevent both forgery and denial
• must be easy
  • to produce the digital signature
  • to recognize and verify the digital signature
• computationally infeasible to forge a digital signature

Basic RSA Signature

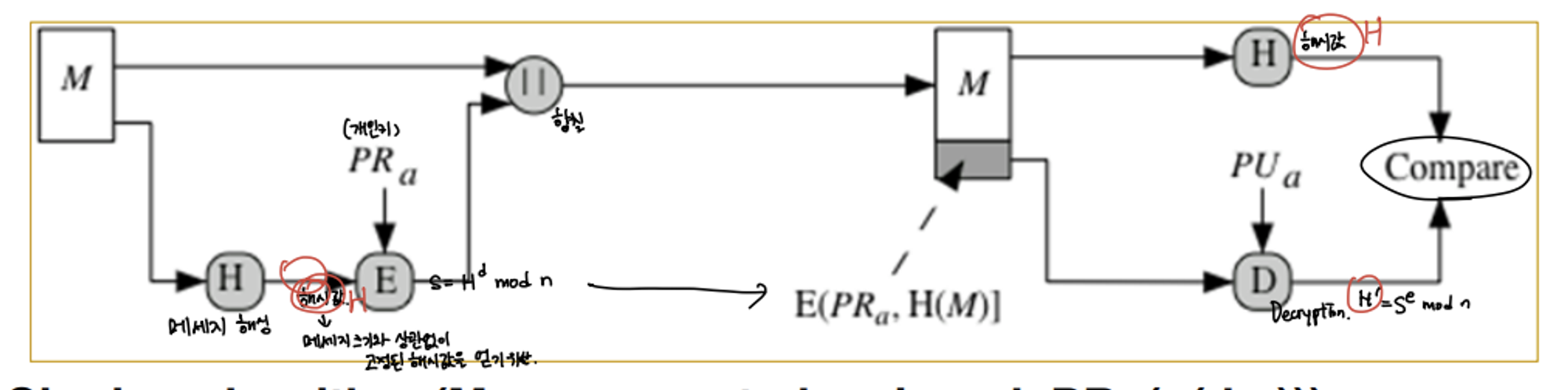
• Problem?
  • 특정 메시지와 서명자(즉, 발신자의 개인키)가 고정되어 있을 때, 그 메시지에 대한 서명이 항상 동일
• Solution? → RSA PSS

RSA PSS

• RSA Probabilistic Signature Scheme
• RSA PSS의 보안성은 기본적으로 RSA 알고리즘의 보안성에 근거함
• Mask Generation Function (MGF)
  • 암호화 해시 함수(예: SHA-3)를 기반으로 하는 메커니즘
  • 기본적인 암호화 해시 함수가 고정된 길이의 출력을 생성하는 것을 바탕으로 하여 가변 길이의 메시지 다이제스트나 해시를 생성하기 위한 암호학적으로 안전한 방법