섹션3, 머신러닝의 기초 이론들

이도현·2023년 9월 11일
0

TensforFlow 2.0으로 배우는 딥러닝 입분(인강)

목록 보기
3/7

1. 머신러닝의 기본 프로세스

1) 가설 정의, 모델정의

  • 선형 회귀 모델: 선형 함수를 이용해서 회귀를 수행하는 기법
  • 선형 회귀 함수는 학습하고자 하는 가설 Hypothesis h(0)을 아래와 같은 선형함수 형태로 표현
y=Wx+by= Wx + b
  • 이때 x와 y는 데이터로 부터 주어지는 인풋 데이터, 타겟데이터이고, W와 b는 파라미터Parameter 0라고 부르며 트레이닝 데이터로부터 학습을 통해 적절한 값을 찾아내야만 하는 값

2) 손실 함수 정의

  • 적절한 파라미터 값을 알아내기 위해서는 현재 파라미터 값이 우리가 풀고자 하는 목적Task에 적합한 값인지 측정할 수 있어야 합니다. 이를 위해 손실함수 Loss Function J(0)을 정의
  • 손실 함수는 여러가지 형태로 정의될 수 있습니다 그 중 가장 대표적인 손실 함수 중 하나는 평균제곱오차 Mean of Squred Error(MSE)입니다.
MSE=1/2n∑i=1nyi..−yiMSE = 1/2n\sum_{i=1}^{n}{y_{i}^{..} - y_{i}}

3) 최적화 정의 - Gradient Descent, 옵티마이저 정의

  • 손실 함수를 최소화 하는 방향으로 파라미터들을 업데이터할 수 있는 학습 알고리즘을 설계해야함
  • 머신러닝 모델은 보통 맨 처음에 랜덤한 값으로 파라미터를 초기화한 후에 파라미터를 적절한 값으로 계속해서 업데이트합니다.
  • 이때, 파라미터를 적절한 값으로 업데이트하는 알고리즘을 최적화Optimization기법이라고 합니다. 여러 최적화 기법 중에서 대표적인 기법은 경사하강법Gradient Descent입니다.
  • 경사하강법: 현재 스텝의 파라미터에서 손실함수의 미분값에 러닝레이터 a를 곱한만큼을 빼서 다음 스텝의 파라미터 값으로 지정합니다.
  • 따라서 손실 함수의 미분값이 크면 하나의 스텝에서 파라미터가 많이 업데이트되고 손실 함수의 미분값이 작으면 적게 업데이트될 것입니다. 또한 러닝레이터 a가 크면 많이 업데이트 a가 작으면 적게 업데이트 될 것입니다.
  • 러닝레이터 알파는 사람이 지정해야하는 hyper parameter
    • 알파값이 클 경우 속도는 빠르지만, 최적의 지점을 뛰어넘어 수렴하지 않을 수 있다.
    • 최적의 지점에 수렴한다. 속도가 느리다 반복값이 늘어들기 때문
    • 러닝레이터에 정답은 없지만, OO 모델이 사용된 논문을 참조하는 것도 방법이다.
  • 경사하각법의 파라미터 한 스텝 업데이트 과정 수식
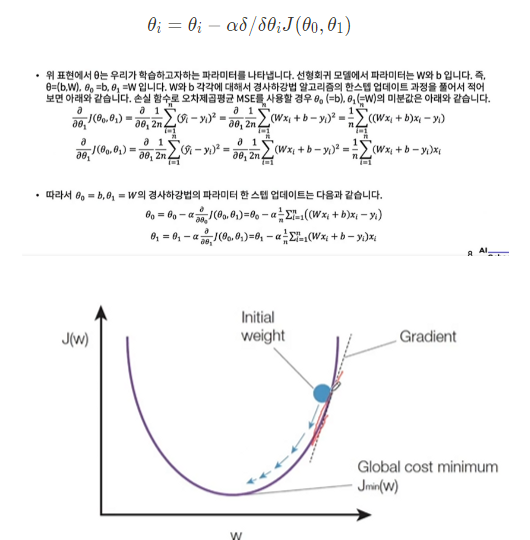
θi=θi−αδ/δθiJ(θ0,θ1)\theta_{i} = \theta_{i} - \alpha\delta/\delta\theta_{i}J(\theta_{0},\theta_{1})

  • 경사하강법은 손실 함수가 최소가 되는 지점에 종료하는 것이 가장 이상적이지만 현실적으로 언제 손실 함수가 최소가 될지 알기 어렵기 때문에 충분한 횟수라고 생각되는 횟수만큼 업데이트를 진행한 후 학습을 종료

2. TensorFlow2.0을 이용한 선형 회귀(Linear Regression)알고리즘 구현

1) 선형 회귀

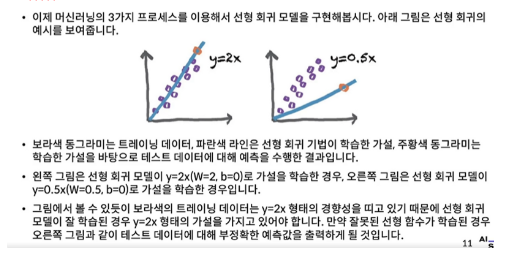
3. Gradient Descent

1) Batch Gradient Descent:

트레이닝 데이터 n개의 손실 함수 미분 값을 모두 더한 뒤 평균을 취해서 파라미터를 한 스텝 업데이트하며 전체 트리이닝 데이터를 하나의 Batch로 만들어 사용하기 때문에 이런 이름이 붙음, 데이터의 갯수가 많으면 한 스 업데이트하는데 많은 시간이 걸리고( 한 스템 업데이트 하는데 전체 배치에 대한 미분값을 계산해야 하므로), 결과적으로 최적의 파라미터를 찾는데 오랜 시간이 걸리게 됩니다.

2) Stochastic Gradient Descent:

한 스텝 업데이트를 진행할 때 1개의 트레이닝 데이터만 사용하는 기법, 파라미터 자주 업데이트할 수 있지만 부정확한 방향으로 업데이트가 진행

3) Mini-Batch Gradient Descent:

위 두가지의 절충, 전체 트레이닝 데이터 Batch가 1000(n)개 라면 이를 100(m)개씩 묵은 mini-betch개수만큼 손실 함수 미분값 평균을 이용해서 파라미터를 한 스텝을 업데이트하는 기법

4. Data

  • 머신러닝 모델은 크게 트레이닝 과정과 테스트 과정으로 나뉩니다. 트레이닝 과정에서는 대량의 데이터와 충분한 시간을 들여서 모델의 최적의 파라미터를 찾습니다.
  • 테스트 과정에서는 트레이닝 과정에서 구한 최적의 파라미터로 구성한 모델을 트레이닝 모델 과정에서 보지 못한 새로운 데이터에 적용해서 모델이 잘 학습됐는지 테스트하거나 실제 문제를 풀기 위해 사용합니다.
  • Test: 모델이 잘 학습 됐는지 체크
  • Interference(추론): 실제 문제를 푸는 과정
  • 검증용 데이터는 트레이닝 과정에서 학습에 사용하지 않지만 중간중간 테스트 하는데 사용해서 학습하고 있는 모델이 오버피팅에 빠지지 않았는지 체크하는데 사용됩니다. 즉, 직관적으로 설명하면 검증용 데이터는 트레이닝 과정 주간에 사용하는 테스트 데이터

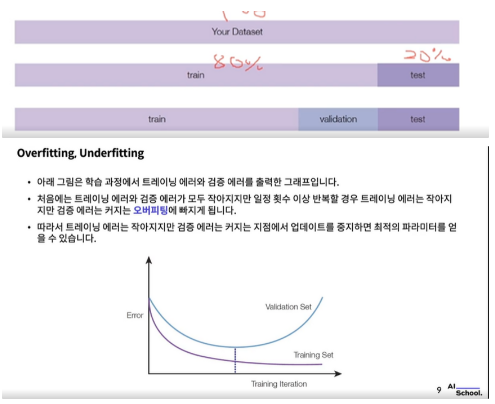
  • 오버피팅: 학습 과정에서 머신러닝 알고리즘의 파라미터가 트레이닝 데이터에 과도하게 최적화 되어 트레이닝 데이터에 대해서는 잘 동작하지만 새로운 데이터인 테스트 데이터에 대해서는 잘 동작하지 못하는 현상
  • 언더피팅: 트레이닝 데이터에도 동작하지 않음, 모델의 표현력이 부족한 것

5. Softmax Regression

  • n개의 레이블을 분류하기 위한 가장 기본적인 model, 모델의 아웃풋에 Softmax함수를 적용해서 모델의 출력 값이 각각의 레이블에 대한 확신의 정도를 출력하도록 만들어주는 기법

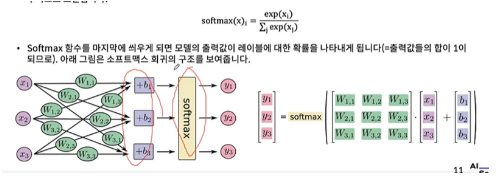
6. Cross_Entropy 손실함수

  • 소프트맥스 회귀를 비롯한 분류 문제에는 크로스 엔트로피Cross-Entropy 손실 함수를 많이 사용. 크로스 엔트로피 손실 함수도 평균제곱오차(MSE)와 같이 모델을 예측 값이 참 값과 비슷하면 작은 값, 참 값과 다르면 큰 값을 갖는 형태의 함수로 아래와 같은 수식으로 나타낼 수 있습니다.
Hy′(y)=−∑iyi′log(yi)H_{y^{'}}(y) = -\sum_iy^{'}_{i}log(y_{i})
  • y’는 참값, y는 모델의 예측값, 일반적으로 분류 문제에 대해서는 MSE보다 크로스 엔트로피 함수를 사용하는 것이 학습이 더 잘 되는 것으로 알려짐

7. MNIST 데이터셋

  • 머신러닝 모델을 학습시키기 위해서는 데이터가 필요함. 하지만 데이터를 학습에 적합한 형태로 정제하는 것은 많은 시간과 노력이 필요한 일. 따라서 많은 연구자가 학습하기 쉬운 형태로 데이터들을 미리 정제해서 웹상에 공개
  • 그 중 MIST 데이터셋은 머신러닝 계의 “Hello World”급
  • 60000장의 트레이닝 데이터와 10000장의 테스트 데이터로 이루어진 데이터셋 0 ~ 9 사이의 28 X 28 크기의 필기체 이미지로 구성

8. One-hot Encoding

  • 범주형 값 Categorical Value을 이진화된 값 Binary Value으로 바꿔서 표현하는 것을 의미
  • 단순한 Integer Encoding의 문제점은 머신러닝 알고리즘이 정수 값으로부터 잘못된 경향성을 학습하게 될 수도 있다는 점. 그러므로 정수를 이진수로 변환된 값으로 범주화 한다.

9. TensorFlow 2.0 케라스 서브클래싱(Keras Subclassing)

1) TensorFlow2.0을 이용한 알고리즘 구현의 2가지 방식

profile
이도현
좋은 지식 나누어요
이전 포스트

섹션2, TensorFlow 2.0 소개

다음 포스트

섹션4, 인공신경망

0개의 댓글