부동소수점
IEEE 754 표준에 따르면 부동소수점을 표현하는 방식에는
- single precision 32비트
- double precision 64비트
2가지가 있습니다.
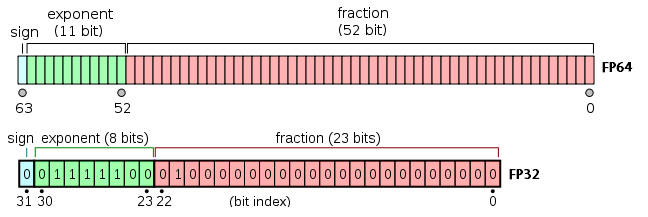
JS에서는 64비트를 사용.
아래 3가지 부분으로 나뉨
- 부호 1비트
- 지수부 11비트
- 가수부 52비트 (나머지)
초과표기법
부동소수점의 지수부를 표현하기 위한 방법.
- 이 bias라는 값을 왜 쓰냐면, 지수가 음수가 될 수도 있어서 그렇습니다.
예를 들면 0.000101이라는 이진수가 있다고 하면
정규화에 대해서 설명할 때 정수부를 1로 만들어야 한다고 했습니다. 그러니까 왼쪽이 아니라 오른쪽으로 소수점을 밀어서 1.01 * 2^-4가 됩니다.
만약 bias가 없어서 -4를 어떻게 표현할까요? 지수부에 부호 비트를 하나 더 만들어야 할까 하지만 이것대로 복잡해집니다.
- 지수부의 비트 수가 N의 경우.
2^(N-1)-1 을 한 수. (매직넘버)
초과표기법으로 인해 두 수의 크기를 비교를 할 경우
(부호가 같으면) 어느 하나의 가수부가 크더라도 지수가 큰 수가 더 큰 값인 것을 알 수 있다.
Hidden bit
2진수의 정규화는 1.xxxx * 2^n의 형태.
가수부를 표현할 때 정규화된 맨 앞의 1을 생략하여 표현 범위를 늘림.
Special value
- 3 초과 표기법이라 가정
0 000 0000(2)을 정규화로 변환 시 : 1.00000 * 2^-3
십진수 : 0.125
즉 0이 0으로 표현 안되어 0으로 약속 하는 것.
아래와 같은 수 그리고 -inf inf nan을 표현합니다.
| 8비트 부동소수점 표현 | 십진수 | |
|---|---|---|
| 가장 작은 양의 실수 | 0 000 0001 | 0.1328125 |
| 가장 작은 음의 실수 | 1 000 0001 | -0.1328125 |
| 가장 큰 양의 실수 | 0 111 1111 | 31 |
| 가장 큰 음의 실수 | 1 111 1111 | -31 |
계산
14.5 (10)
- 이진수로 변환
8+4+2 + 0.05
0.5 2 = 1
1110.1 (2)
1.1101 2^3
64비트
- 부동소수점 표현
지수부 bias : 2^(11-1) - 1 = 1024 -1 = 1023
지수 = 3 + 1023 = 1024 + 2 = 1026
부호 : 0 (양수)
가수 : 1101 (나머지는 0으로 채움)
0 / 1000_0000_001 / 1101 0000 ... 0000
32비트
지수부 bias : 2^(8-1) -1 = 127
지수 = 3 + 127 = 128 + 2
부호 : 0
가수 : 1101
0 / 1000_0010 / 1101 0000 00..000
32비트 부동소수점 변환사이트 : https://www.h-schmidt.net/FloatConverter/IEEE754.html
가장 큰 지수비트
위의 inf nan를 double precision을 기준으로
1111_1111_111 (2)로 지정되어 있기 때문에
가장 큰 지수비트는 1111_1111_110 (2)이다. ( 2^11 -1) = 1023
double precision에서 표현할 수 있는 가장 큰 양의 실수의 경우는
1 X 2^1023 X 1.11111111....
1 X 2^1023 X 2
= 2 ^ 1024
JS에서는 double precision을 사용하므로 표현 할 수 있는 가장 큰 값은
2의 1024 승이다. (Number.MAX_VALUE)
Max Safe Integer
JS에서 Number.MAX_SAFE_INTEGER의 값은 2^53 -1이라고 하는데
왜 이 숫자여야 하나?
64비트에서 52비트의 가수부를 정규화하여 1로 채운다면
1.1111111111..111
즉 53개의 1이 생긴다. (2^53 -1)
그 이상의 수
1.000......0001 의 경우 2^53 +2
1.000......0010 의 경우 2^53 + 4
2씩 증가하여 대소 비교는 가능하나 연산은 불가능하다.
2^53 - 1 이상의 수는 Bigint를 이용.
출처
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=jwyoon25&logNo=221389077105
