일반 선형 회귀

규제를 적용하지 않은 선형 모델

독립 변수(X)의 개수에 따라

1. 단순 선형회귀

$H(x)=Wx+b$

2. 다변수 선형회귀

$H(x_1,x_2,x_3,…,x_n)=W_1x_1+W_2x_2+W_3x_3+⋯+W_nx_n+b$

3. 다항 회귀

회귀가 독립변수의 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현되는 것

기울기 계산 방법에 따라

1. 최소 제곱법

종속 변수(응답 변수) y와 한개 이상의 독립 변수(입력 변수) X와의 상관관계를 모델링 한 것

$Y = ax + b, a = \frac{\sum(x-\bar{x})(y-\bar{y})}{\sum(x-\bar{x})^2}$

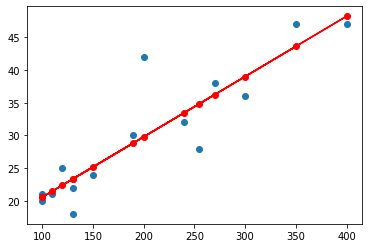
2. 경사 하강법

일단 선형 모델을 그리고 오차를 수정하는 방법

$H(x) = Wx + b$
$cost(W, b)=\frac{1}{m}\sum(H(x)-y)^2$

규제 선형 회귀

Norm(놈; 노름)

벡터 사이의 거리를 놈이라고 부른다.
규제 선형 모델에서 사용하는 Norm은 $L_2$과 $L_1$이다.

• $L_2$ : 유클리드 거리 → 일반적인 거리 함수
• $L_1$ : 맨해튼 거리; 택시 거리

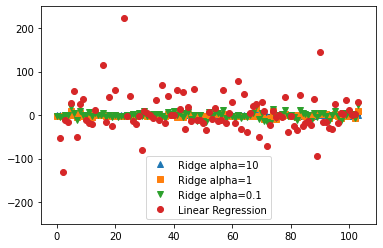
1. Ridge(릿지) 회귀

• 평균 제곱 오차식에 alpha항이 추가
• 학습한 가중치의 제곱을 규제항($L_2$ 규제) 사용
• 편향(bias)를 조금 손해 보면서 분산(Variance)을 줄여 성능을 향상

  $cost(W, b) = MSE + α(L_2Norm)$
  $= \frac{1}{m}\sum(H(x)-y)^2+α\sum^n_{j=1}W^2_j$

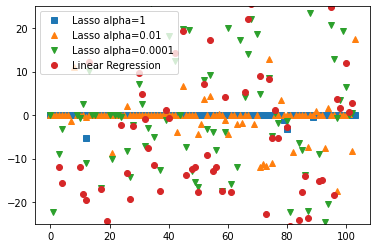
2. Lasso(라쏘) 회귀

• Ridge 회귀의 단점을 해결하기 위해 대안으로 나온 방법
• 학습한 가중치의 절대값의 합을 규제항으로 사용

  $cost(W, b) = MSE + α(L_1Norm)$
  $= \frac{1}{m}\sum(H(x)-y)^2+α\sum^n_{j=1}|W|_j$

3. Elastic Net(엘라스틱 넷)

• 선형 회귀에 2가지 규제항($L_1$규제항, $L_2$규제항) 추가

  $cost(W, b) = MSE + α_1(L_1Norm) + α_2(L_2Norm)$
  $=\frac{1}{m}\sum(H(x)-y)^2+α_1\sum^n_{j=1}W^2_j+α_2\sum^n_{j=1}|W|_j$

4. 조기 종료

경사 하강법과 같은 학습 알고리즘을 수행 할 때,
검증 에러가 최소값에 도달하면 바로 훈련을 중지 시키는 규제 방법