[모노토닉 큐] 징검다리 여행하기

문제 파악하기

https://school.programmers.co.kr/learn/courses/30/lessons/64062

위의 문제를 요약하면 다음과 같다.

사람들이 징검다리를 건너는데 모든 돌을 한번씩 밟아야 하고, 돌을 밟을 때 돌을 밟을 수 있는 횟수가 줄어든다. 이 때 k가 주어지는데 k는 돌을 k -1 개 스킵하고 건널수 있는 최대 갯수이다. 예를 들면 k가 3이면 1 2 0 0 3 은 뛸 수 있지만 1 2 0 0 0 3 은 뛸 수 없다.

이 문제는 바꿔서 생각하면 다음과 같이 생각할 수 있다.
1. k 구간을 정해서 1칸씩 순회하되, k 구간 중 최대값을 가져온다.
2. 가져온 값을 결과값과 비교하고, 그 중 작은 값을 결과 값으로 업데이트한다.

이렇게 푸는 것이 가능한 이유는 돌이 0이여도 건너 뛸 수 있는데 해당 구간에서는 최대 돌 수치 만큼 뛰는 것이 가능하다. 그러나 다른 구간에서는 그것 보다 적은 수치만 허용 가능하다면, 결국 모든 다리를 건너기 위해서는 그 중 작은 값을 업데이트해야하기 때문이다.

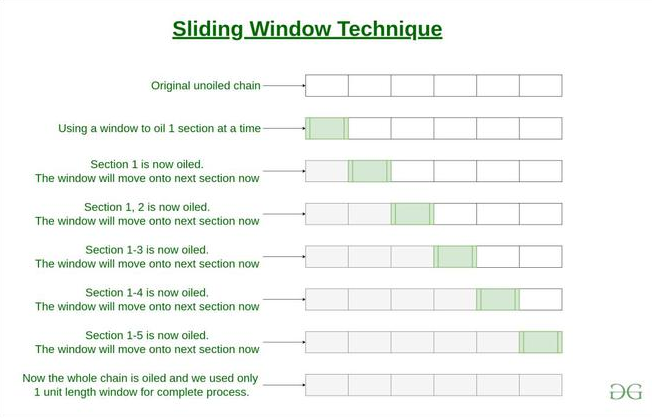
슬라이딩 윈도우

슬라이딩 윈도우는 구간 단위로 순회하면서 구간안에서 어떤 값을 얻고자 할 떄 쓰인다.
보통 구간 내의 최대값과 최소값을 얻을 때 사용한다.

슬라이딩 윈도우의 시간 복잡도는 O(NK)이다. 그 이유는 배열을 N번 순회하는데, 배열 안에서 최대, 최소값을 얻기 위해 K번 또 순회하기 때문이다.

슬라이딩 위도우 설명 영상

최대, 최소값을 좀 더 효율적으로 구할 필요성

해당 알고리즘의 문제는 시간 복잡도가 O(NK)라는 점이다. 이것은 K가 최악의 경우 N과 같아지는 데, 그 경우 $O(N^2)$의 시간 복잡도를 가지게 된다. 이를 해결하기 위해서는 PriorityQueue, 또는 모노토닉 큐를 이용하면 $O(N)$의 시간복잡도로 최적화가 가능하다.

모노토닉 큐

모노토닉 큐가 가장 많이 쓰이는 경우는 구간 내 최대, 최소를 구할 때 많이 쓰인다. 즉, 우리가 사용하고자하는 slidingwindow 알고리즘에 효과적으로 사용가능하다는 뜻이다.

다음은 모노토닉 큐를 사용하는 코드이다.

public class SlidingWindow {

    private final int[] arrays;

    public SlidingWindow(int[] arrays) {
        this.arrays = arrays;
    }

    public void slideMax(int k) {
        Deque<Integer> dq = new ArrayDeque<>();
        for (int i = 0; i < arrays.length; i++) {
            // dq에 들어있는 값이 현재 값보다 작으면 제거
            // 이 작업을 통해 모노토닉한 dq를 유지할 수 있다.
            while (!dq.isEmpty() && arrays[dq.getLast()] < arrays[i]) {
                dq.removeLast();
            }
            // dq에 들어있는 인덱스 값이 k 범위를 벗어나면 제거
            // 구간을 만들기 위해서 필요한 작업
            if (!dq.isEmpty() && dq.getFirst() <= i - k) {
                dq.removeFirst();
            }
            dq.addLast(i);
            // i 가 k번 진행한 이후 부터 최대값을 가져온다. 맨 위에 모노토닉하게 만드는 while문 어떻게 만드는가에
            // 따라서 최소값을 얻어올 수도 있다.
            if (i >= k - 1) {
                System.out.println(arrays[dq.getFirst()]);
            }
        }
    }
}

예제를 위해 간단한 SlidinWindow 클래스를 만들었다. 코드를 보시다시피 for문 하나로만 동작하고, 시간 복잡도는 $O(N)$임을 알 수 있다.

문제 해결하기

monotonicqueue를 사용해서 문제를 해결한 코드는 다음과 같다.

import java.util.ArrayDeque;
import java.util.Deque;

class Solution {

    public int solution(int[] stones, int k) {
        Deque<Integer> dq = new ArrayDeque<>();
        int answer = Integer.MAX_VALUE;

        for (int i = 0; i < stones.length; i++) {
            while (!dq.isEmpty() && stones[dq.getLast()] < stones[i]) {
                dq.removeLast();
            }
            if (!dq.isEmpty() && dq.getFirst() <= i - k) {
                dq.removeFirst();
            }
            dq.addLast(i);
            if (i >= k - 1) {
                answer = Math.min(answer, stones[dq.getFirst()]);
            }
        }
        return answer;
    }
}