[231N] Lecture 3,4 review
Leture 3 | Loss Functions and Optimization
3번째 강의에서는 손실함수와 최적화에 대해 배운다.
나는 동시에 224N강의를 듣고 있고, 224 n에서 배운 내용이 다시 231n에 나와서 뭔가 복습을 하는 느낌도 있다.
하지만 솔직히 강의력은 231n이 더 좋고 이해가 잘된다. 뭔가 224n에서 내가 많이 땅굴을 파고 굴러서인지 뭔지 아무튼 더 이해가 잘되어서 좋았다.
근데 교수님이 좀 말이 빠르시다. ㅎㅎ
Loss functions
그럼 손실 함수에 대해서 알아보자.
확실히 이 강의는 예를 들어 설명을 하는데, 나는 이쪽이 더 이해가 쉽게 잘 되는 편 같다.
우리는 CIFAR-10을 통해 한 이미지를 10개의 클래스로 나누지만, 사실 10개로 예를 들기엔 너무 많고 복잡하기 때문에 3개로 예를 들어 설명해보자.

여기 한 그림에 대한 분류 점수가 있다.
첫번째 그림인 고양이에 대해 cat 점수는 3.2이고 car점수는 5.1이다. 즉 점수로 따지면 이 이미지에 대해 자동차로 인식하는 점수가 더 높기에, 좋은 분류는 아니라고 할 수 있다.
그에 반해, 두번째 그림인 자동차 이미지에 대해 자동차 점수는 다른 클래스 점수에 비해 월등히 높다.
마지막 개구리 이미지는 최악임을 알 수 있다.
우리는 이런 분류 점수를 통해서, 잘 분류를 했는지를 점수화하고 싶다.
이를 손실 함수를 통해 할 수 있다.
손실함수가 적으면 우리는 잘 분류를 한 것이고, 만약 손실 함수가 크면 분류를 잘 못한 것이다.
여기서 손실 함수를 L이라고 하면 우리는 손실 점수를 얻을 수 있다.
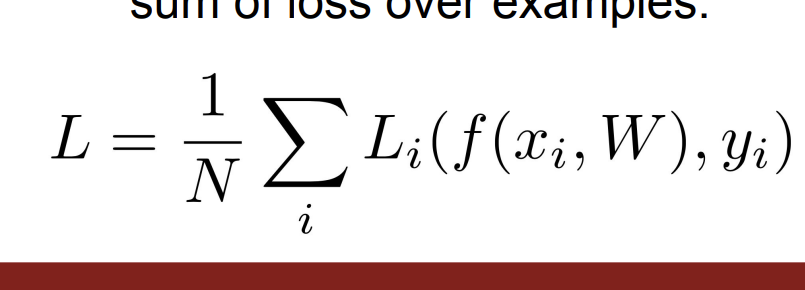
이런 손실 함수를 첫번째 예시로 SVM loss를 들어 설명해보겠다.
SVM LOSS
SVM 손실 함수는 다음과 같은 형식이다.

만약 현재가 고양이 이미지라면, 고양이 클래스가 가 된다. 그리고 다른 클래스의 점수가 가 된다.
다른 클래스의 점수 + 1 이 현재 클래스의 점수보다 크게 되면
다른 클래스의 점수 - 현재 클래스의 점수 + 1이 손실함수가 된다.
이는 Hinge loss라고도 한다. 그래프의 모양 때문이다.
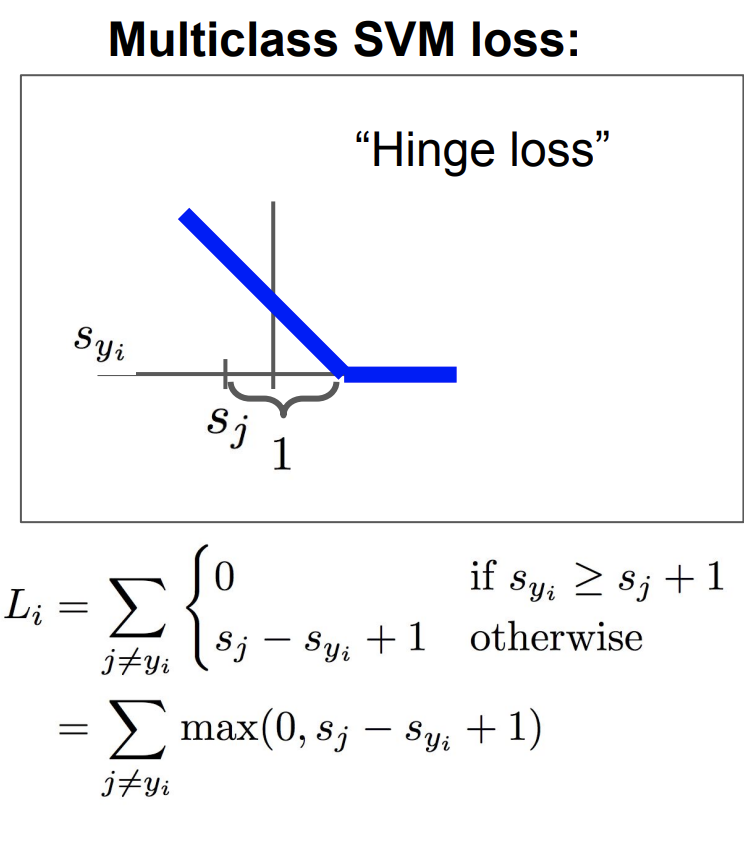
즉 이전 고양이에 대한 손실 점수를 구해보면
L = max(0, 5.1-3.2+1) + max(0,-1.7-3.2+1)
= max(0, 2.9) + max(0, -3.9)
= 2.9 + 0 = 2.9
2.9가 된다.
자동차에 대한 손실 점수는
L = max(0, 1.3 - 4.9 + 1)
+max(0, 2.0 - 4.9 + 1)
= max(0, -2.6) + max(0, -1.9)
= 0 + 0 = 0
0이다.
개구리에 대한 손실 점수는
= max(0, 2.2 - (-3.1) + 1)
+max(0, 2.5 - (-3.1) + 1)
= max(0, 6.3) + max(0, 6.6)
= 6.3 + 6.6 = 12.9
즉 가장 손실 점수가 낮은 것은 자동차, 높은 것은 개구리다.
그래서 우리는 모든 손실점수들을 더한 뒤 개수로 나눈다.
L = (2.9 + 0 + 12.9)/3
= 5.27
따라서 평균 손실 점수는 5.27이 된다.
여기서 질문들이 몇개 있다.
Q. 만약 자동차의 점수가 살짝 달라지면?
A. 달라지는 것 없이 여전히 점수가 0이 된다. 왜냐하면 다른 점수들과 차이가 확실히 크기 때문이다.
Q. 가능한 min/max 손실은 몇점인가?
A. min = 0 max = 무한이다.
Q. 맨처음 W행렬이 거의 0이면 손실점수는 어떻게 계산되는가?
A. 점수들이 0이 대부분이라면, 손실 점수는 1에 가까울 것이다. 왜냐하면 우리는 max( - + 1)을 함수로 했기 때문이다.
Q. 만약 현재 클래스 또한 포함하여 더하면 값이 어떻게 변하는가?
A. 합의 값은 1씩 증가한다.
Q. 그럼 현재 클래스 또한 포함하여 더한 뒤 평균을 내면 어떻게 값이 변하는가?
A. 평균은 변하지 않는다.
Q. 만약 우리가 제곱을 사용하면 이전 함수와 다른이 있나? max( - + 1)^2
A. 다르다. 값이 더 극대화된다.
Q. 만약 손실이 0이 되는 W값을 찾으면, 이 행렬은 유일한가?
A. 아니다. 유일하지 않다. 2W도 손실이 0이 된다.
정규화
이전 224N의 5,6 리뷰 블로그를 확인하면 여기도 정규화라는 내용을 다룬다. (사실 이 글을 쓰는 시점에서 어제 배웠다.)
우리는 누누히 말하지만, 훈련 데이터에서 딱 들어맞는 것은 별로 중요하지 않다. 테스트 데이터에서 성능이 좋아야한다.
즉 과적합을 이유로 우리는 정규화를 해야한다.
여기서 정규화는 모델이 좀 더 "간단"하게 만든다. 그래서 더 테스트 데이터에 잘 맞게 한다.
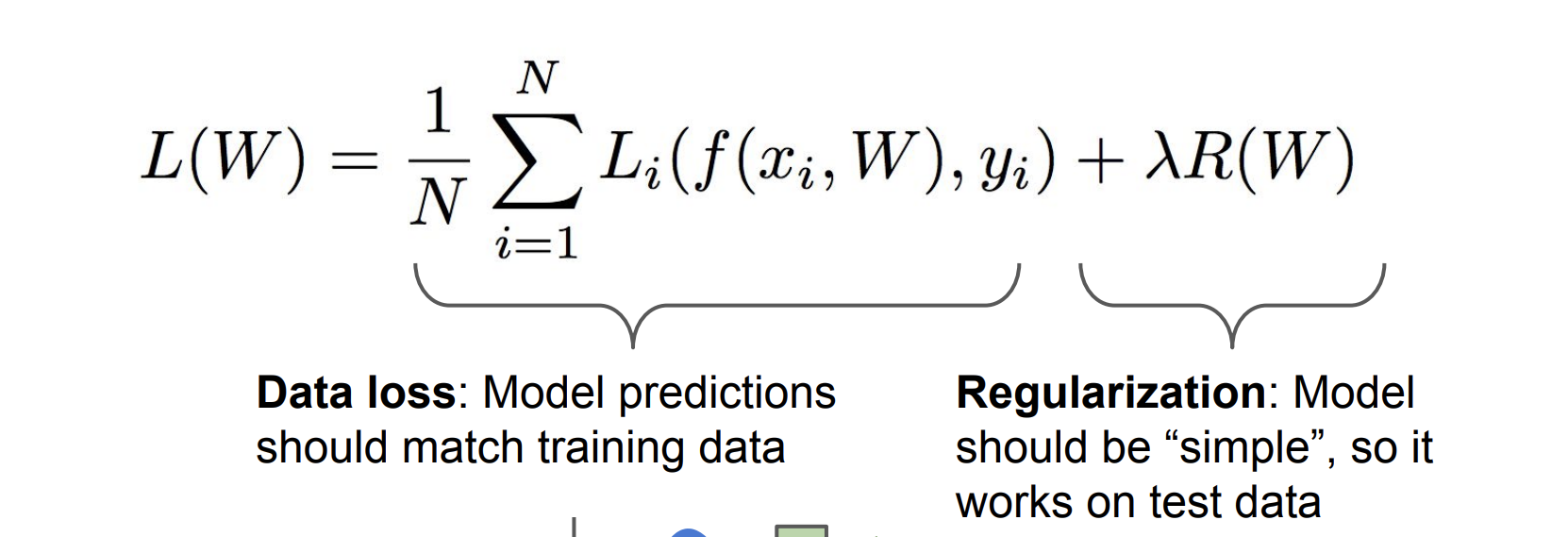
손실 함수는 Data loss + Regularization 으로 구성된다.
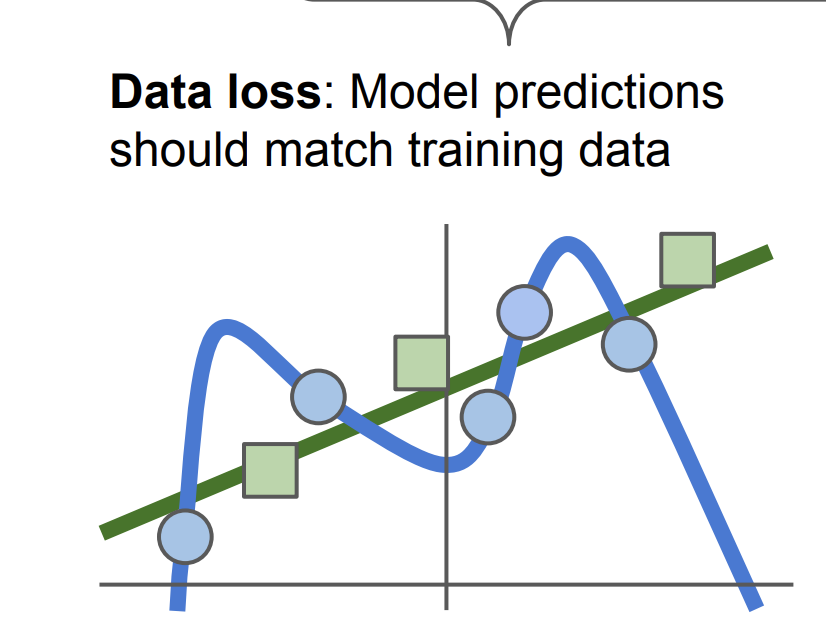
즉 파란선의 구불거리는 선은 훈련 데이터에 모두 적합하지만 초록색의 테스트 데이터에 하나도 맞지 않는다. 즉 파란선보다 녹색선을 만들어야 한다.
정규화에 대해서 가장 많이 사용하는 것은
L2, L1, Elastic net, Max norm regularization, Dropout 등등이 있다.
여기서는 L2, L1에 대해서 설명한다.
어떤 정규화를 선택했는지에 따라서 선호하는 W가 다를 수 있다.
여기서 L2를 예를 들어보자.

첫번째 w1에 대한 점수는
(1-1)^2 + (1-0)^2+ (1-0)^2+ (1-0)^2 = 3
두번째 w2에 대한 점수는
(1-0.25)^2 + (1-0.25)^2 + (1-0.25)^2 + (1-0.25)^2 = 2.25
즉 두번째 점수가 낮다.
L2 정규화는 W2를 더 선호한다. x의 모든 다른 값에 분산시키는 것을 더 선호한다.
반대로 L1 정규화는 W1을 더 선호한다.
하지만 여기 예시에서는 둘 다 1이니 좋은 예시가 아니다.
일반적으로 W1는 희소 솔루션을 더 선호한다고 한다.
여기서 더 많은 이야기를 하자면, L1 정규화는 가중치를 축소하는 효과를 가지고 있다. 가중치의 절대값을 줄일려는 경향이 있다. 이 경향은 가 커질수록 강해진다.
가중치의 절대값 합이 비용함수의 일부가 되기 때문에 가능한 적은 수의 가중치에 의존하려고 한다. 그에 반해 L2 정규화는 가중치의 크기는 줄이지만 완전히 0으로 만들지는 않는다고 한다.
이 이유는 무엇일까? 바로 미분가능성 때문이다.
우리가 손실함수에서의 최소값을 구하기 위해서 미분을 하여 극소값을 구한다.
L2 정규화를
J = MSE() +
라고 하면,
L2 정규화에서의 그레디언트는
2 이다.
그래서 L2 정규화의기울기는 항상 에 비례한다.
이는 가중치는 줄어들지만 완전히 0이 되지 않는다는 것을 의미한다.
그럼 이제 Softmax 손실 함수에 대해 알아보자.
Softmax Classifier
이전까지 배운 SVM 함수는 점수에 대한 해석이 따로 없었다. 우리는 이제 점수에 대해 의미를 부여해보자.
Softmax 함수는 다음과 같다.
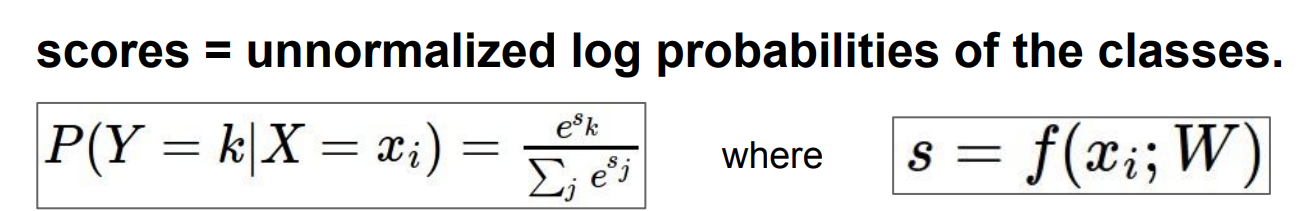
하지만 함수를 바로 사용하는 것은 무리다. 이미 지수함수를 사용한 이상 너무 큰 수가 나오기 때문에 이를 낮춰줄 로그 함수를 먼저 취한 후, 손실 함수는 값이 작을 수록 좋기 때문에 마이너스를 취한다.
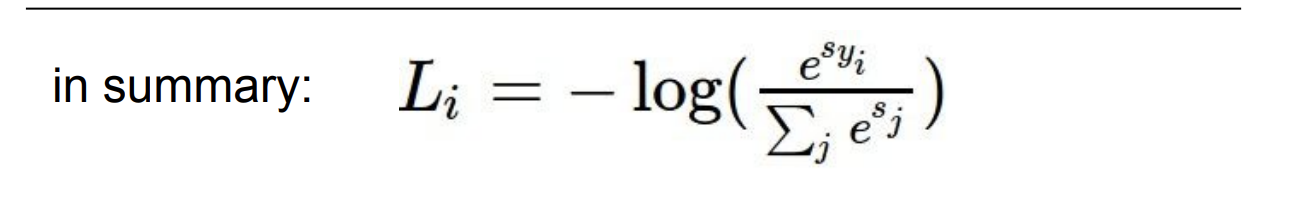
그리고 마이너스 로그 함수의 그래프 개형은 다음과 같다.
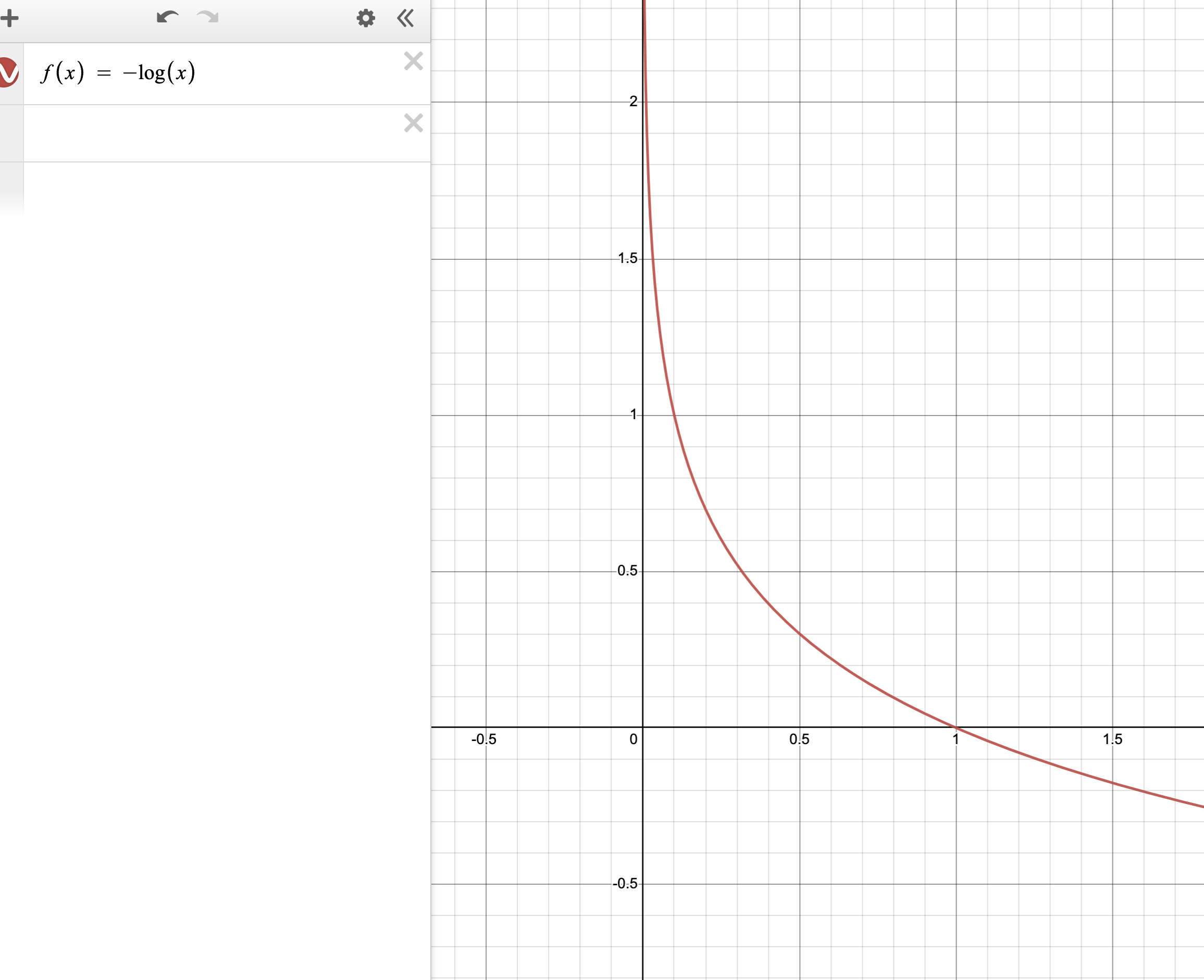
그래서 이전 고양이 클래스에 대한 손실 점수를 한번 구해보자.
일단 고양이 클래스의 점수들을 모두 e승을 취한다.
여기서 이다.
즉 지수를 취함으로 모든 값을 양수로 만들 수 있다.

그 다음 정규분포로 만든다.
모든 클래스의 값의 합을 1로 만든다.

그럼 값이 확률이 된다.
이를 손실 함수에 대입한다.

아까 로그 함수는 1이하의 값에 대해 감소하는 모양을 그렸다.
즉 확률이 낮을수록 손실은 크고, 확률이 높을 수록 손실은 작아진다.
여기서도 질문이 생길 수 있다.
Q. 손실함수에 대한 min/max 값은 무엇인가?
A. 최소값은 0이고 최대값은 무한대이다.
Q. 만약 맨처음 W의 값을 초기화하여 대부분 0일 때의 손실값은?
A. -log(1/n) = log(n) 이 될 것이다.
SVM vs Softmax
그럼 이 두 분류기를 한번 비교해서 보자.
SVM은 어느정도 점수가 다른 클래스 보다 크면 어떤 점수를 가지던 손실 점수는 그대로임을 알 수 있다.
반면에 Softmax는 항상 모든 단일 데이터 포인트를 지속적으로 개선하면 더 좋은 점수를 가질 수 있다.
그럼 지금까지 좋은 분류를 하기 위한, 즉 손실 점수를 낮추는 W를 어떻게 구할 것인가?
바로 최적화를 통해 구할 수 있다.
Optimization
교수님은 여기서 최적화를 이런 그림을 통해 비유했다.

이 계곡에서의 가장 평평한 지점을 찾기 위해서 우리는 계속 걷고 걷는 것이다.
이러한 방법 중 하나는 (가장 멍청한 방법이기도 하다.) Random search이다.
즉 그냥 무작위로 W의 값을 설정해서 계산해보는 것이다.
운이 좋으면 바로 답을 찾을 수 있지만, 너무 시간이 오래 걸린다.
두번째 방법은 Follow the slope 방법이다.
이 방법은 산 비탈길에서 서서 발로 지평을 느끼고 가장 비탈길의 경사가 가파른 내리막길을 찾아 그 방향으로 가는 것이다.
이를 우리는 똑똑하게 미분을 통해 구할 수 있다.
그럼 우리는 미분을 하기 전에, 무식하게 h를 0.0001(아주 작은 값)으로 설정해서 한번 미분값을 구해보자.

이렇게 처음 W의 값에서 0.0001을 더한 뒤 손실 점수를 구하면 아주 조금 손실 점수가 줄었다는 것을 알 수 있다.
이를 통해 gradient dW를 구할 수 있다.
이렇게 모든 dW를 구할 수 있지만 알다시피 너무나 바보같은 방법이다.
우리는 미분을 통해 바로 구할 수 있다.
이것이 바로 경사 하강법이다.
Gradient Descent
그림에서의 빨간 부분은 손실 점수가 낮은 지역이고 파랑, 보라 부분은 손실 점수가 높은 지역이다.
한 지점에서의 미분을 통해 negative 한 방향으로 점을 조금씩 이동시켜서 우리는 손실 점수가 가장 낮은 지역을 찾아갈 수 있다.
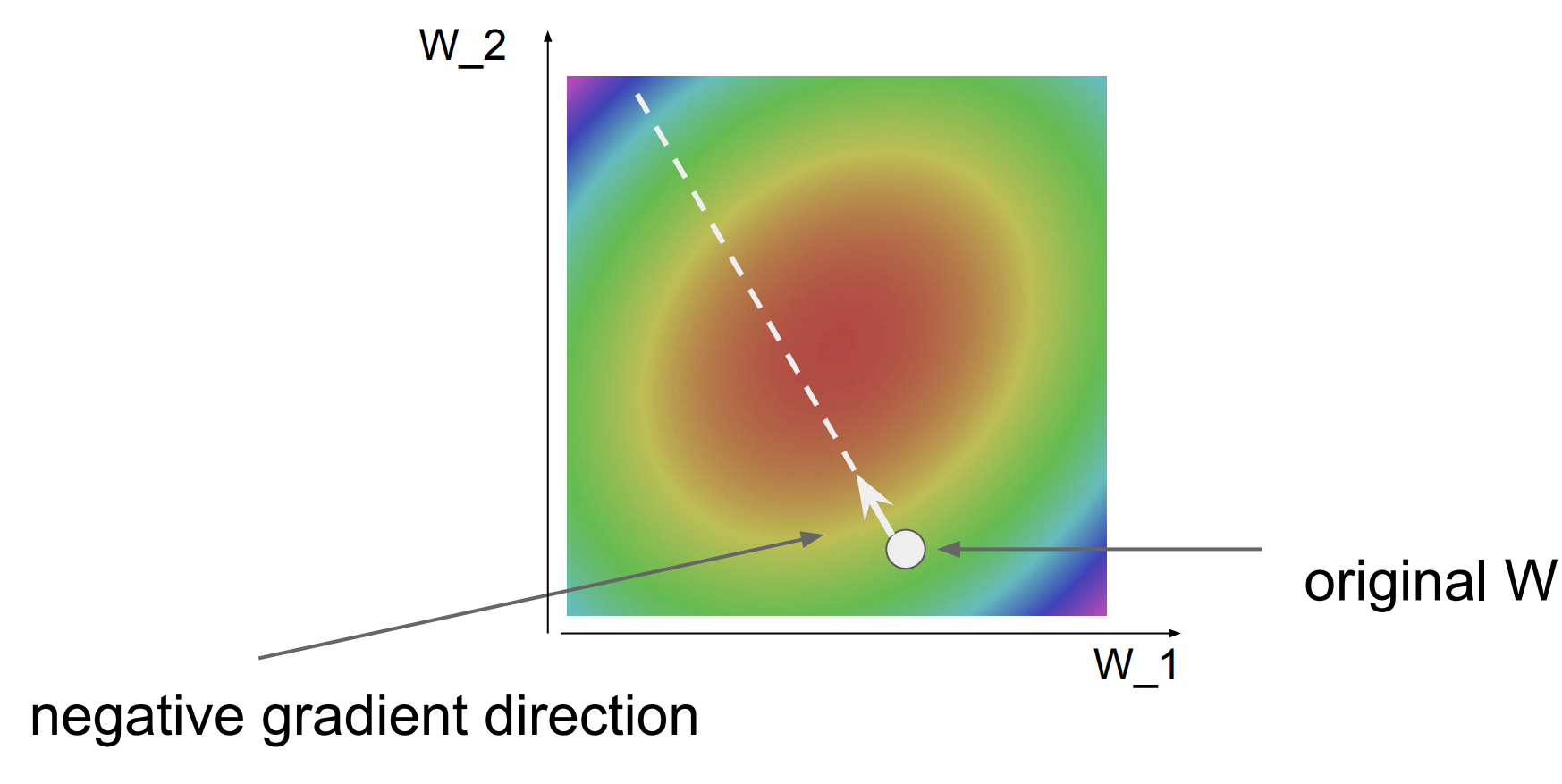
코드로 나타내면 다음과 같이 작성한다.
while True :
weights_grad = evaluate_gradient(loss_func, data, weights)
weights += -step_size * weights_grad여기서 step_size는 발자국의 크기라고 생각하면 된다. 방향은 정했는데 얼마나 크게 이동해야 할지 정하는 것이다.
이를 학습률이라고도 한다.
Stochastic Gradient Descent
줄여서 SGD라고도 한다. 모든 경사를 구할 수 없으니 일부(minibatch)만 확인해서 구한다는 것이다.
이전 경사하강법보다 속도면에서 뛰어나다.
while True :
data_batch = sample_training_data(data, 256)
weights_grad = evaluate_gradient(loss_func, data_batch, weights)
weights += -step_size * weights_grad일단 여기까지 lecture 3을 정리한다.
Lecture 4 | Introduction to Neural Networks
4강에서는 Backpropagation 과 Neural Networks에 대해 배운다.
이미 224N에서 역전파에 대해 배웠지만 여기서 또 배우니 복습하는 기분인데, 여기서 더 많은 예제에 대해 배워서 좋았다.
역전파는 복잡한 함수의 식의 미분값을 계산하기 복잡하니까 함수를 더하기, 곱하기로 쪼개서 편미분을 통해 미분값을 구하기 쉽도록 하는 방법이다.
간단한 예시를 통해 살펴보자.
Backpropataion
역전파에 대해서 자세한 설명은 224N lecture 3을 참고하면 좋을 것 같다.
요약하면 역전파는 Downstream gradient = local gradient * upstream gradient가 된다. 왜냐하면 체인 규칙 때문이다.
Example 1
첫번째 예시를 풀어보았다.

Example 2
두번째 예시를 풀어보았다.
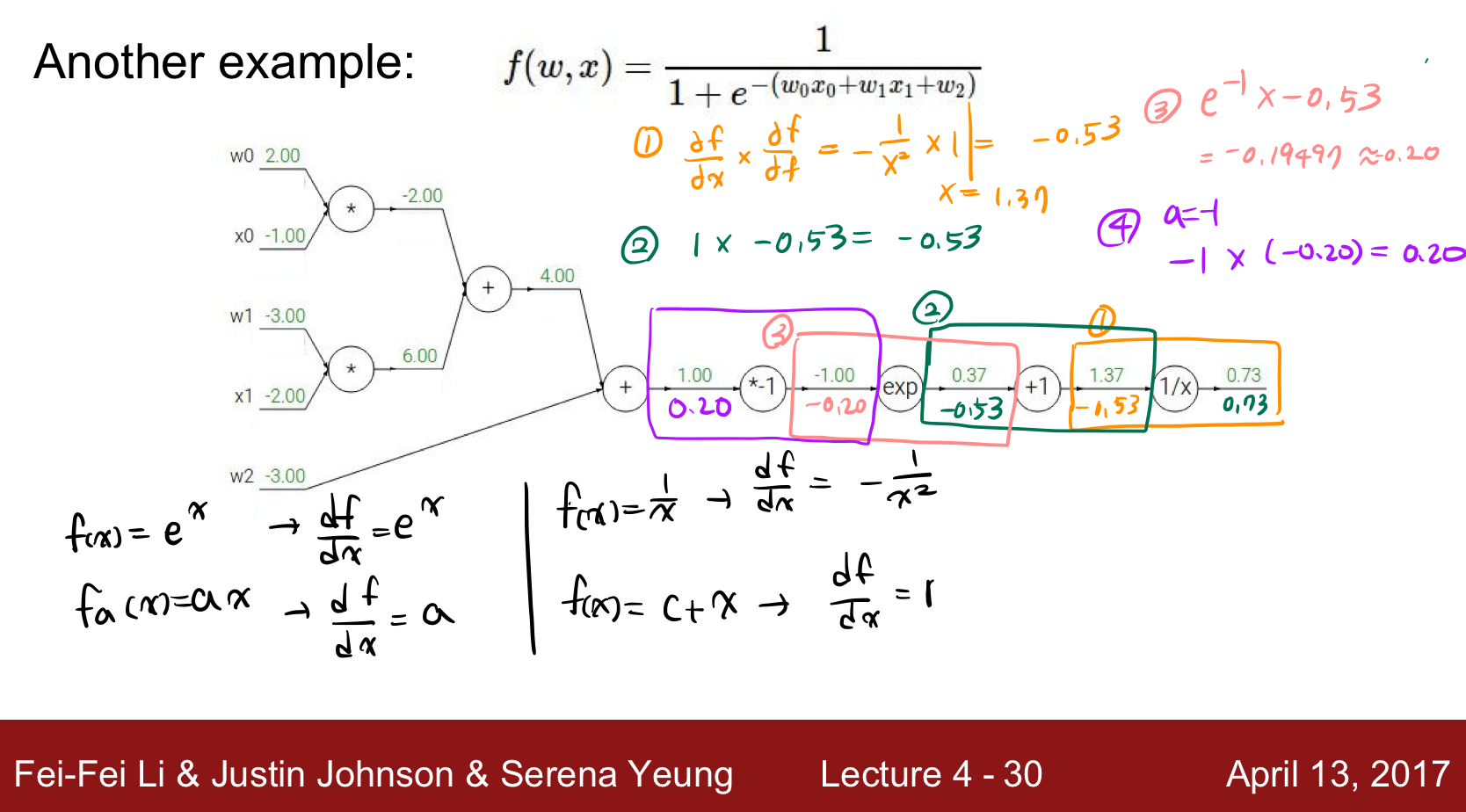
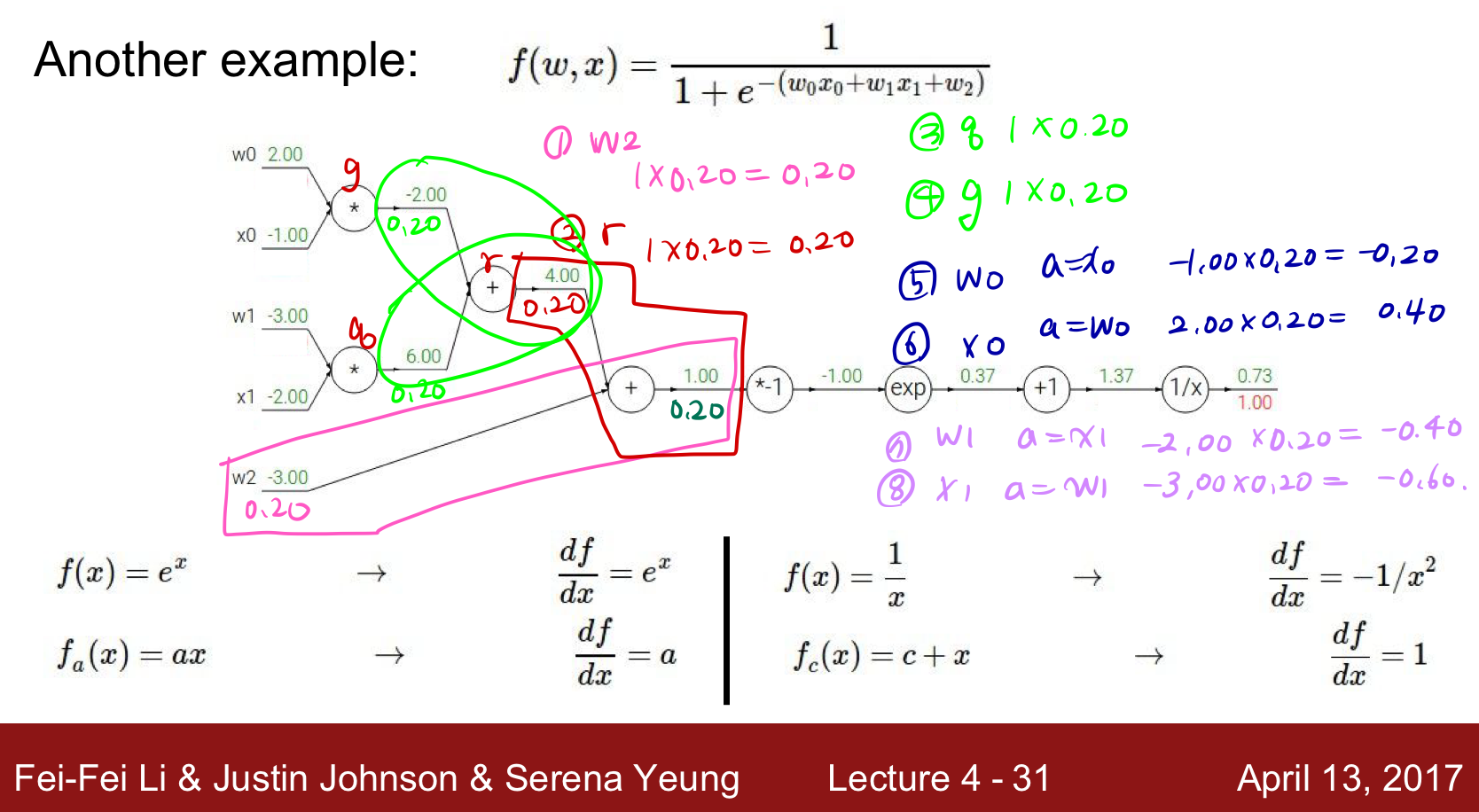
Patterns in backward flow
역전파를 통해 우리는 몇가지 패턴을 찾을 수 있었다.
- add gate : gradient distributor
- max gate : gradient router
- mul gate : gradient switcher
Example 3
그럼 벡터화된 코드에 대한 기울기는 어떻게 구할까?
local gradient 는 자코비안 행렬이 된다.
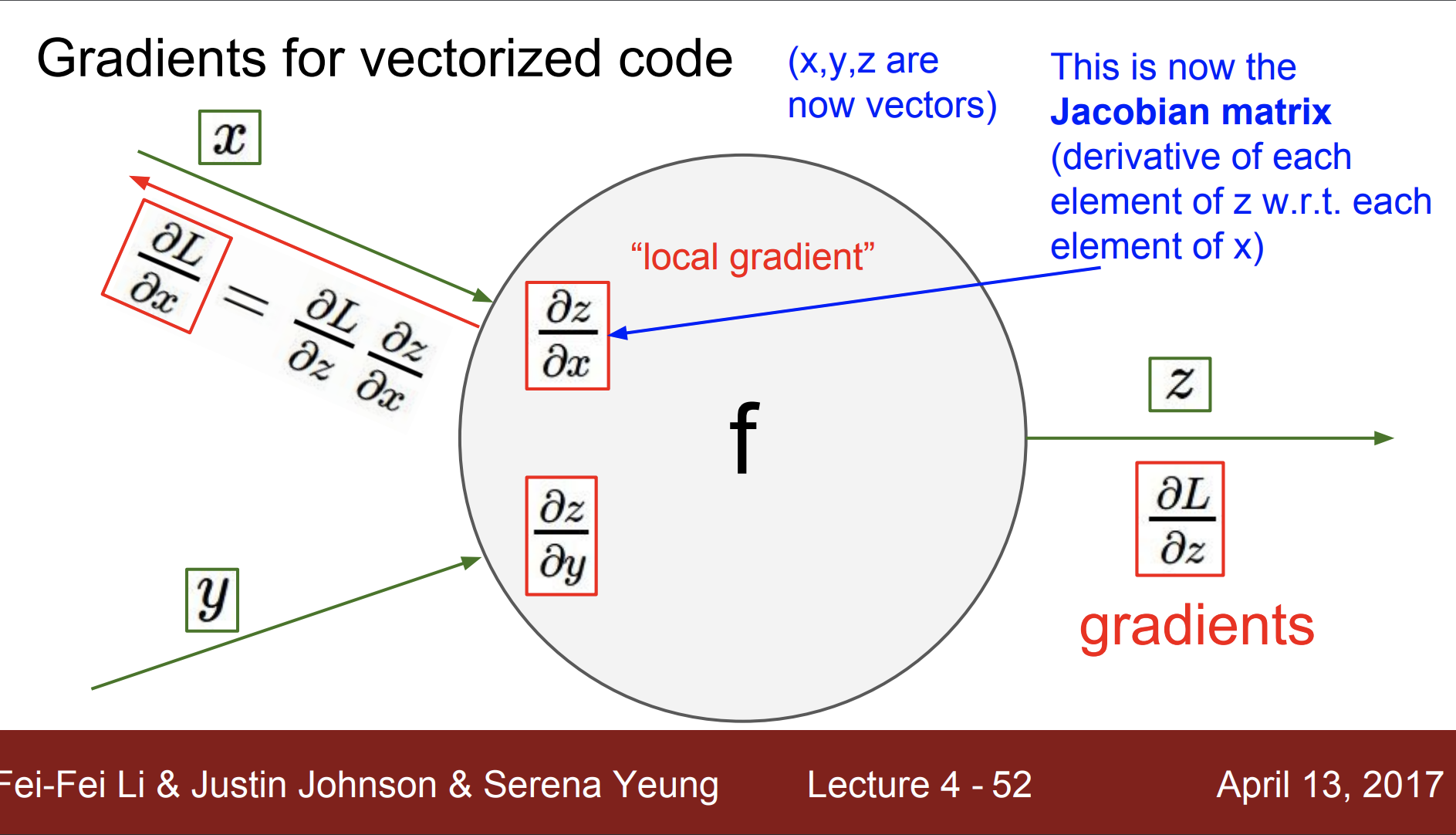
자코비안 행렬을 간단하게 살펴보면,

이런 형태이다.
그럼 자코비안 행렬의 크기는 어떻게 되는가?
만약 input vector가 4096이라면 4096 * 4096이 된다.
그럼 자코비안 행렬의 모양은 어떻게 되는가?
대각 행렬이 된다.
그러니까 두번째 output 벡터와 첫번째 input 벡터를 편미분하면 0이된다는 소리다. 흠 이에 대해서는 좀 더 알아봐야 할 것 같다 😈
그럼 세번째 예시에 대해 직접 풀이해보자.
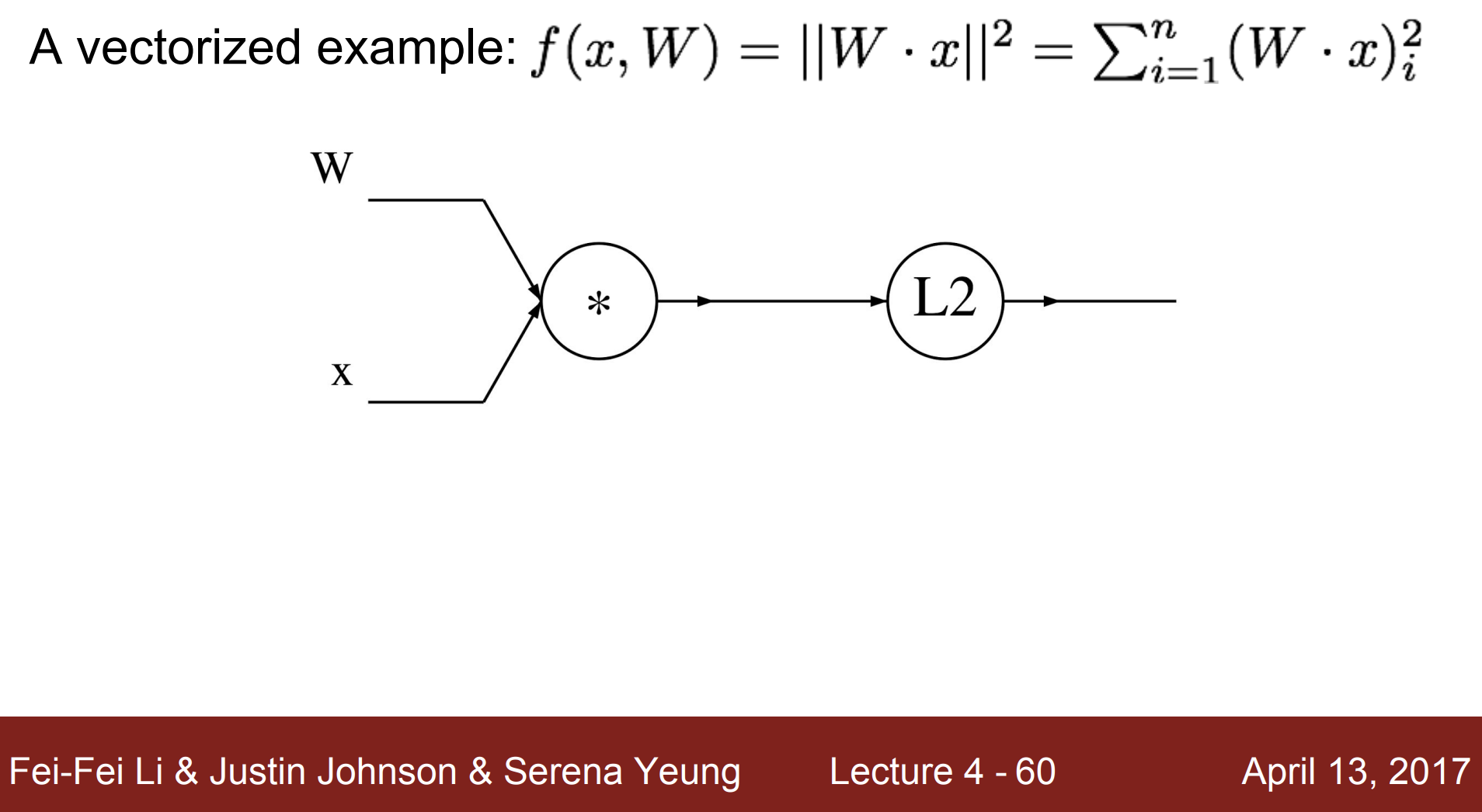
먼저 forward 하게 계산한다.
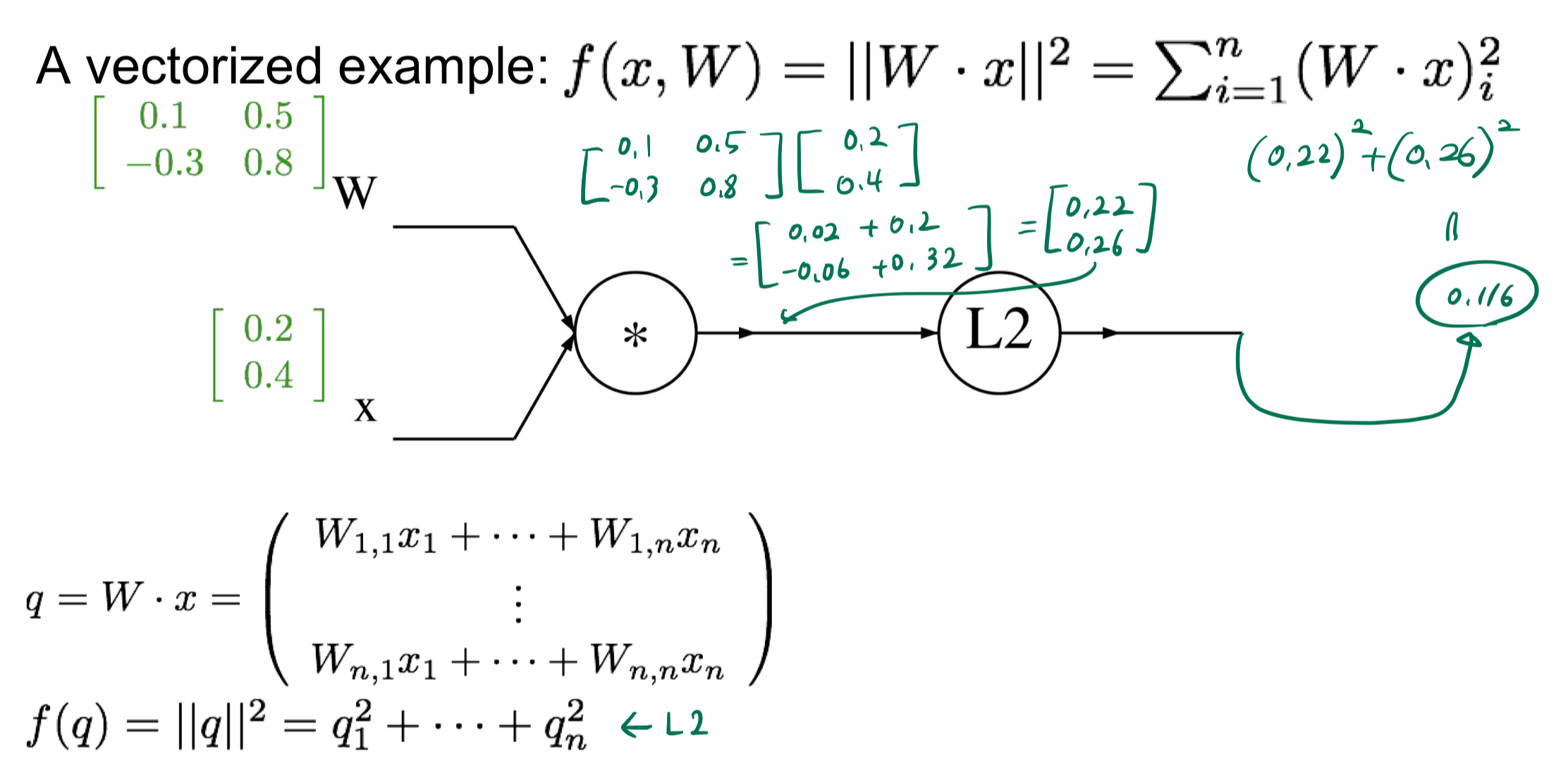
그 다음 backward에 대해 살펴보자.
우선
f에 대한 q의 편미분은 2q이다.
즉 q에 2를 곱한 값이다.
그리고 q에 대한 xi의 편미분은 이다.
q에 대한 의 편미분은 이다.
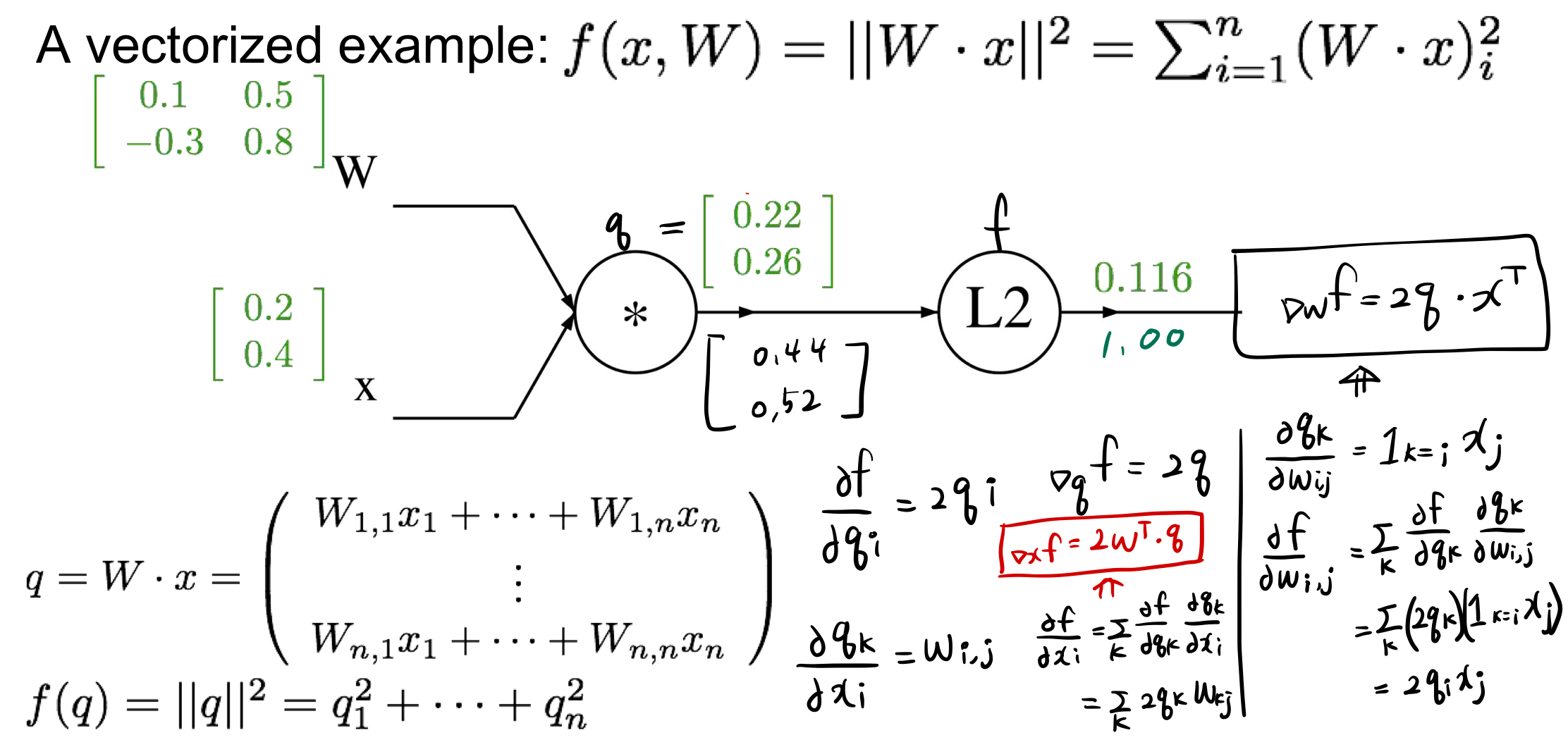
위에서 구한 식대로 W, x의 미분값을 구했다.
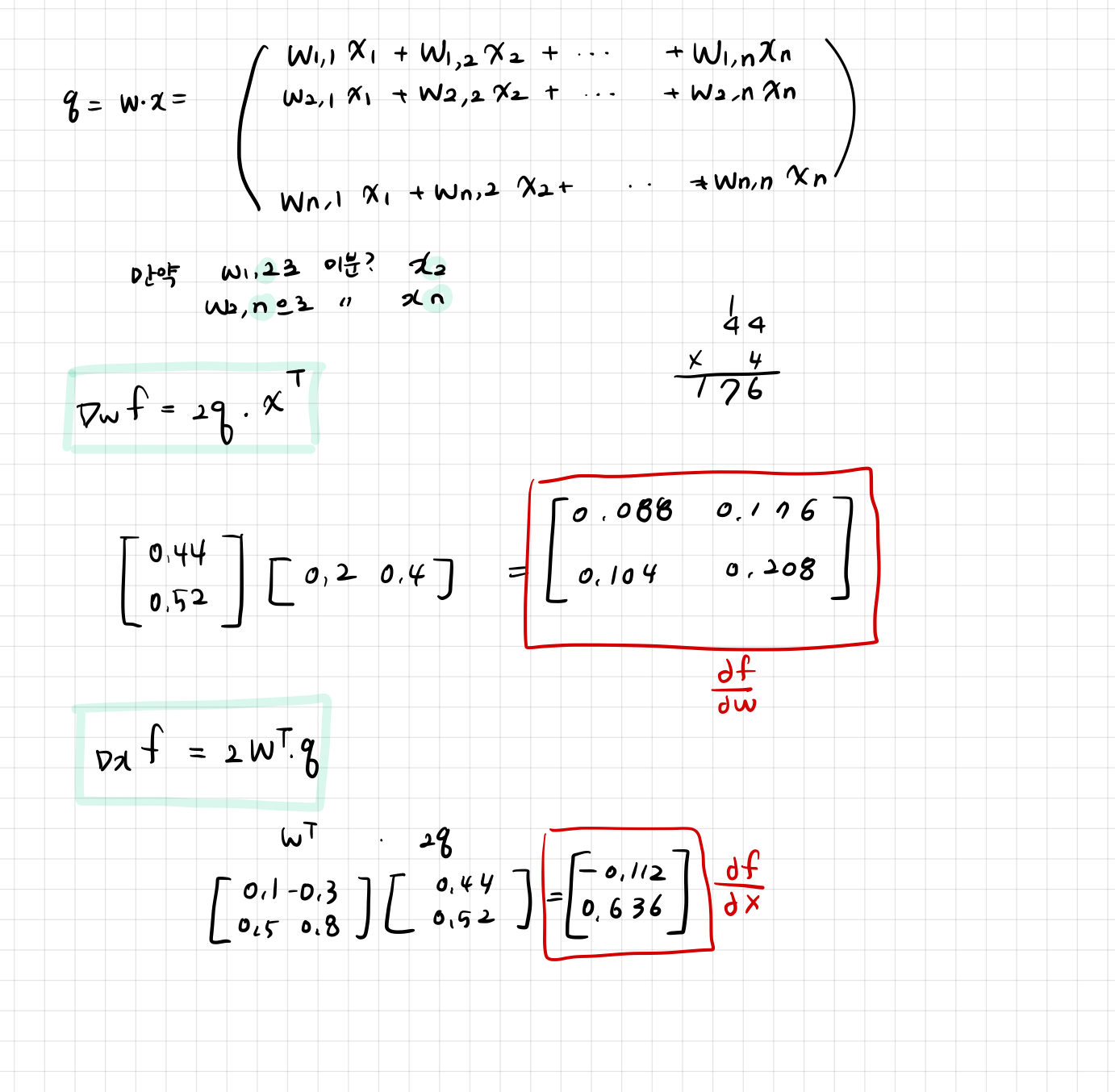
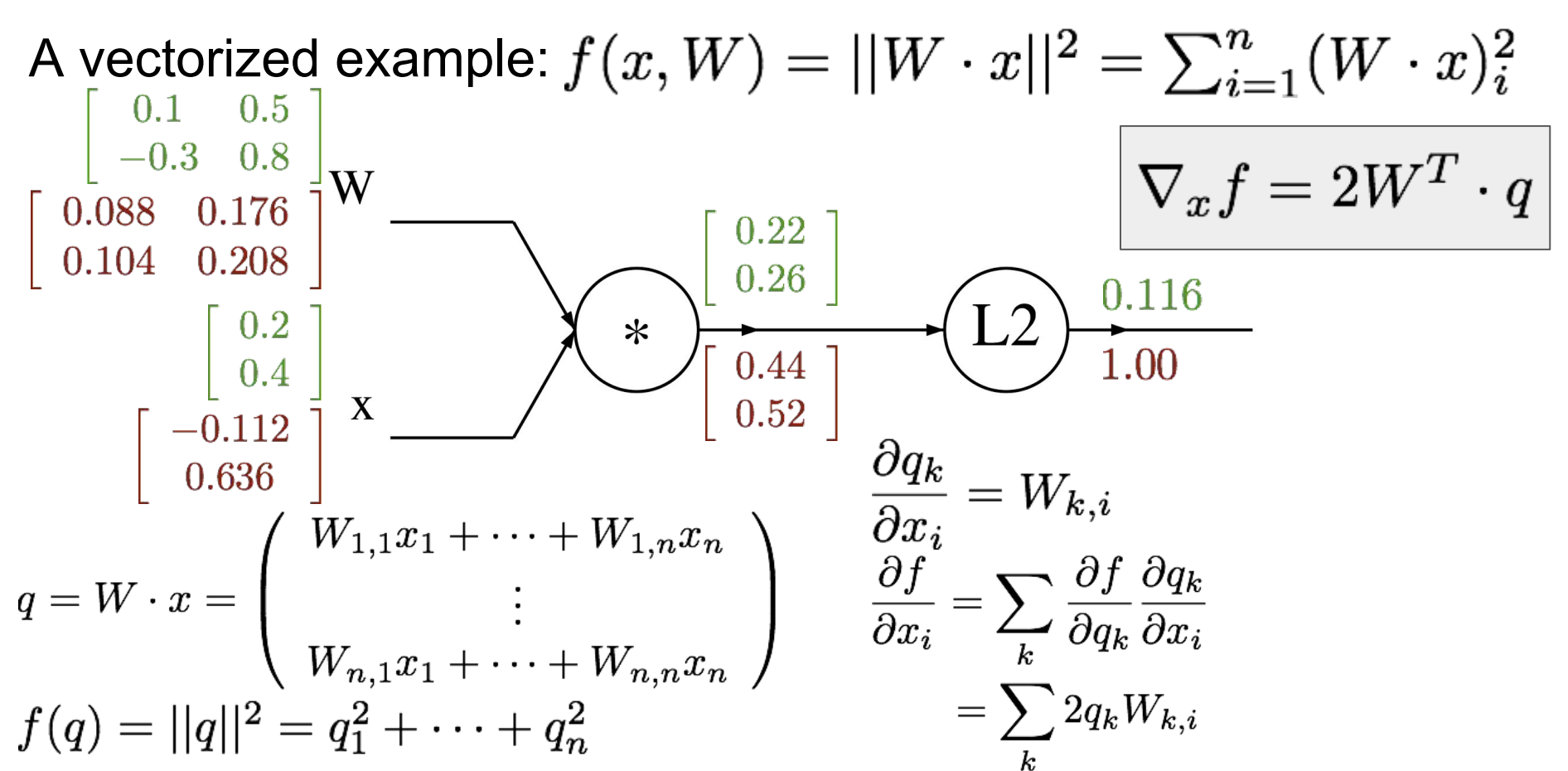
이렇게 결과적으로 구할 수 있고, 과제 1에서 SVM/ Softmax 통해 forward/ backward 를 직접 할 수 있다.
Neural Network
지금까지 선형 점수 함수에 대해서만 알아보았다면 이제는 2-layer Neural Network에 대해 알아볼 것이다.

여기서 h는 각 클래스의 점수값 벡터들을 의미하고, w2를 통해 s는 가중치를 부여하고 계산한 최종 점수를 의미한다.
과제 2에서는 2-layer에 대해 계산을 해보도록 하자.
여기서 사용하는 Neural 은 신경망이라는 의미이다.
우리 뇌 세포의 신경을 비유적으로 표현한 것이다.
하지만 진짜 생물학적인 신경에 가깝다는 의미는 아니다. 아주 느슨한 비유를 의미한다.
신경은 매우 다양한 타입들이 있고, dendrite에 해당하는 (ai에서는 input을 의미) 것은 아주 복잡한 비 선형 계산을 수행한다.
우리가 배우는 신경망 네트워크의 구조는 다음과 같다.
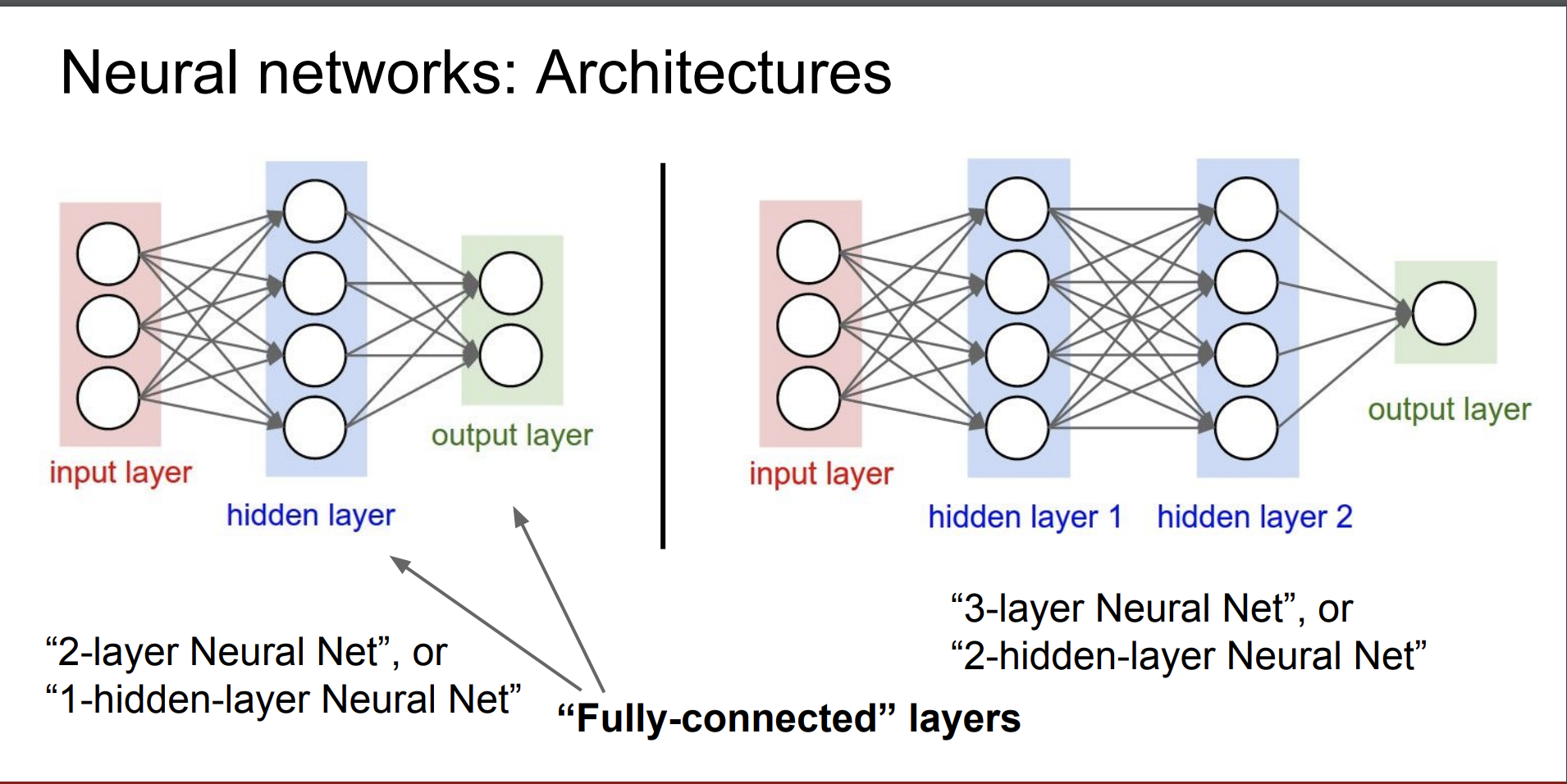
우리는 모든 층의 뉴런들을 활성화 함수를 통해 효율적으로 계산할 수 있다.

요약하면
- 완전 연결된 (fully-connected) 뉴런들로 배열한다.
- 층들은 벡터화 된 코드(행렬)을 통해 계산할 수 있다.
4강 끝 😆
