Lecture 1 Review

우선 강의 1은 완전 ot느낌이다.

컴퓨터비전의 역사와 앞으로 우리가 배울 내용을 다룬다.

그래도 간략하게 요약해보자.

Vision History

60년대 초반부터 컴퓨터비전의 역사가 시작된다.

• Larry Roberts, 1963
  기존 물건의 모양을 재구성하려 노력한다.

1970년대에는 객체를 단순한 기하학적 구성요소로 배치했다.

60~90년대에는 객체를 인식하려고 물건을 선 또는 모서리로 조합했으나 본질적 문제는 해결되지 않았다.

90년대에 들어서는 컴퓨터의 발전, 카메라의 발전으로 컴퓨터비전 역시 발전하게 되었다.

테스트세트를 활용하여 Visual Object Challenge를 하게 되었다.

대표적으로

-IMGENET large Sacle Visual Recognition Challenge이다.

그림에 대해 5개의 상위 라벨을 출력하고 해당 5개의 라벨에서 올바른 개체가 포함되었다면 성공한 것이다.

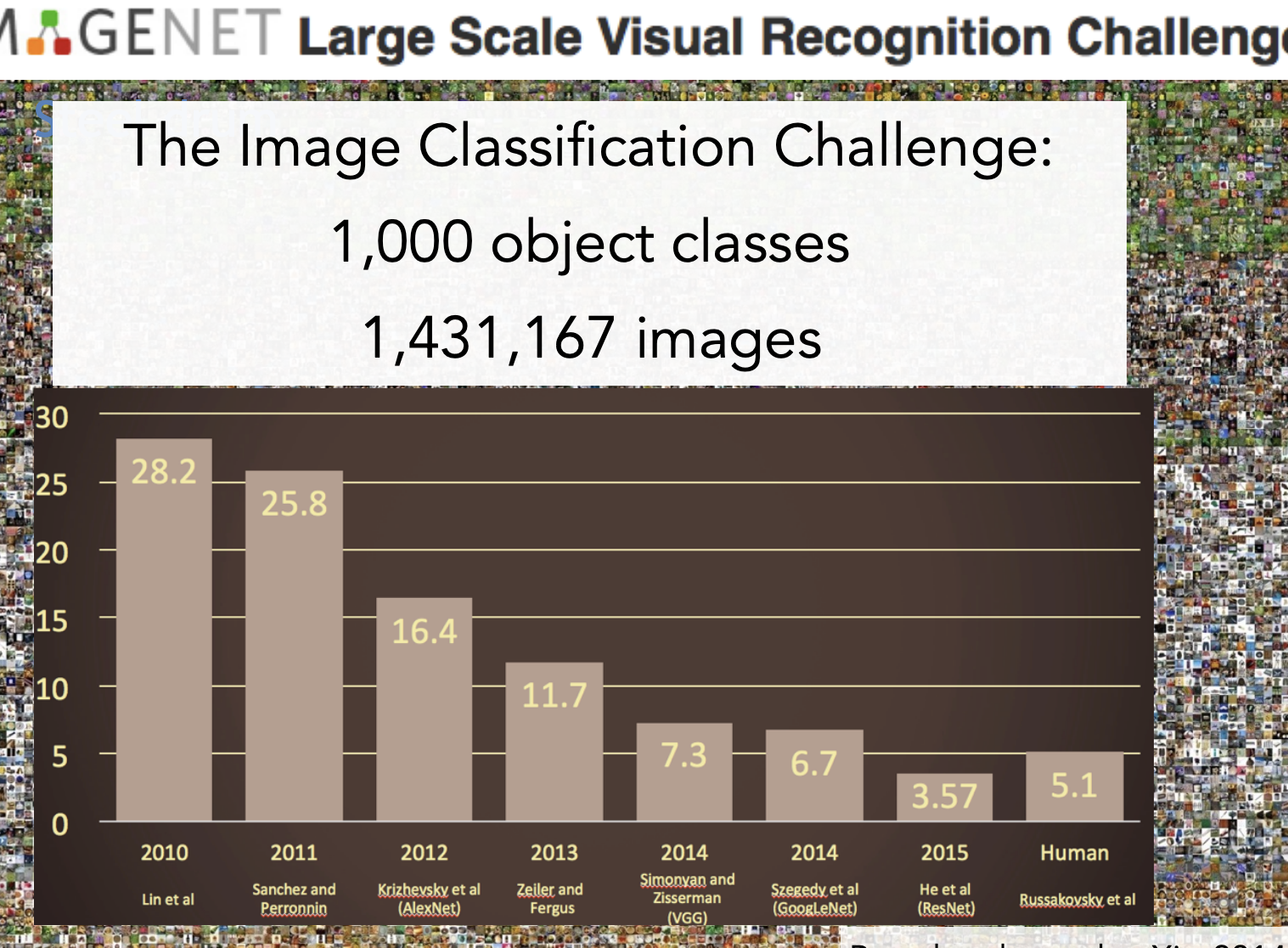
오류율이 시간이 갈수록 감소함을 알 수 있다.
2012년이 가장 감소율이 큰데, 2012년부터 CNN이 사용되었기 때문이다.

Overview

대략 이 수업은 이미지분류 문제를 다룬다.

이미지 분류 문제는

• Object detection
• Action classification
• Image captioning
  등등의 문제가 있다.

앞 서 역사에서 알 수 있듯 CNN은 객체 인식 문제에 가장 중요한 도구가 되었다.

하지만 CNN은 한순간에 개발된 것이 아니다.

• 계산기의 발달
• 더 많은 데이터 세트

로 인해 개발될 수 있었다.

으로 요약을 마무리하자...

Lecture 2

강의 2링크

이미지 분류

컴퓨터 비전에서 core work이라 말할 수 있다.

사진을 보고 cat인지 dog인지 .. 분류하는 것이다.

우리가 사진으로 보면 바로 인식이 가능하겠지만, 컴퓨터는 사진을 숫자로 인식한다.

이미지 분류에는 여러 Challenges가 있다.

• 같은 사물을 다른 관점에서 볼 때
• 명암의 정도가 다를 때
• 고양이가 서있거나 앉아있거나 등등 형태가 다를 때
• 고양이가 얼굴만 보이거나 풀 숲에 가려져 있거나 아니면 꼬리만 보일때 즉 Occlusion
• 배경과 물체가 비슷할 때 Background Clutter
• 고양이가 나이 또는 색상으로 나뉠 때 Intraclass variation

이 모든 것을 고려하여 모든 물체에 적용하는 것은 매우 힘들고 어려운 기술이다.

우리는 Data-Driven Approach를 통해 해결하려 한다.

1. 이미지와 라벨의 데이터를 고르고
2. 머신러닝을 사용하여 분류기를 학습시킨다.
3. 새로운 사진에 대해서 분류기를 평가한다.

Nearest Neighbor

우리가 처음 배우는 분류기는 바로 인접한 이웃을 선택하는 것이다.
가장 원시적이고 성능이 안좋지만 가장 심플하다.

이런 분류기에서 우리는 두 함수를 이용한다.

• train 함수
  - 모든 데이터와 라벨을 기억한다.
  - model을 반환한다.
• predict 함수
  - 모델을 통해 가장 비슷한 이미지를 찾는다.
  

데이터셋의 예시로는 CIFAR10가 있다.

이는 10개의 클래스, 50,000개의 훈련 사진, 10,000개의 테스트 사진들이 있다.

그럼 유사한 사진을 어떤 근거로 찾는가?
L1 distance를 사용한다.

$d_1(I_1,I2) = \sum_p |I_1^p - I_2^p|$
즉 두 차이의 절대값을 구하는 것이다.

여기서의 train함수는 그저 값을 저장하는 용도에 불과하다.
predict에서 모든 데이터와 new data를 비교하여 차이의 절대값을 구한다.

만약 n개의 예시가 있다면,
train : O(1)
predict : O(N)
의 시간이 걸린다.

이는 굉장히 안좋다. 왜냐하면 우리는 test의 시간을 단축해야 실제 모델에서 사용시 편리하기 때문이다.

일단 가장 인접한 하나를 선택한 것을 그림으로 표현해보자.

이렇게 나타낼 수 있는데 하나의 지역(point)는 가장 인접한 점에 대해서 색깔로 표시된다.

하지만 이는 왼쪽 빨강, 파랑부분의 경계선을 보면 굉장히 노이즈가 있다는 것을 알 수 있고 초록 지역 가운데 노란지역을 통해 해결해야할 문제가 있음을 알 수 있다.

위는 k=1로 설정한 것이다.
k는 점의 개수를 의미하며 우리가 만약 가장 가까운 하나만 찾는 것이 아닌, k개의 점을 찾아 투표를 하게 된다면 어떨까?

K-Nearest Neighbors

이를 줄여서 KNN이라 한다.

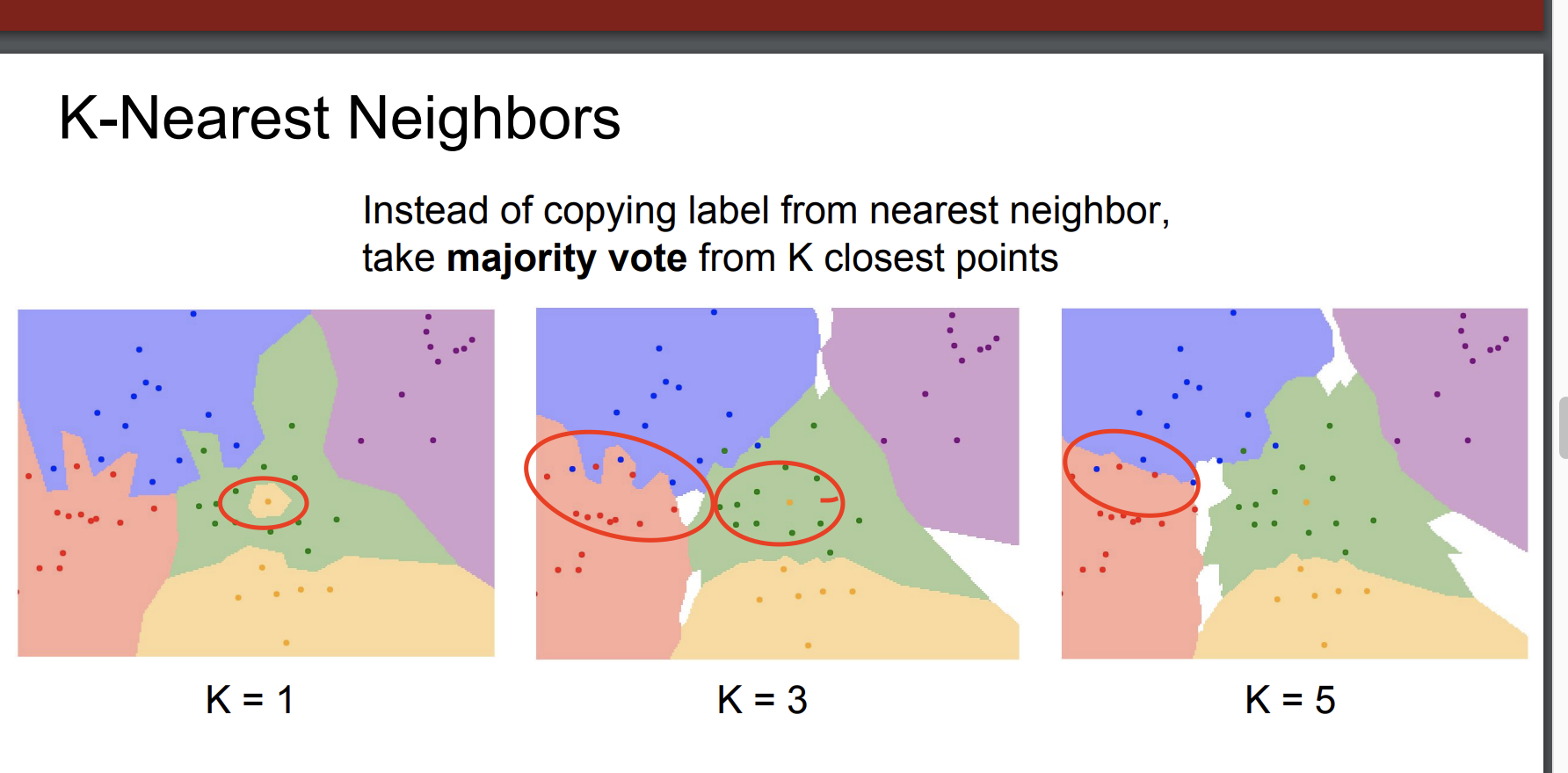
k가 많아질 수록 위에서 말한
노이즈, 오분류 문제가 사라진 것을 알 수 있다.

우리가 정한 L1말고 다른 계산법으로 거리를 구해보자.

L2(Euclidean) distance 라고 하며 이는
$d_2(I_1, I_2) = \sqrt{\sum_P(I_1^P - I_2^P)^2}$
라고 한다.

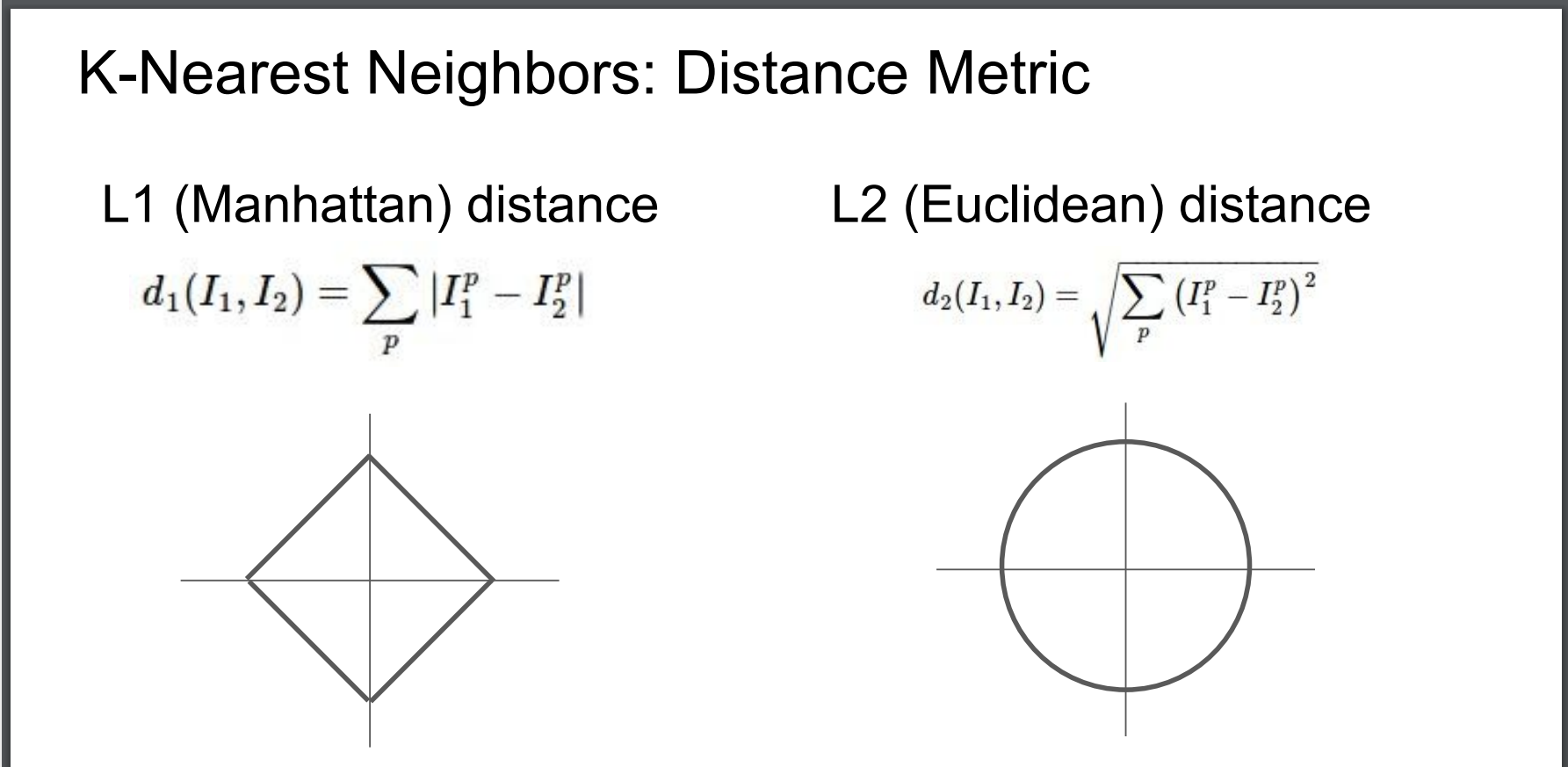
그리고 L1과 L2를 비교해보자.

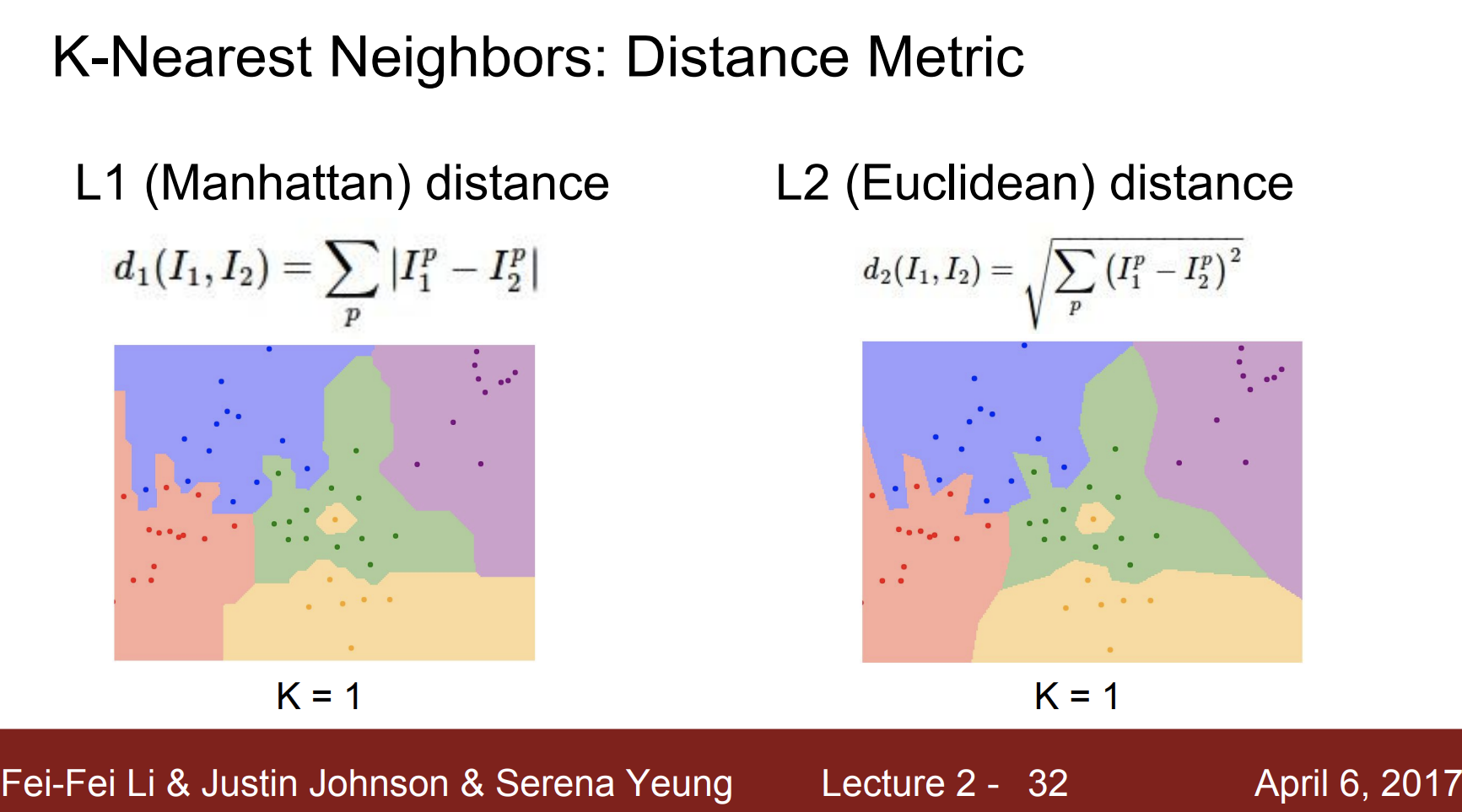
L2로 했을 때, 좀 더 자연스러운 경계를 그릴 수 있었다.

그 이유는 L1는 좌표축을 따르기 때문이다.

Hyperparameters

그럼 가장 최적의 k를 구할 수 있을까?
이를 hyperparameters라고 한다.
학습 전에 설정하는 선택같은 것이다.
모두 시험해 보고 가장 best인 것을 선택하는 것이 좋다.

그럼 hyperparameters들을 setting하는 방법은 뭐가 있을까?

idea 1. 데이터에 가장 좋은 초매개변수 선택

=> 이는 BAD 하다.
그 이유는?
훈련 데이터에 가장 best한 것은 과적합문제가 발생하기 때문이다.

idea2. 그럼 데이터를 train과 test로 나누자. 그리고 test data에 가장 좋은 초매개변수를 선택하자.

=> 역시 BAD
그 이유는?
새로운 데이터에 어떻게 반응할지 모른다.

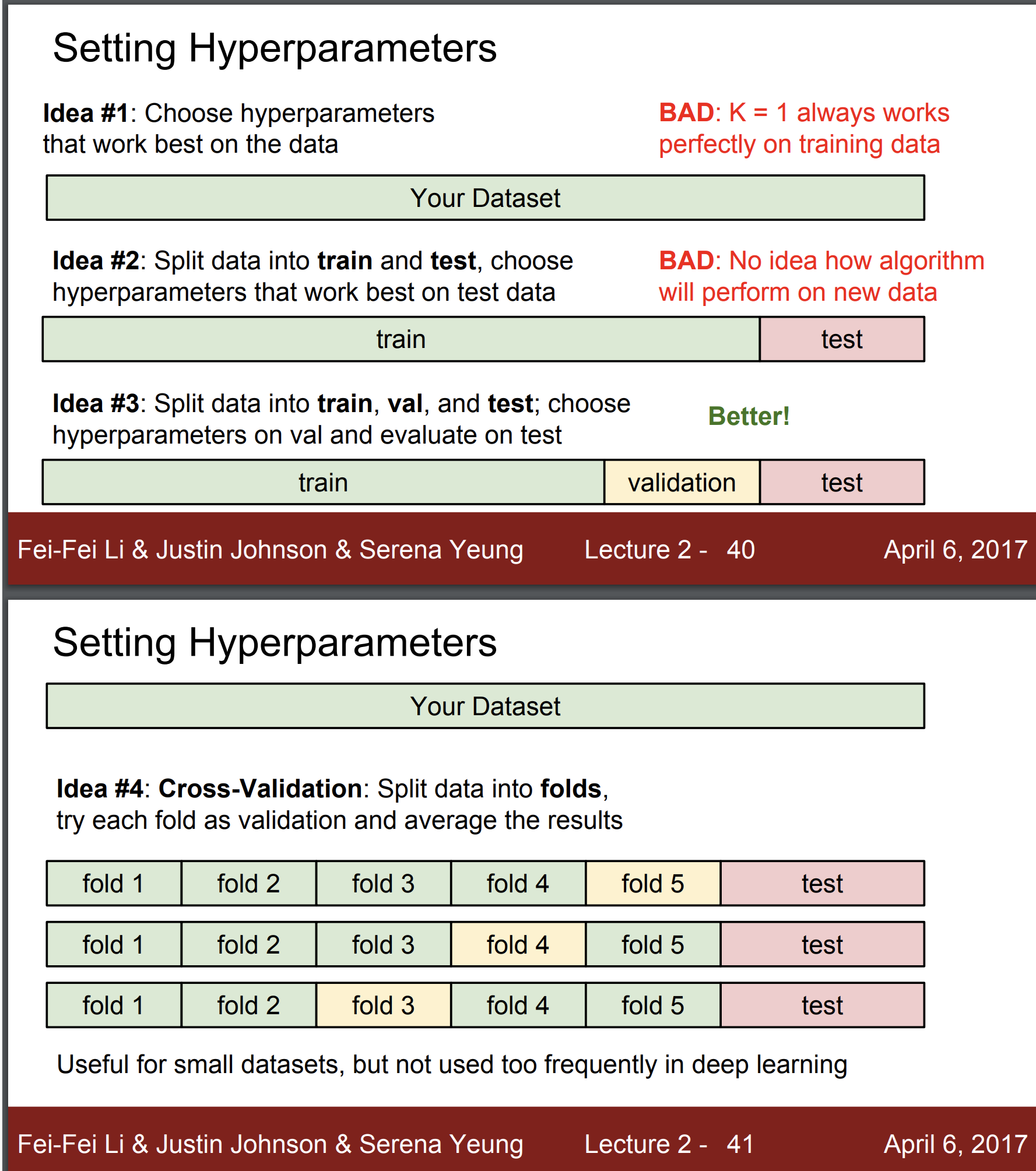
idea 3. 그럼 데이터를 train, validation, test로 나누자.

hyperparameters를 validation에서 선택한 다음 test에서 어떻게 반응하는지 확인하자.
=> GREAT!!

idea 4. Cross-Validation : folds로 나눈 다음에 여러번 test를 수행하자

=> small datasets에는 유용하나 데이터세트가 적은 경우엔 매우 expensive 하다.

그러나 KNN은 이미지 분류에 절대 사용되지 않는다.

그 이유는 test 시간이 너무 길고,
픽셀의 거리 측정 방식은 너무 정보량이 부족하기 때문이다.

같은 사진에 boxed, shifted, tinted된 사진들을 보면 모두 L2간의 거리가 같다. 하지만 모두 다 다른 사진임을 알 수 있다.

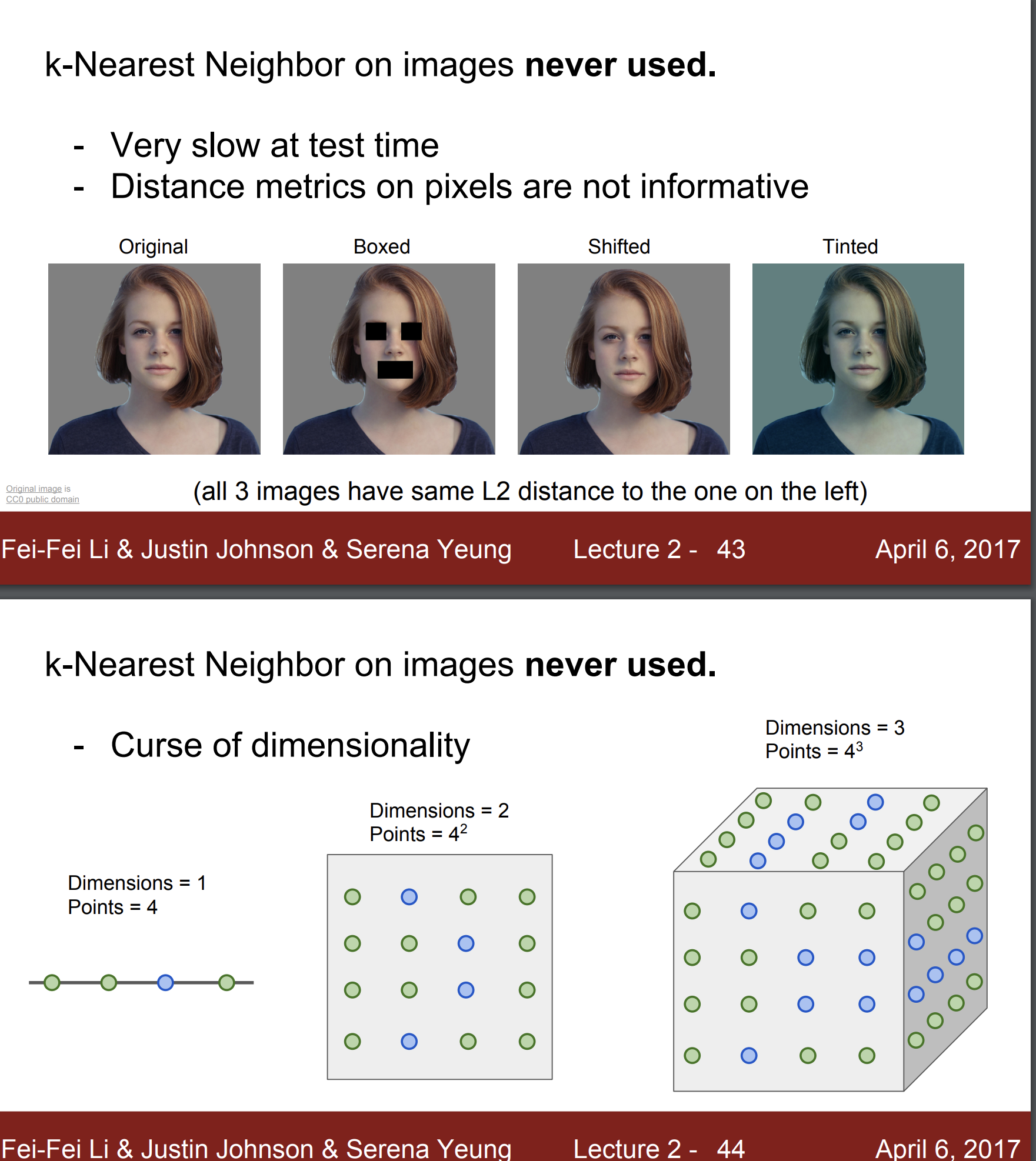
그리고 또한 차원의 저주 문제가 있다.

이는 차원이 커질수록 감당해야하는 데이터의 숫자가 기하학적으로 많아진다는 것이다.

Linear Classification

그래서 더 좋은 방법? 인 선형 분류법에 대해 알아보자.

선형 분류법이 레고 블럭처럼 쌓여서 Neural Network가 된다.
즉 우리는 선형 분류법에 대해 잘 알아야 나중에 배울 CNN에 대해서도 깊은 이해가 가능하다.

그럼 선형 분류법은 뭔가?
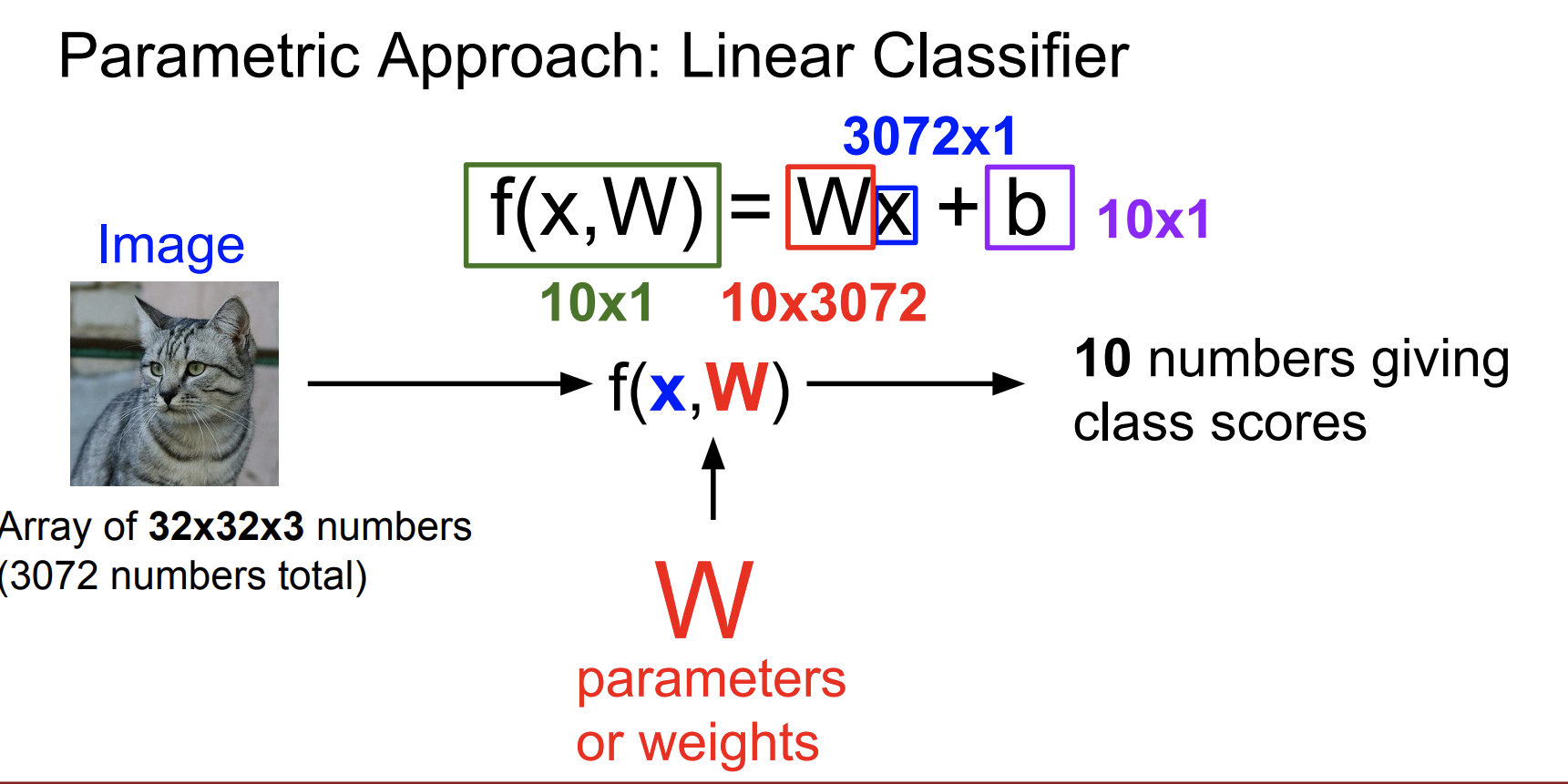
f(x,W)를 통해 분류한다.
그럼 f(x,W)가 뭔데..?

여기서 x는 우리가 입력으로 넣을 데이터를 의미하고
W는 parameters아니면 weight를 의미한다.

이전에 CIFAR10를 데이터 세트로 사용하자.
이미지를 넣고 해당 이미지의 10개의 클래스에 대한 점수를 출력하자.

우리가 만약 32x32 크기의 사진이 있다고 하자.
사진은 3원색이기 때문에 총 32x32x3 = 3072 가 크기가 된다.
우리는 10개의 숫자를 반환받아야 한다. (10x1)

input은 3072x1 가 된다. 그럼 W = (10, 3072)가 되어야 한다.

f(x,W) = Wx + b
b는 약간의 편향을 의미한다.
만약 데이터 셋에 데이터가 골고루 있다면 상관없으나 만약 개 보다 고양이의 사진이 훨 많다면 고양이로 분류할 확률이 더 높기 때문에 b에서 개의 점수를 좀 더 높일 수 있다.

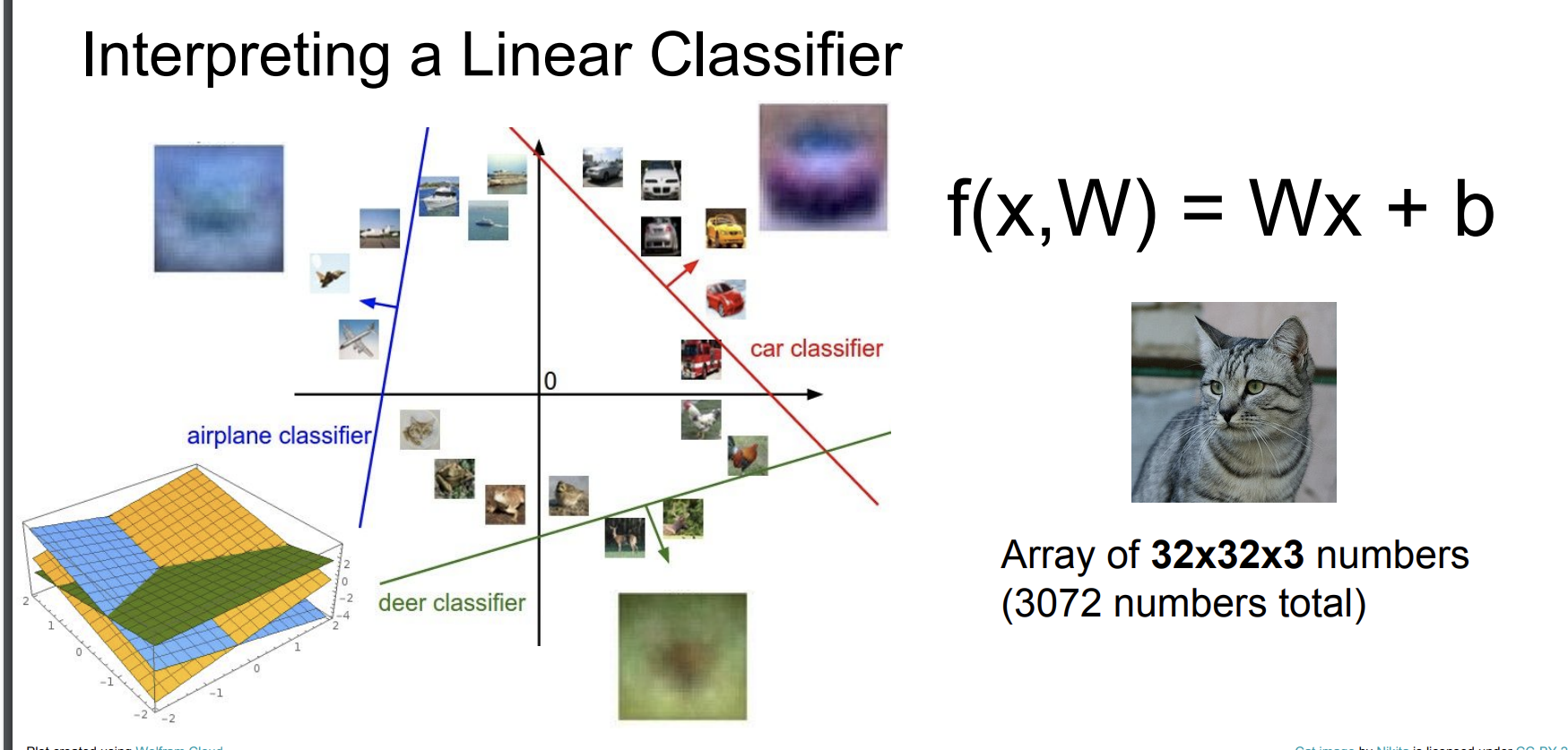
예를 들어 3개의 class로 나누는 예시를 보자.

4x4 픽셀을 예시로 들어서 W = (3 x 4)이고 x = (4 x 1) 그리고 편향 b는 (3x1) 이다.

W와 x는 서로 내적을 통해 곱해진다.

우리는 결과적으로 한 사진에 대해 여러 클래스의 점수를 얻게 된다.
이는 모든 사진에 대해 점수를 얻을 수 있고, 다시 말해 어떤 클래스에 대한 선형함수를 구할 수 있다.

즉 각 클래스에 대한 분류기를 구할 수 있다.

하지만 여러 문제점이 있다.

일단 선형 분류기는 class가 선형일 때만 정확하게 분리 가능하다.
또한 분리가 되어도 클래스에 따라 왼쪽 또는 오른쪽 둘 다에 속할 수 있다.

즉 아래와 같은 상황에 대해서는 정확하게 분류할 수 없다.

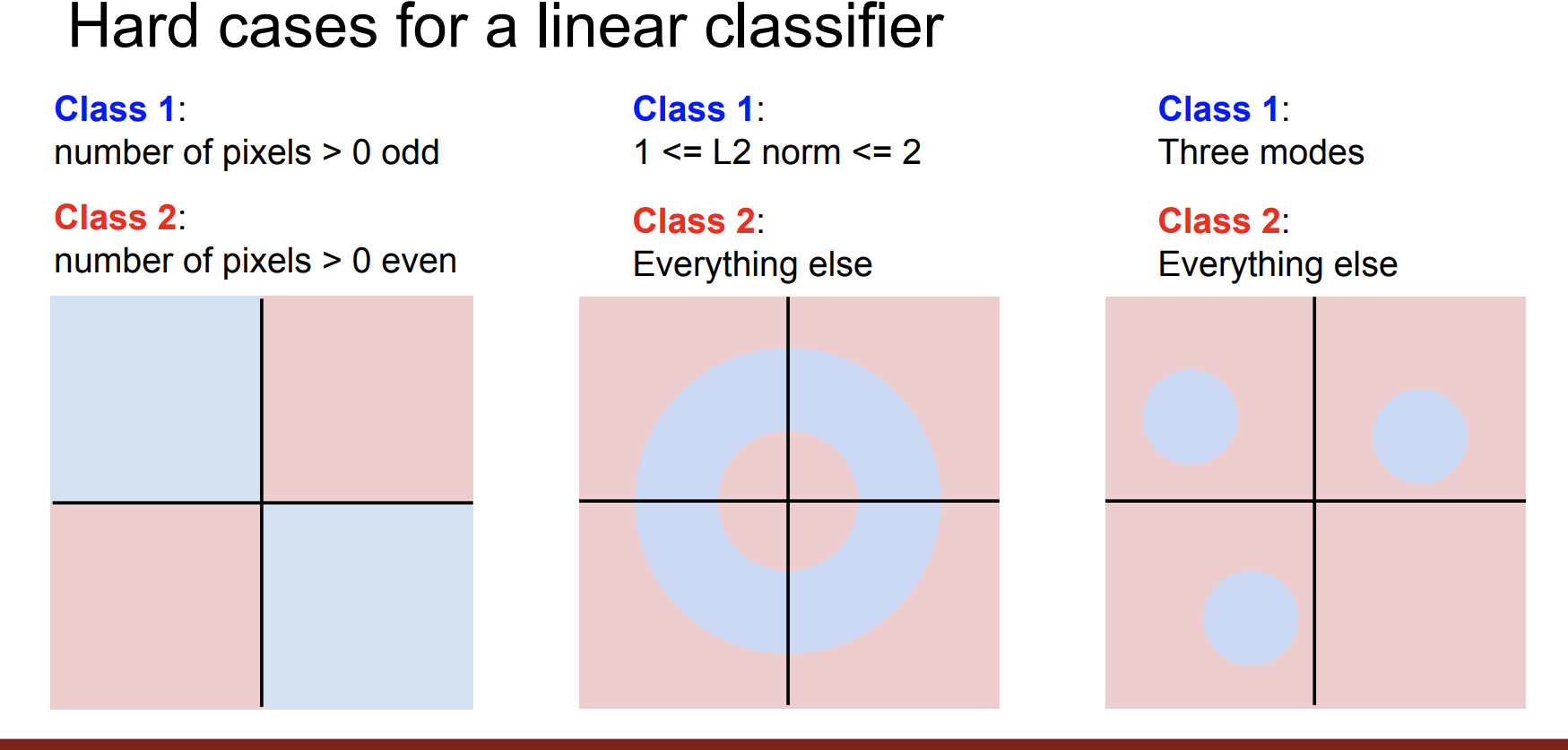
우리는 W에 대한 판단 또한 해야한다.

W가 과연 good or bad인지 확인해야한다.
이는 다음시간에 할 예정이다.