선형 회귀와 로지스틱 회귀

괴도소녀·2021년 7월 23일

Cross Entropy Gradient Descent Linear Regression Logistic Regression Regression multiclass logistic regression sigmoid softmax

Machine Learning

목록 보기

7/10

이번 포스팅에서는 선형회귀(Linear Regression)와 로지스틱 회귀(Logistic Regression)에 대해 알아보려 한다.

회귀(Regression)

회귀분석(Regression Analysis) 이란 통계학에서 전통적으로 많이 사용되던 분석 방법이다. 관찰된 여러 데이터를 기반으로 각 연속형 변수 간의 관계를 모델링하고 이에 대한 적합도를 측정하는 분석 방법이다.

예시를 들어보자면

미국의 집값
이산화탄소 배출량과 평균온도 상승률과의 관계 예측

예제의 문제들 모두

x: 독립변수(independent variable), 설명변수(explanatory variable)라고 불리기도 한다.
y: 종속변수(dependent variable), 반응변수(response variable)라고 불리기도 한다.

둘 사이의 상호 관련성을 설명하는 것이다.
선형 회귀분석은 간단하면서도 실생활에 적용되는 경우가 많기 때문에 선형 회귀분석의 기본 가정 내에 문제가 들어온다면 일단 먼저 회귀 분석을 시도해볼 만큼 문제를 해결할 때 많이 이용하게 되는 보편적인 방식이다.
선형회귀의 기본가정 4가지

지도학습(Supervised Learning)의 두 종류

분류(Classification)와 회귀(Regression)

분류 : 데이터 x의 여러 feature 값들을 이용하여 해당 데이터의 클래스 y를 추론하는 것
회귀 : 데이터 x의 여러 feature 값들을 이용하여 연관된 다른 데이터 y의 정확한 값을 추론하는 것

선형 회귀 분석(Linear Regression)

선형 회귀 분석은 회귀 분석을 대표하는 가장 대표적인 방법이며, 실생활에서 많이 접할 수 있는 문제들이다. 선형 회귀(linear regression)는 이름에서 알 수 있듯이, 종속변수 Y와 한 개 이상의 독립변수 X와의 선형 상관관계를 모델링하는 회귀분석 기법이다.
여기서 독립변수의 개수가 한 개의 독립변수를 가지고 있는 방식은 단순 선형회귀,
둘 이상의 독립변수를 가지고 있는 경우에는 다중 선형회귀라고 한다.

선형 회귀 모델링

선형 회귀의 식은 다음과 같다

y=βx+ϵ

밑에 둘은 데이터로부터 추정해야 하는 파라미터이다.

$β$ 는 회귀계수
$ϵ$ 는 종속 변수와 독립 변수 사이에 오차

$x$ 와 $y$ 에 해당하는 데이터가 있을 때 $\beta$ 와 $\epsilon$ 를 추정한 후,
추정한 값들을 바탕으로 모델링을 수행한다.

결국 선형회귀 모델을 찾는다는 것은 주어진 데이터에 선형 식이 잘 맞도록 회귀계수( $β$ ) 및 오차( $ϵ$ )를 구하는 것이라고 볼 수 있다.

머신러닝에서의 선형회귀모델 표기법

바로 위에서 선형회귀의 식을 보았으니 머신러닝에선 어떻게 표기하는지 알아보자

H=Wx+b

$H$ : 가정(Hypothesis)
$W$ : 가중치(Weight) <- $\beta$
$b$ 를 편향(bias) <- $ϵ$

머신러닝 혹은 딥러닝 기법을 이용해서 회귀 모델을 구한다는 얘기는, 주어진 데이터를 이용하여 이 $W$ 와 $b$ 를 구하기 위해서라는 뜻이다. 위 $W$ 와 $b$ 는 단순히 스칼라(scalr)값이 아닌 고차원 행렬(matrix)의 형태가 대부분이며, 파라미터 개수가 많아질수록 모델의 사이즈가 커지며 학습하는 난이도도 어려워진다.

용어

잔차(Residuals) 란 회귀모델을 이용해 추정한 값(predcit y)과 실제 데이터(original y)의 차이를 의미한다.

최소제곱법은 이 잔차를 이용하여 주어진 점 데이터들을 설명하는 회귀모델을 찾는 대표적인 방법 중 하나이며, 식은 다음과 같다.
$n$ 개의 점 데이터에 대하여 잔차의 제곱의 합을 최소로 하는 $W$ , $b$ 를 구하는 식이다.

argmin_{W,b}(\sum_{i=1}^n residuals^2)

회귀모델이 잘 결정되었는지 확인할 때 참고하는 지표로 결정계수(R-squared, 또는 R2 score 등으로 표기)라는 것이 있으며, 이는 0에서 1 사이의 값으로 나타나며, 1에 가까울수록 해당 회귀모델이 데이터를 잘 표현한다고 보면 된다.

경사 하강법(Gradient Descent Algorithm)

머신러닝에서는 가중치의 그래디언트(미분값)가 최소가 되는 지점이 손실함수를 최소로 하는 지점일 것이라는 가정을 한다. 왜냐하면 보통 가중치 함수는 아래로 볼록한 형태이기 때문이다.
그래디언트 값을 다음의 식으로 업데이트한다.

W:=W−α \begin{matrix} ∂ \over ∂W \end{matrix} J(W)

여기서 $α$ 에 해당하는 값이 learning rate이다. learning rate가 너무 크게 되면 최적의 $W$ 값을 건너뛰며 진행하는 경우가 생겨서 수렴하지 못하는 경우도 생기기 때문에 적절한 learning rate를 선정하는 것이 머신러닝,딥러닝에서는 굉장히 중요하다.

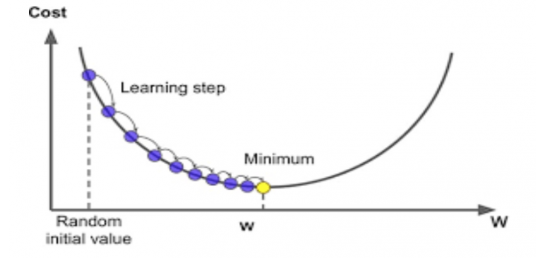
출처: https://bioinformaticsandme.tistory.com/125

로지스틱 회귀분석(Logistic Regression)

로지스틱 회귀분석(Logistic Regression) 이란 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고, 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해 주는 지도 학습(Supervised Learning) 알고리즘이다.

1개 이상의 독립변수가 있을 때, 데이터가 2개의 범주 중 하나에 속하도록 결정하는 이진 분류(binary classification) 문제를 풀 때 로지스틱 회귀분석을 많이 사용한다.

정의 및 용어 설명

로지스틱 회귀식은 다음과 같이 나타낸다.

LogOdds=log( \begin{matrix} P(y=0∣x) \over 1−P(y=0∣x) \end{matrix} )= β_0+ \sum_{j=1}^pβ_jx_ j

$Odds$ 는 사건이 발생할 확률을 발생하지 않을 확률로 나눈 값이다.
유방암 데이터셋에 맞추어 설명하자면, 악성 종양일 확률이 0.2라면 양성 종양일 확률은 자동적으로 0.8이 되니까 다음과 같이 $Odds$ 를 계산할 수 있다.

Odds(Malignant)= \begin{matrix} P(Y=0∣x) \over P(Y=1∣x) \end{matrix} = \begin{matrix} P(Y=0∣x) \over 1−P(Y=0∣x) \end{matrix} = \begin{matrix} 0.2 \over 0.8 \end{matrix} = 0.25

위 값에 log를 취한 값을 $Log-odds$ 라고 부른다.

log(0.25) = β_0+ \sum_{j=1}^pβ_jx_ j

$log-odds$ 의 식을 $P(Y=0|x)$ 에 대해서 다시 정리하게 되면,

P(y=0∣x)= \begin{matrix} exp(β_0+ \sum_{j=1}^p β_jx_j) \over 1+exp(β _0+ \sum_{j=1}^pβ_jx_j) \end{matrix}

위 식에서 $z = exp(β_0+ \sum_{j=1}^p β_jx_j)$ 로 치환하면, 아래와 같이 식이 간소해진다.

P(y=0∣x)= \begin{matrix} 1 \over 1+exp(-z) \end{matrix}

sigmoid function의 형태이다.

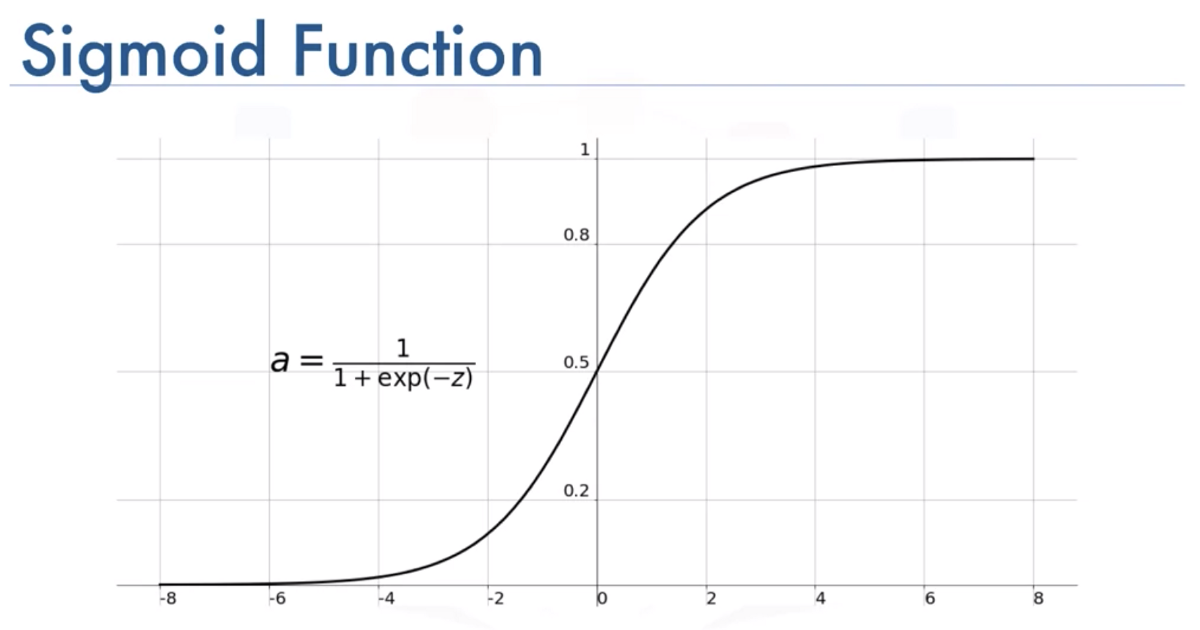
출처 : https://medium.com/@toprak.mhmt/activation-functions-for-deep-learning-13d8b9b20e

이쯤 되면 혼란스러울 것이다.
로지스틱 회귀는 과연 회귀 모델일까, 아니면 분류 모델일까? 로지스틱 회귀의 이름은 분명 이름인데 방금 유방암 분류 모델은 '분류'문제이다. 로지스틱 회귀는 '회귀' 모델이 맞으며, 모델이 리턴하는 값이 연속적인 변수라는 점에서 로지스틱 회귀는 회귀 모델의 정의에 부합한다. 단지, 우리가 이전 스텝에서 보았던 선형 회귀모델이 종속변수 $y$ 의 추정치 자체를 리턴하는 것에 비해, 로지스틱 회귀모델은 모델이 리턴하는 값이 바로 데이터 $x$ 가 어떤 범주에 속할 확률이라는 점이 다를뿐이다.

Softmax function, Cross Entropy

Softmax function

로지스틱 회귀(logistric regression)는 이진 분류뿐 아니라 여러 범주로 분류하는 다중 로지스틱 회귀(Multinomial Logistic Regression)으로 확장될 수 있으며, 시그모이드 함수는 다음과 같이 여러 범주로 분류하는 softmax 함수로 확장된다.

Softmax 함수는 여러 범주로(2가지가 아닌) 분류하는 함수이다. Multi class classification에 적합한 함수이다.

각 범주의 확률 값이 0에서 1 사이의 값이고, 또 하나의 큰 특징은 모든 범주에 해당하는 softmax의 값을 전부 더했을 때 그 합이 1이 된다. softmax 함수에 모든 범주의 log-odds를 통과시키면 해당 데이터가 어떤 범주로 분류되는지 확실히 알수있다. 가장 큰 값을 1, 그 외 나머지 값들을 0으로 인코딩하는 one-hot encoding을 통해 표현한다.

softmax(x)= \begin{matrix} e^{x_i} \over \sum_{j=0}^k e^{x_j} \end{matrix} (i=0,1,...k)

Cross Entropy

Cross entropy 함수는 위에서 살펴보았던 softmax 함수의 손실함수로 쓰인다.

H(p,q)=−x\sum p(x)\log q(x)

손실함수이기 때문에 가중치가 최적화될수록 $H(p,q)$ 의 값이 감소하게 되는 방향으로 가중치 학습이 되며,

$p(x)$ 는 실제 데이터의 범주 값
$q(x)$ 는 softmax의 결과값을 대입한다.

cross entropy를 쓰는 이유

정리 및 요약

	Linear Regression Analysis(선형회귀분석)	Logistic Regression Analysis(로지스틱 회귀분석)	Multiclass Logistic Regression(다중 로지스틱 회귀분석)
문제	종속변수가 연속형인 경우, 독립변수의 변화에 따른 종속변수 값의 추정	종속변수의 범주가 2개인 경우(2진 분류) 범주별 확률을 추정하여 최대확률 범주를 결정하는 분류모델로 활용	종속변수의 범주가 여러 개인 경우의 로지스틱 회귀분석
함수 및 변수	보편적으로 최소제곱법을 이용	logits(=log-odds), sigmoid 함수	cross entropy함수, softmax함수
손실함수	보편적으로 최소제곱법을 이용	cross entropy함수(대신 class가 2개)	cross entropy함수

괴도소녀

이전 포스트

학습데이터와 테스트 데이터 나누기

다음 포스트