5장. 오차역전파법 backpropagation - 1

괴도소녀·2021년 7월 27일

Backpropagation 오차역전파법

TFMaster

목록 보기

5/9

앞 포스팅에서의 수치미분은 단순하고 구현하기도 쉽지만 시간이 오래 걸린다는 것이 단점이다.
가중치 매개변수의 기울기를 효율적으로 계산하는 오차역전파법(backpropagation)을 이야기해보자.

이해하는 방법은 2가지가 있다.

수식을 통한 것
계산 그래프(computational graph) : 노드(node), 에지(edge)

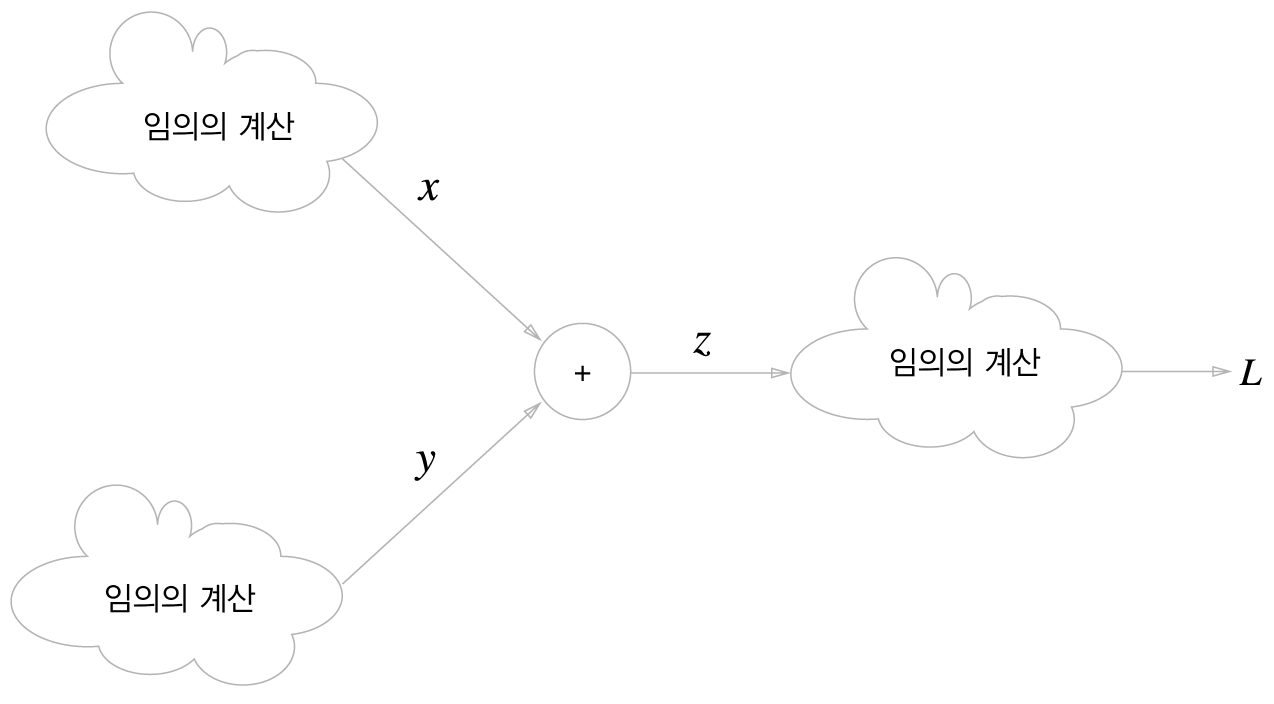
계산 그래프를 이용한 문제풀이는 다음과 같다.
1. 계산 그래프를 구성한다.
2. 그래프에서 계산을 왼쪽에서 오른쪽으로 진행한다.

계산을 왼쪽에서 오른쪽으로 진행하는 단계를 순전파(forward propagation)라고 한다. 이를 반대방향의 전파하는 것이 역전파(backward propagation)이다.

국소적 계산

계산 그래프의 특징은 '국소적 계산'을 전파함으로써 최종 결과를 얻는것이다.
국소적이란 '자신과 직접 관계된 작은 범위'라는 뜻이다.

비유를 해보자면 자동차 조립은 일반적으로 '조립 라인 작업'에 의한 분업으로 행해진다.
각 담당자는 단순화된 일만 수행하며, 그 일의 결과가 다음 담당자로 전달되어 최종적으로 차를 완성한다. 복잡한 계산을 '단순하고 극소적 계산'으로 분할하고 조립 라인 작업을 수행하며 계산 결과를 다음 노드에 전달한다.

왜 계산그래프로 푸는가?

계산 그래프의 이점은 방금 설명한 '국소적 계산'이다. 전체가 아무리 복잡해도 각 노드에서는 단순한 계싼에 집중하여 문제를 단순화할 수 있다. 또 다른 이점은, 계산 그래프의 중간 계산 결과들을 저장할 수 있다는 점이다. 실제로 계산 그래프를 사용하는 가장 큰 이유는 역전파를 통해 '미분'을 효율적으로 계산할 수 있다.

연쇄 법칙 Chain rule

'국소적 미분'을 전달하는 원리는 연쇄법칙(Chain rule)에 따른 것이다.

계산 그래프의 역전파

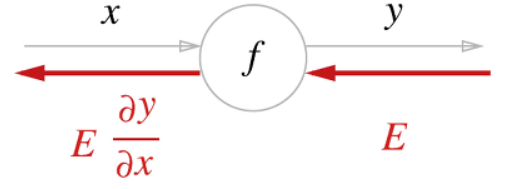
역전파의 계산 절차는 신호 $E$ 에 노드의 국소적 미분( $\partial y \over \partial x$ )을 곱한 후 다음 노드로 전달한다. 여기에서 말하는 국소적 미분은 순전파 때의 $y=f(x)$ 계싼의 미분을 구한다는 것이며, 이는 $x$ 에 대한 $y$ 의 미분 ( $\partial y \over \partial x$ )을 구한다는 뜻이다.

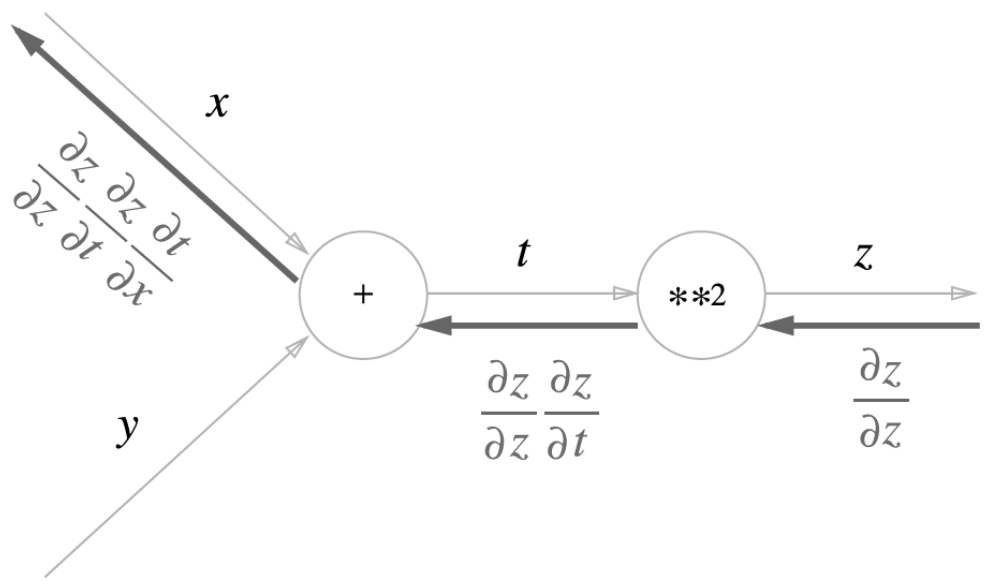
연쇄 법칙이란?

연쇄 법칙에 앞서 합성함수부터 설명해야한다. 합성 함수란 여러 함수로 구성된 함수이다.
예를 들어 $z=(x+y)^2$ 이란 식은 밑에 식처럼 구성된다.

z=t^2 \\ t = x + y

합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.

이것이 연쇄 법칙의 원리이다. 예를 들어 설명하자면 $\partial z \over \partial x$ ( $x$ 에 대한 $z$ 의 미분)은 $\partial z \over \partial t$ ( $t$ 에 대한 $z$ 의 미분)과 $\partial t \over \partial x$ ( $x$ 에 대한 $t$ 의 미분)의 곱으로 나타낼 수 있다.

\begin{matrix} \partial z \over \partial x \end{matrix} = \begin{matrix} \partial z \over \partial t \end{matrix} \begin{matrix} \partial t \over \partial x \end{matrix}

연쇄 법칙과 계산 그래프

위 그림과 같이 계산 그래프의 역전파는 오른쪽에서 왼쪽으로 신호를전파한다. 역전파의 계산 절차에서는 노드로 들어온 입력 신호에 그 노드의 국소적 미분(편미분)을 곱한 후 다음 노드로 전달한다.

역전파 backward propagation

첫번째로 덧셈 노드의 역전파를 해보겠다.
$z=x+y$ 라는 식을 대상으로 역전파를 살펴보겠다.

\begin{matrix} \partial z \over \partial x \end{matrix} = 1

\begin{matrix} \partial z \over \partial y \end{matrix} = 1

$\partial z \over \partial x$ 와 $\partial z \over \partial y$ 은 모두 1이 된다.

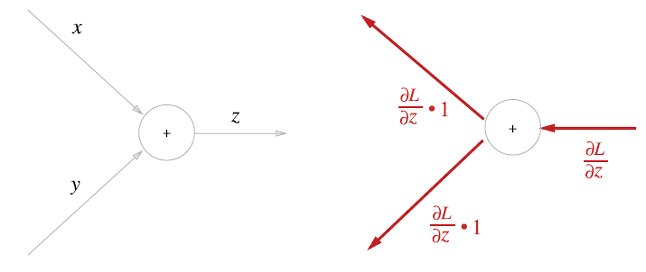
역전파 때는 상류에서 전해진 미분( $\partial L \over \partial z$ )에 1을 곱하여 하류로 흘린다. 즉, 덧셈 노드의 역전파를 1을 곱하기만 할 뿐이므로 입력된 값을 그대로 다음 노드로 보내게 된다.

곱셈 노드의 역전파

두번째로 곱셈 노드의 역전파를 살펴보자. $z=xy$ 라는 식으로 예를 들어보자.

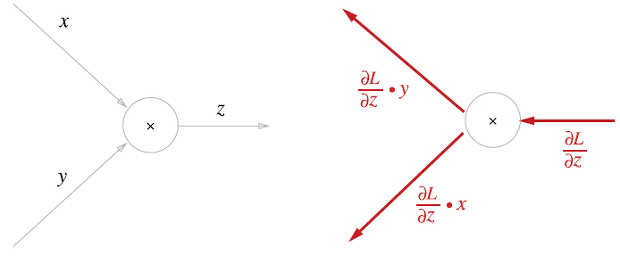
곱셈 노드의 역전파는 상류의 값에 순전파 때의 입력 신호들을 '서로 바꾼 값'을 곱해서 하류로 보낸다.

곱셈노드의 구체적인 예를 밑에와 같다.

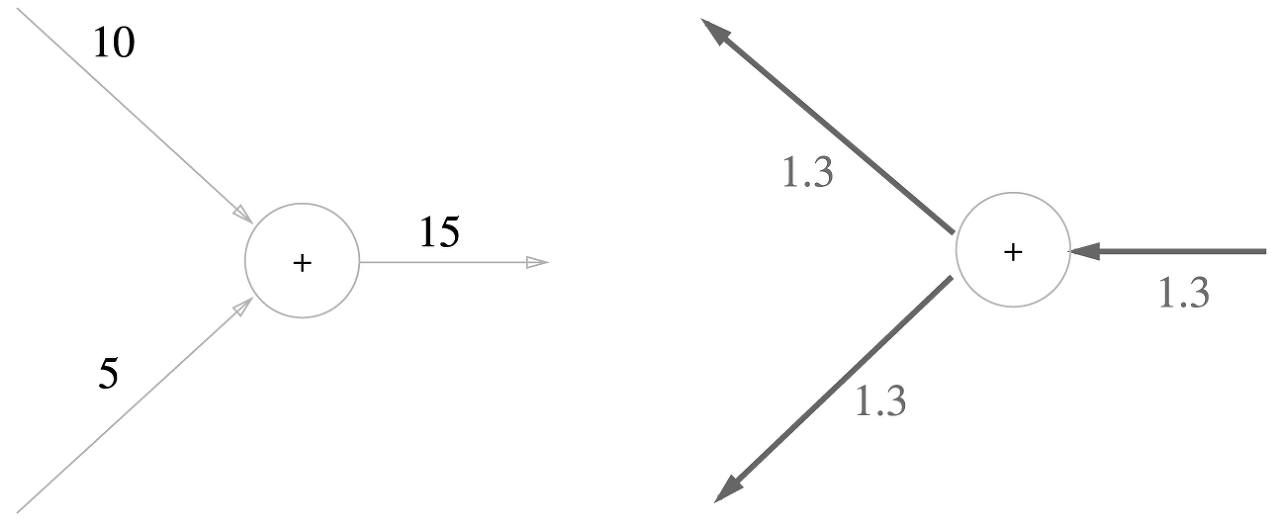
곱셈의 역전파에서는 입력 신호를 바꾼 값을 곱하여 하나는 1.3 x 5 = 6.5, 다른 하나는 1.3 x 10 = 13이 된다. 덧셈의 역전파에서는 상류의 값을 그대로 흘려보내서 순방향 입력 신호의 값이 필요하지 않았지만, 곱셈의 역전파는 순방향 입력 신호의 값이 필요하다. 그래서 곱셈 노드를 구현할 때는 순전파의 입력 신호를 변수에 저장해둔다.

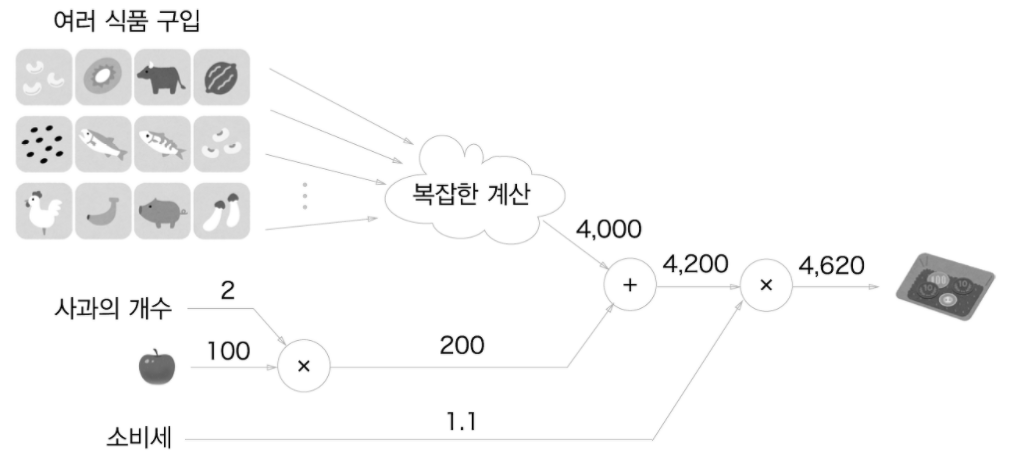
[사과쇼핑의 예]

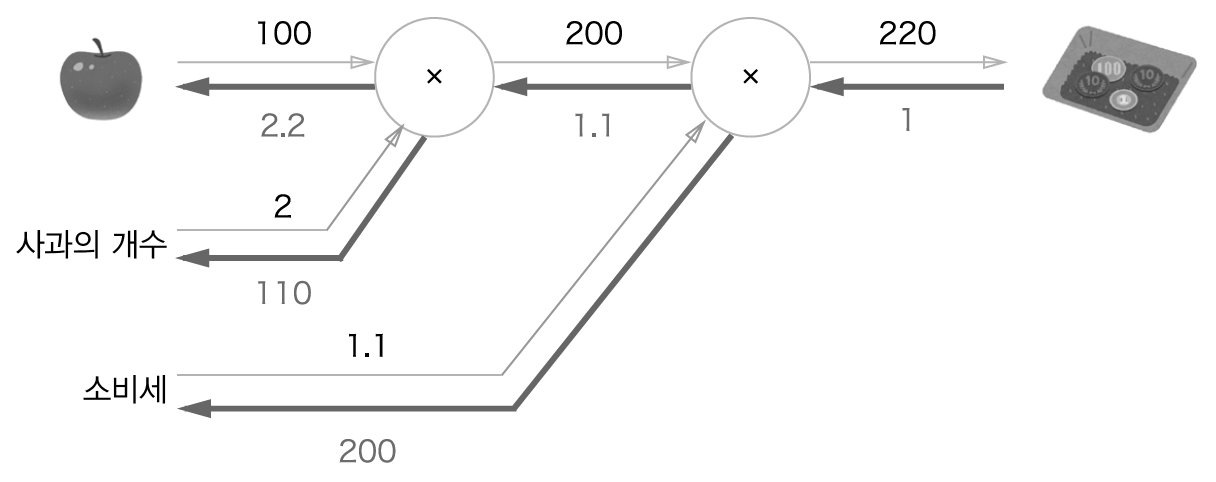
단순한 계층 구현하기

지금까지 예를 들었던 '사과 쇼핑'을 이용하여 파이썬으로 구현해보자.
그래프의 곱셈 노드를 'MulLayer', 덧셈 노드를 'AddLayer'라는 이름으로 구현한다.

# MulLayer 곱셈노드
class MulLayer: 
	def __init__(self): 
    	self.x = None 
    	self.y = None 
        
    def forward(self, x, y): 
    	self.x = x 
        self.y = y 
        out = x * y 
    
    def backward(self, dout): 
    	dx = dout * self.y # x와 y를 바꾼다.
        dy = dout * self.x 
        
        return dx, dy
 
# AddLayer 덧셈노드
class AddLayer: 
	def __init__(self): 
    	pass 
    
    def forward(self, x, y): 
    	out = x + y 
        return out 
        
    def backward(self, dout): 
    	dx = dout * 1 
        dy = dout * 1 
        
        return dx, dy

MulLayer를 사용하여 순전파를 다음과 같이 구현할 수 있다.

apple = 100 
apple_num = 2 
tax = 1.1 

#계층들 
mul_apple_layer = MulLayer() 
mul_tax_layer = MulLayer() 

#순전파 
apple_price = mul_apple_layer.forward(apple, apple_num) 
price = mul_tax_layer.forward(apple_price, tax) 

print(price) # 220

각 변수에 대한 미분은 backward()에서 구할 수 있다.

#역전파 
dprice = 1 
dapple_price, dtax = mul_tax_layer.backward(dprice) 
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print(dapple, dapple_num, dtax) # 2.2 110 200

backward()의 호출순서는 forward()때와는 반대이다.
backward()가 받는 인수는 '순전파의 출력에 대한 미분'임을 명심하자.

덧셈노드는 다른 똑같은 사과 쇼핑 예지이지만 조금 더 복잡한 그래프를 사용해보자.

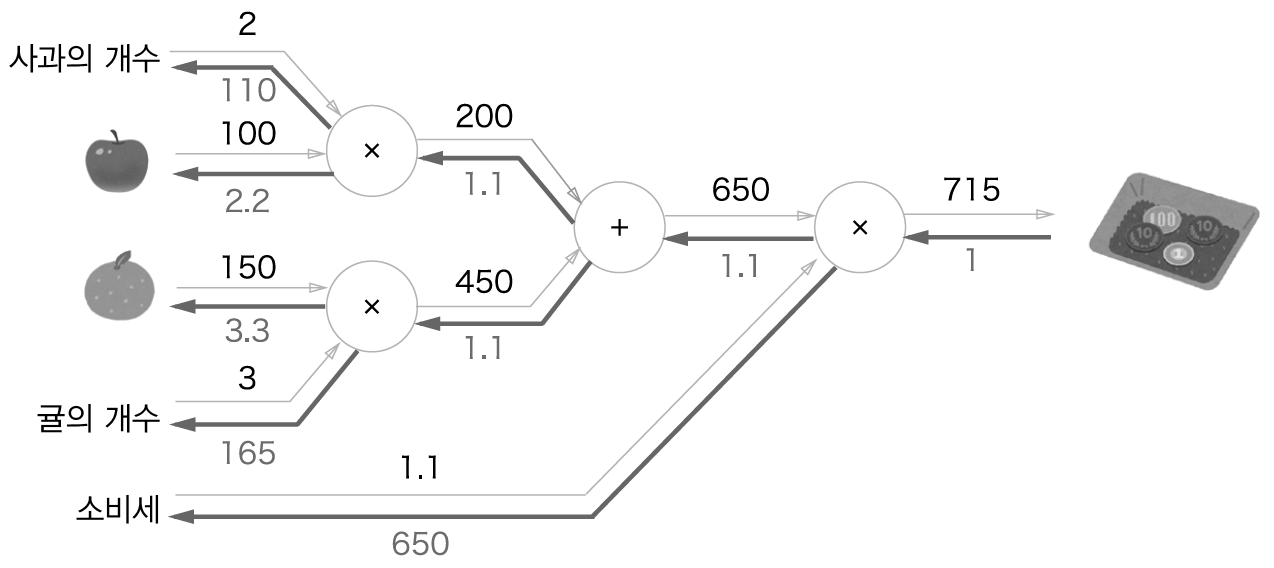
위의 그림을 이용하여 덧셈노드를 구현할 것이다.

# coding: utf-8 
from layer_naive import * 
apple = 100 
apple_num = 2 
orange = 150 
orange_num = 3 
tax = 1.1 

# layer 계층들
mul_apple_layer = MulLayer() 
mul_orange_layer = MulLayer() 
add_apple_orange_layer = AddLayer() 
mul_tax_layer = MulLayer() 

# forward 순전파
apple_price = mul_apple_layer.forward(apple, apple_num) # (1) 
orange_price = mul_orange_layer.forward(orange, orange_num) # (2) 
all_price = add_apple_orange_layer.forward(apple_price, orange_price) # (3) 
price = mul_tax_layer.forward(all_price, tax) # (4) 

# backward 역전파
dprice = 1 
dall_price, dtax = mul_tax_layer.backward(dprice) # (4) 
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price) # (3) 
dorange, dorange_num = mul_orange_layer.backward(dorange_price) # (2) 
dapple, dapple_num = mul_apple_layer.backward(dapple_price) # (1) 

print("price:", int(price)) print("dApple:", dapple) 
print("dApple_num:", int(dapple_num)) print("dOrange:", dorange) 
print("dOrange_num:", int(dorange_num)) print("dTax:", dtax)

필요한 계층을 만들어 순전파 메서드인 forward()를 적절한 순서로 호출한 다음, 역전파 메서드인 backward()를 호출하면 원하는 미분이 나온다.

활성화 함수 계층 구현하기

계산 그래프에 활성화 함수를 적용할 수 있다. 신경망을 구성하는 층(계층) 각각을 클래스 하나로 구현한다.

ReLU 계층

y = \begin{cases} x & {(x > 0) }\\ 0 & {(x \leq 0)} \end{cases}

$x$ 에 대한 $y$ 의 미분은 밑에와 같이 구해진다.

\begin{matrix} \partial y \over \partial x \end{matrix} = \begin{cases} 1 & {(x > 0) }\\ 0 & {(x \leq 0)} \end{cases}

순전파 때의 입력인 $x$ 가 0보다 크면 역전파는 상류의 값을 그대로 하류로 흘리며,
순전파 때 $x$ 가 0이하면 역전파 때는 하류로 신호를 보내지 않는다.

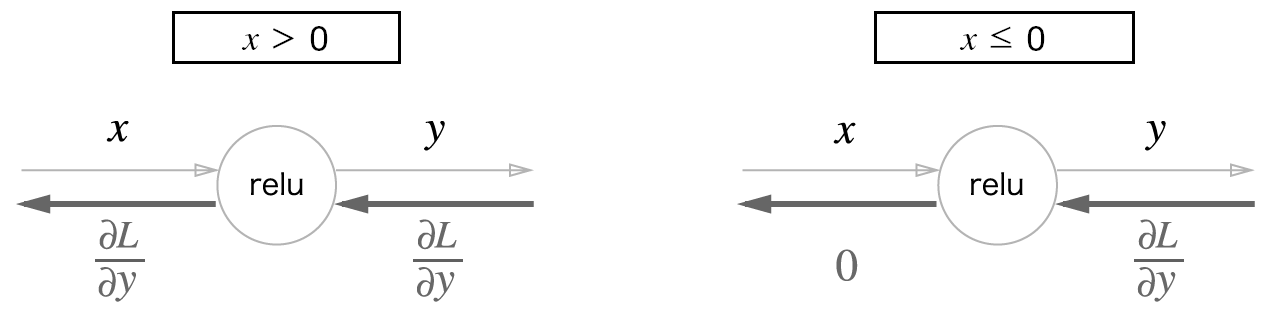
인제 ReLU 계층을 구현해보자. 이때 forward()와 backward()함수는 넘파이 배열을 인수로 받는다고 가정한다.

class Relu: 
	def __init__(self): 
    	self.mask = None 
        
    def forward(self, x): 
    	self.mask = (x <= 0) 
        out = x.copy() 
        out[self.mask] = 0 
        
        return out 
        
    def backward(self, dout): 
    	dout[self.mask] = 0 
        dx = dout 
        
        return dx

Relu 클래스는 mask라는 인스턴스 변수를 가진다.
mask는 True/False로 구성된 넘파이 배열로, 순전파의 입력인 x의 원소 값이 0 이하인 인덱스는 True, 그 외(0보다 큰 원소)는 False로 유지한다. mask 변수는 다음 예와 같이 True/False로 구성된 넘파이 배열을 유지한다.

>>> x = np.array([[1.0, -0.5], [-2.0, 3.0]]) 
>>> print(x) 
[[ 1. -0.5] 
[-2. 3. ]] 
>>> mask = (x <= 0) 
>>> print(mask) 
[[False True] 
[ True False]]

위의 그림과 같이, 순전파 때의 입력 값이 0 이하면 역전파 때의 값은 0이 되어야 한다. 그래서 역전파 때는 순전파 때 만들어둔 mask를 써서 mask의 원소가 True인 곳에서는 상류에서 전파된 dout을 0으로 설정한다.

Sigmoid 계층

시그모이드 함수의 식은 다음과 같다.

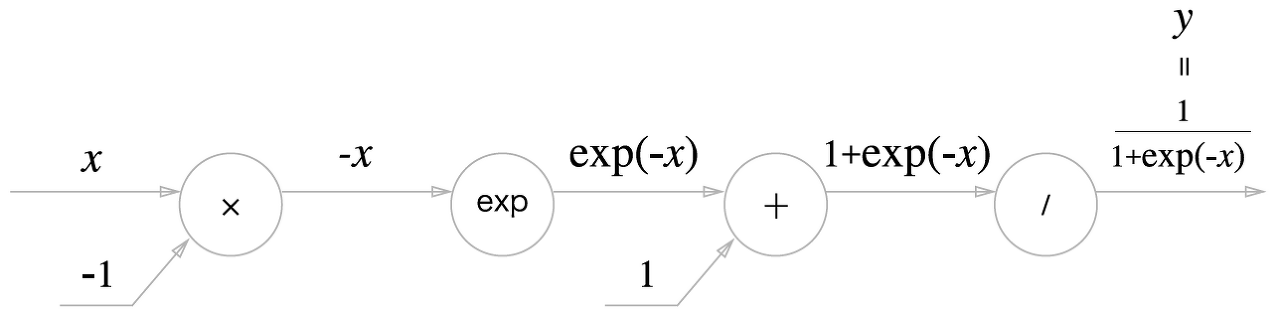
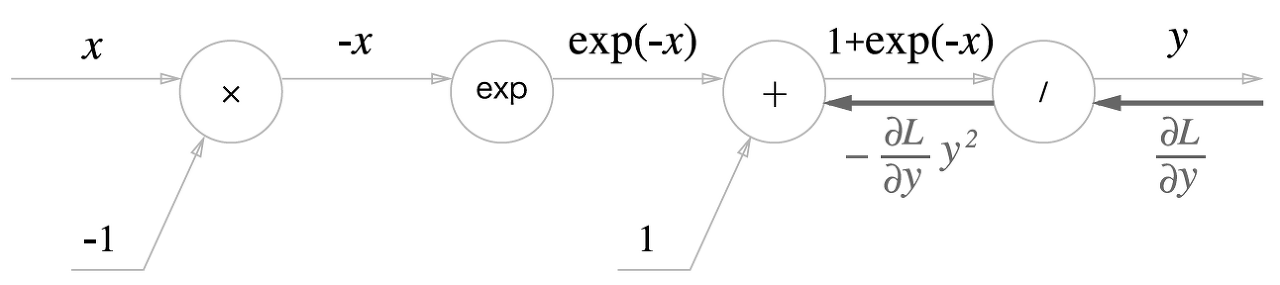
y = \begin{matrix} 1 \over {1 + \exp (-x)} \end{matrix}

'x'와 '+' 노드 말고도 'exp'와 '/' 노드가 새롭게 등장했다.
위 그림과 같이 시그모이드 함수 식의 계산은 국소적 계산의 전파로 이뤄진다. 이제 위 그림의 역전파를 하나씩 알아보자.

1단계

'/' 노드, 즉 $y = \begin{matrix} 1 \over x \end{matrix}$ 를 미분하면 다음 식이 된다.

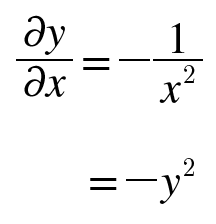
위의 식에 따르면 역전파 때는 상류에서 흘러온 값에 $-y^2$ 을 곱해서 하류로 전달한다.

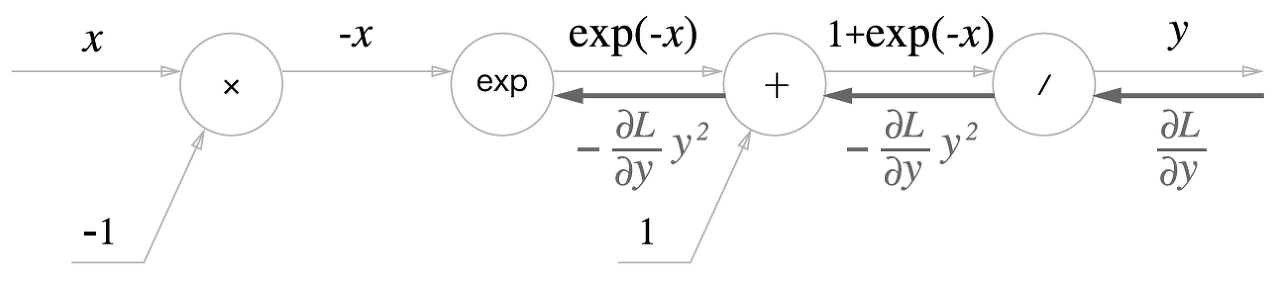
2단계

'+' 노드는 상류의 값을 여과 없이 하류로 내보내는 게 다이다.

3단계

'exp'노드는 $y = \exp (x)$ 연산을 수행하며, 그 미분은 다음과 같다.

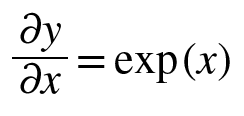
계산 그래프에서는 상류의 값에 순전파 때의 출력(이 예에서는 $\exp(-x)$ )을 곱해 하류로 전파한다.

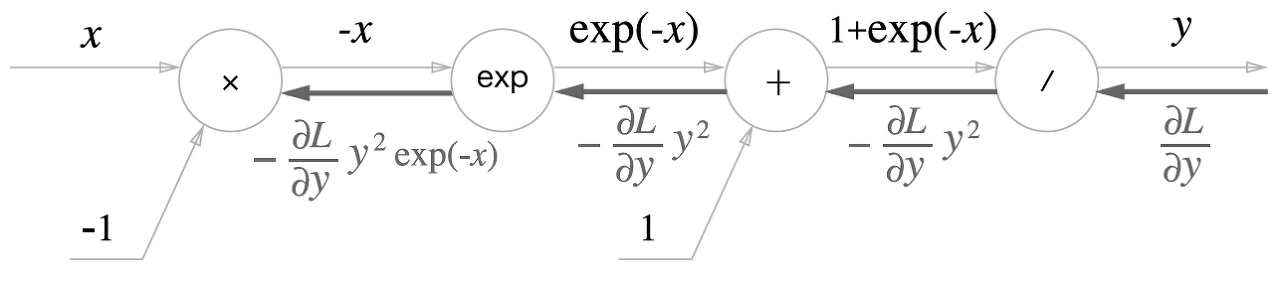
4단계

'x' 노드는 순전파 때의 값을 '서로 바꿔' 곱한다. 이 예에서는 -1을 곱하면 된다.

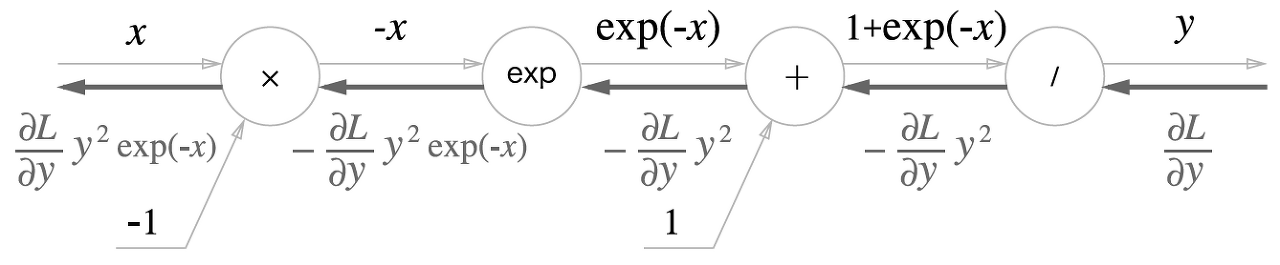
이상으로 계산 그래프를 완성했다. 이때, 시그모이드 함수의 역전파는 최종 결과물 $\begin{matrix}dL \over dy\end{matrix} y^2 \exp(-x)$ 로 묶을 수 있으므로, 다음과 같이 간단하게 표현할 수 있다.

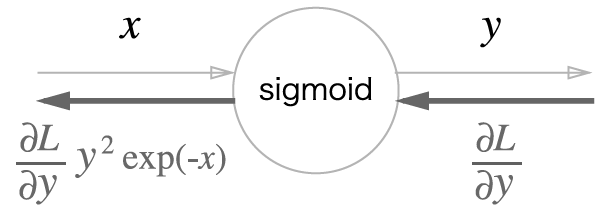
결과는 같으나, 노드의 그룹화를 통해 입력과 출력에 집중할 수 있다!

또한, $\begin{matrix}dL \over dy\end{matrix} y^2 \exp(-x)$ 은 다음처럼 정리해서 쓸 수 있다.

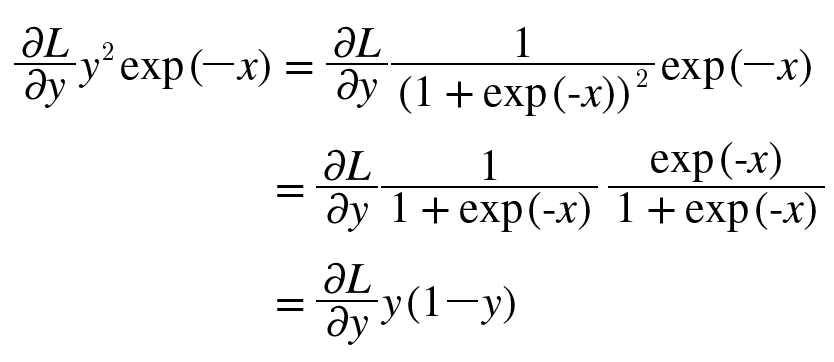
이처럼, Sigmoid 계층의 역전파는 순전파의 출력 (y) 만으로 계산할 수 있다.

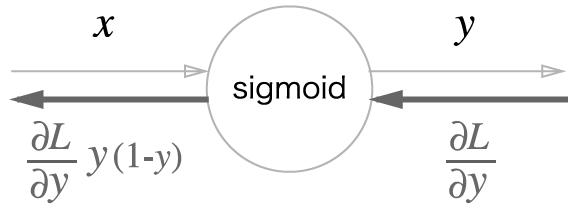
Sigmoid 계층을 파이썬으로 구현해보자.

class Sigmoid: 
	def __init__(self): 
    	self.out = None 
        
    def forward(self, x): 
    	out = sigmoid(x) 
        self.out = out 
        
        return out 
        
    def backward(self, dout): 
    	dx = dout * (1.0 - self.out) * self.out 
    
    	return dx

이 구현에서는 순전파의 출력을 인스턴스 변수 out에 보관했다가, 역전파 계산 때 그 값을 사용한다.

Affine/Softmax 계층 구현하기

Affine 계층

신경망의 순전파에서는 가중치 신호의 총합을 계산하기 때문에 행렬의 곱(넘파이에서는 np.dot())을 사용했다. 예시 코드는 아래와 같다.

X = np.random.rand(2) # 입력
W = np.random.rand(2,3) # 가중치
B = np.random.rand(3) # 편향

X.shape # (2,) 
W.shape # (2,3) 
B.shape # (3,) 

Y = np.dot(X.W) + B

위 코드를 그래프로 표현하면 아래와 같다.

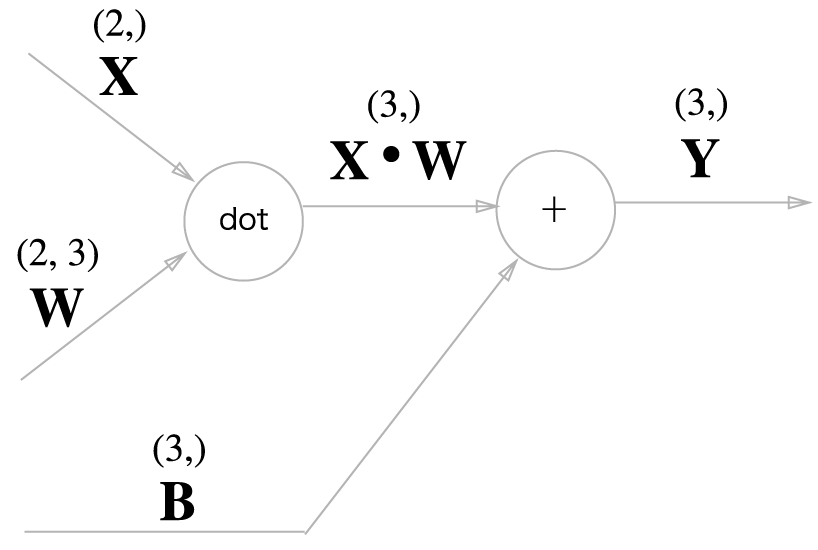
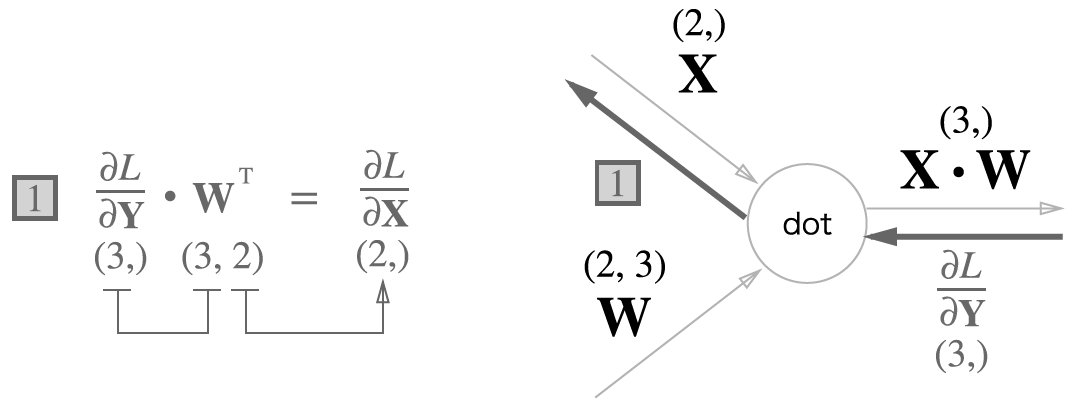
이제 위 그래프의 역전파에 대해 생각해보자. 행렬을 사용한 역전파도 행렬의 원소마다 전개해보면 스칼라값을 사용한 지금까지의 계산 그래프와 같은 순서로 생각할 수 있다.

\begin{matrix} \partial L \over \partial X \end{matrix} = \begin{matrix} \partial L \over \partial Y \end{matrix} \cdot W^T

\begin{matrix} \partial L \over \partial W \end{matrix} = X^T \cdot \begin{matrix} \partial L \over \partial Y \end{matrix}

$W^T$ 는 $W$ 의 전치 행렬을 뜻한다. 전치행렬은 ( $i$ , $j$ )위치의 원소를 ( $j$ , $i$ )위치를 바꾼 것을 말한다.

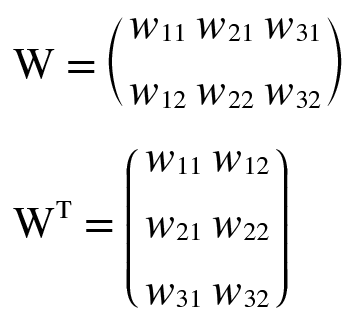
위 식을 바탕으로 계산 그래프의 역전파는 아래 그림과 같이 나타낼 수 있다.

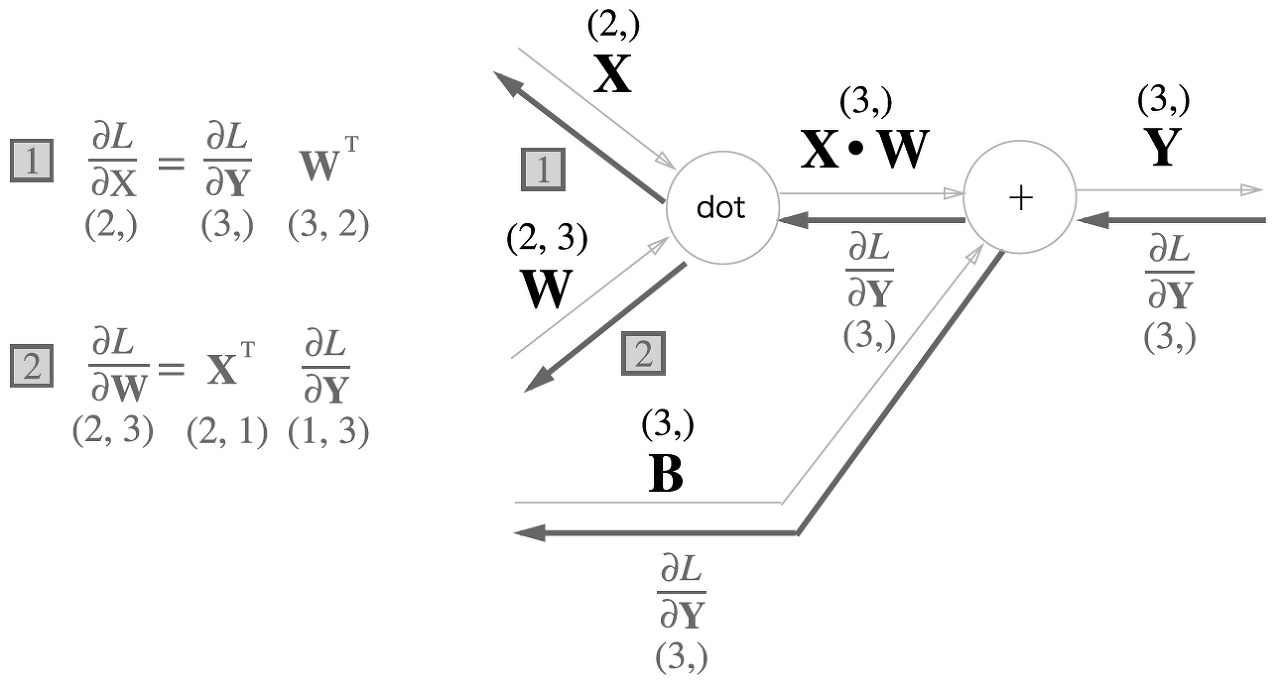
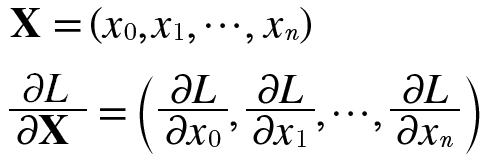
계산 그래프에서 각 변수의 형상에 주의해야한다. 특히 $X$ 와 $\partial L \over \partial X$ 은 같은 형상이며, $W$ 와 $\partial L \over \partial W$ 도 같은 형상이다.

이때, 행렬 곱의 역전파는 행렬의 대응하는 차원의 원소 수가 일치하도록 잘 조립해주어야 한다.

배치용 Affine 계층

지금까지의 Affine 계층은 입력 데이터로 X 하나만을 고려한 것이었다. 이번 절에서는 데이터 N개를 묶어 순전파하는 경우, 즉 배치용(데이터 묶음) Affine 계층을 생각해 보자.

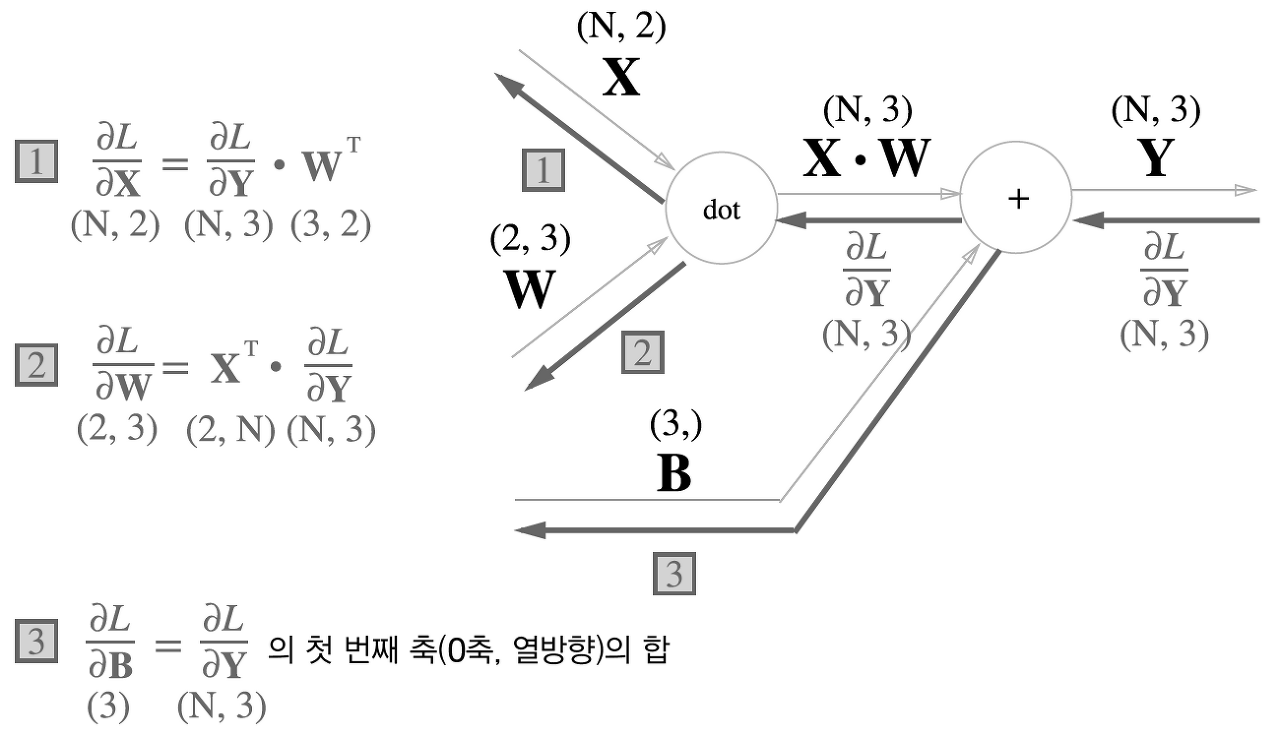
기존과 다른 부분은 입력인 X의 형상이 (N, 2)가 된 것뿐이다. 그 뒤로는 지금까지와 같이 계산 그래프의 순서를 따라 순순히 행렬 계산을 하게 된다.

편향을 더할 때도 주의해야 한다. 순전파 때의 편향 덧셈은 $X \cdot W$ 에 대한 편향이 각 데이터에 더해진다. 예를 들어 N = 2(묶음이 2개짜리)로 한 경우, 편향은 그 두 데이터 각각에(각각의 계산 결과에) 더해진다. 코드를 한번 보자.

>>> X_dot_W = np.array([[0, 0, 0], [10, 10, 10]]) 
>>> B = np.array([1, 2, 3]) 

>>> X_dot_W + B  
array([[1, 2, 3], 
	[11, 12, 13]])

순전파의 편향 덧셈은 각각의 데이터(1번째 데이터, 2번째 데이터, ...)에 더해진다. 그래서 역전파 때는 각 데이터의 역전파 값이 편향의 원소에 모여야 한다.

dY = np.array([[1, 2, 3], [4, 5, 6]]) 
dB = np.sum(dY, axis=0) # [5, 7, 9]

편향의 역전파는 그 두 데이터에 대한 미분을 데이터마다 더해서 구한다. 그래서 np.sum()에서 0번째 축에 대해(axit=0) 총합을 구한다.

이상의 Affine 구현은 다음과 같다.

class Affine: 
	def __init__(self): 
    		self.W = W 
                self.b = b 
                self.x = None 
                self.original_x_shape = None 

                # 가중치와 편향 매개변수의 미분 
                self.dW = None 
                self.db = None 
        
    	def forward(self, x): 
        	self.x = x 
            	out = np.dot(x, self.W) + self.b 
                
                return out 
                
        def backward(self, dout): 
        	dx = np.dot(dout, self.W.T) 
            	self.dW = np.dot(self.x.T, dout) 
                self.db = np.sum(dout, axit=0) 
                
                return dx

softmax-with-loss 계층

마지막에서 출력층에서 사용하는 소프트맥스 함수에 대해 알아보자. 소프트맥스 함수는 입력 값을 경규화아혀 출력한다. 예를 들어 손글씨 숫자 인식에서의 출력은 다음과 같다.

위와 같이 Softmax 계층은 입력 값을 정규화(출력의 합이 1이 되도록 변형)하여 출력한다. 손글씨 숫자는 가짓수가 10개(10 클래스 분류)이므로 Softmax 계층의 입력은 10개가 된다.

신경망에서 수행하는 작업은 학습과 추론 두 가지이다. 추론할 때는 일반적으로 Softmax 계층을 사용하지 않는다. 예를 들어, 위에서 신경망은 추론할 때 마지막 Affine 계층의 출력을 인식 결과로 이용한다. 또한, 신경망에서 정규화하지 않는 출력 결과(Affine 계층의 출력)를 점수(Score)라고 한다. 즉, 신경망 추론에서 답을 하나만 내는 경우에는 가장 높은 점수만 알면 되니 Softmax 계층은 필요 없다는 것이다. 반면, 신경망을 학습할 때는 Softmax 계층이 필요하다.

이제 손실 함수인 교차 엔트로피 오차도 포함하여 'Softmax-with-Loss 계층'이라는 이름으로 구현해보자. 계산 그래프는 다음과 같다.

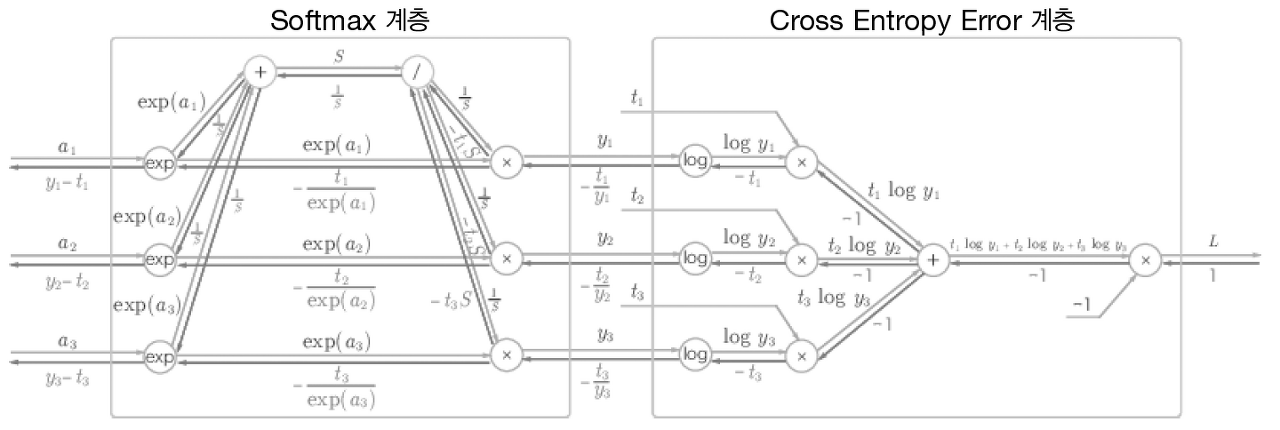
위의 계산 그래프는 다음과 같이 간소화할 수 있다.

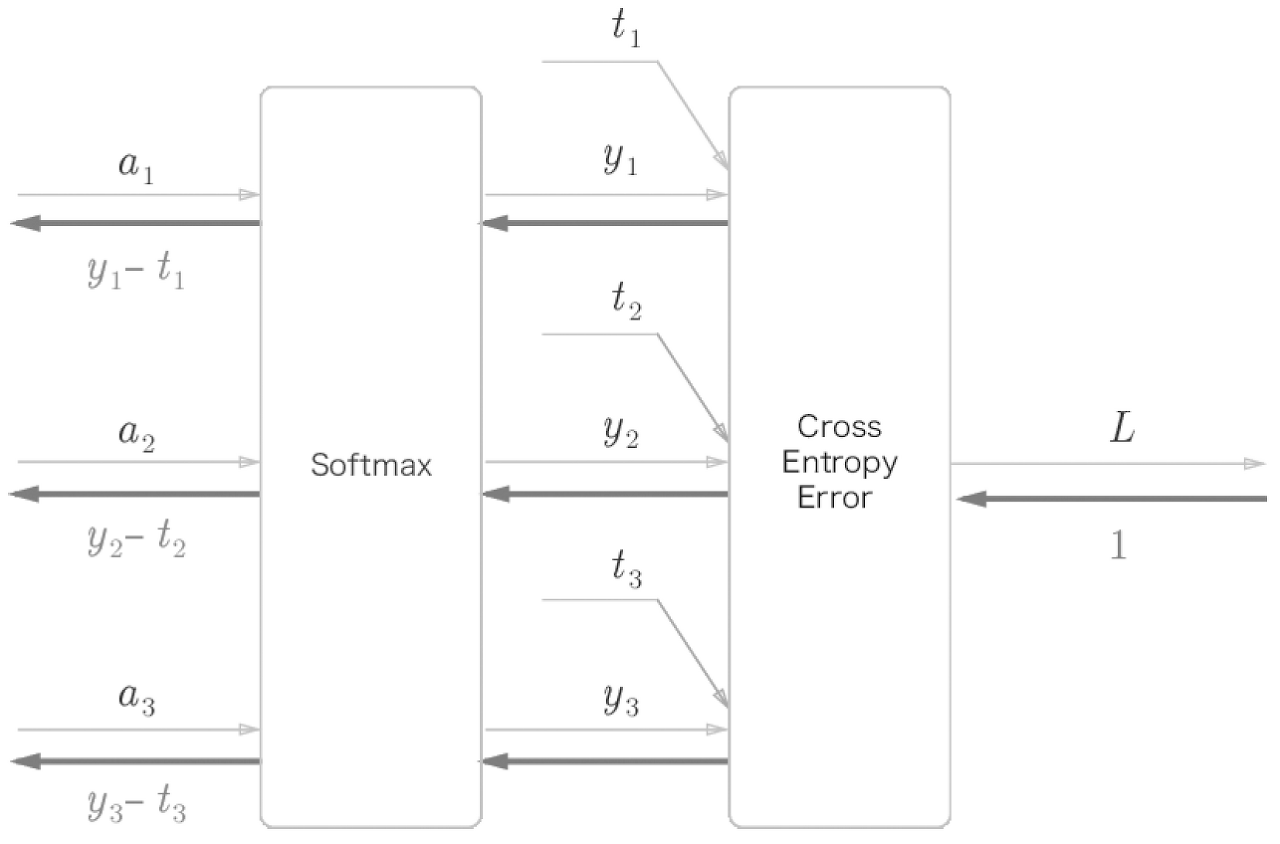
위의 계산 그래프에서 소프트맥스 함수는 'Softmax' 계층으로, 교차 엔트로피 오차는 'Cross Entropy Error' 계층으로 표시했다. 여기에서는 3클래스 분류를 가정하고 이전 계층에서 3개의 입력(점수)을 받는다. 그림과 같이 Softmax 계층은 입력 ( $a_1$ , $a_2$ , $a_3$ )를 정규화하여 ( $y_1$ , $y_2$ , $y_3$ )를 출력한다. Cross Entropy Error 계층은 Softmax의 출력 ( $y_1$ , $y_2$ , $y_3$ )와 정답 레이블 ( $t_1$ , $t_2$ , $t_3$ )를 받고, 이 데이터들로부터 손실 $L$ 을 출력한다.

여기서 주목할 것은 역전파의 결과이다. Softmax 계층의 역전파는 ( $y_1-t_1$ , $y_2-t_2$ , $y_3-t_3$ )라는 말끔한 결과를 내놓고 있다. ( $y_1$ , $y_2$ , $y_3$ )는 Softmax 계층의 출력이고 ( $t_1$ , $t_2$ , $t_3$ )는 정답 레이블이므로 ( $y_1-t_1$ , $y_2-t_2$ , $y_3-t_3$ )는 Softmax 계층의 출력과 정답 레이블의 차분인 것이다. 신경망의 역전파에서는 이 차이인 오차가 앞 계층에 전해지는 것이다. 이것은 신경망 학습의 중요한 성질이다.

그런데 신경망 학습의 목적은 신경망의 출력(Softmax의 출력)이 정답 레이블과 가까워지도록 가중치 매개변수의 값을 조정하는 것이었다. 그래서 신경망의 출력과 정답 레이블의 오차를 효율적으로 앞 계층에 전달해야 한다. 앞의 ( $y_1-t_1$ , $y_2-t_2$ , $y_3-t_3$ )라는 결과는 바로 Softmax 계층의 출력과 정답 레이블의 차이로, 신경망의 현재 출력과 정답 레이블 오차를 있는 그대로 드러내고 있다.

소프트맥스 함수의 손실 함수로 교차 엔트로피 오차를 사용하니 역전파가 ( $y_1-t_1$ , $y_2-t_2$ , $y_3-t_3$ )로 말끔히 떨어진다.

예를 들어, 정답 레이블이 (0, 1, 0)일 때 Softmax 계층이 (0.3, 0.2, 0.5)를 출력했다고 해보자. 정답 레이블을 보면 정답의 인덱스는 1이다. 그런데 출력에서는 이때의 확률이 겨우 0.2(20%)라서, 이 시점의 신경망은 제대로 인식하지 못하고 있다. 이 경우 Softmax 계층의 역전파는 (0.3, -0.8, 0.5)라는 커다란 오차를 전파한다. 결과적으로 Softmax 계층의 앞 계층들은 그 큰 오차로부터 큰 깨달음을 얻게 된다.

만약 정답 레이블은 (0, 1, 0)이고 Softmax 계층이 (0.01, 0.99, 0)을 출력한 경우가 있다고 해보자. 이 경우, Softmax 계층의 역전파가 보내는 오차는 비교적 작은 (0.01, -0.01, 0)이다.

class SoftmaxWithLoss: 
	def __init__(self): 
    	self.loss = None # 손실 
        self.y = None # softmax의 출력 
        self.t = None # 정답 레이블(원-핫 벡터) 
        
    def forward(self, x, t): 
    	self.t = t 
        self.y = softmax(x) 
        self.loss = corss_entropy_error(self.y, self.t) 
        
        return self.loss 
        
    def backward(self, dout=1): 
        batch_size = self.t.shape[0] 
        dx = (self.y - self.t) / batch_Size 

        return dx

괴도소녀

이전 포스트

4장-2. 신경망 학습

다음 포스트