최근 그래프 쪽 알고리즘 문제를 풀다가 인접리스트에서 LinkedList 대신 HashMap을 쓰면 더 효율적이지 않을까 하는 생각이 들었습니다.
관련 내용에 대해 찾아봤지만 생각보다는 이에 대한 논의가 적었고, 또 뚜렷한 결론이 없었습니다.
그래도 몇 개의 글과 실험을 통해 정리할 수 있어서, 이에 대해 기록해두려 합니다.
먼저 인접행렬과 인접리스트를 간단하게 비교해보겠습니다.
인접행렬 vs 인접리스트
대부분 그래프를 구현하는 방법으로 인접행렬과 인접리스트 2가지를 접할 것입니다.
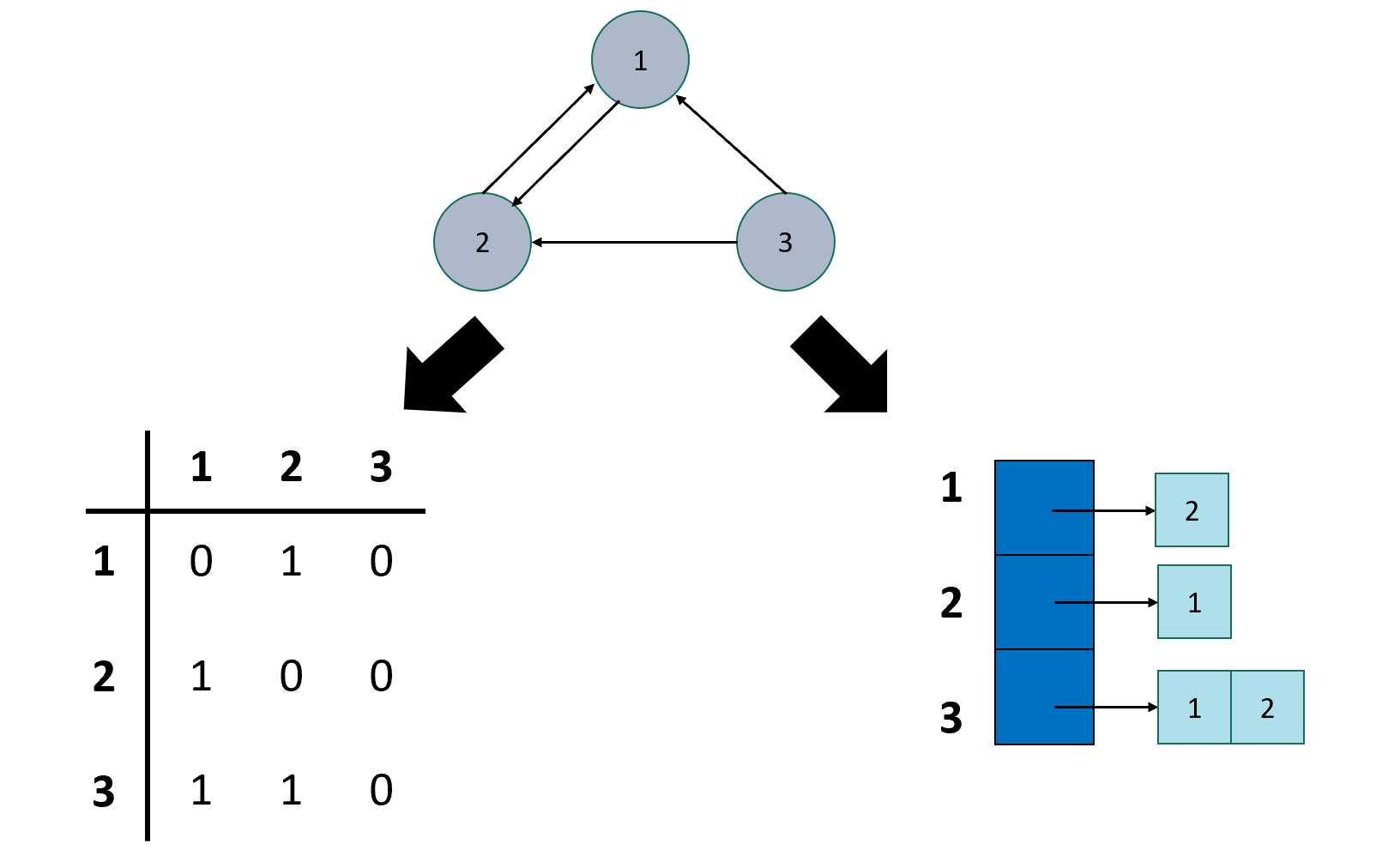정점의 수가 N이라고 할 때,
인접행렬은 N x N 크기의 이차원 배열을 통해 그래프를 나타냅니다.
arr[i][j]의 값을 확인하면 정점 i에서 j 로 가는 연결 정보를 확인할 수 있는 방식이죠.
인접리스트는 LinkedList를 통해 연결 정보를 나타냅니다.
list[i]가 참조하고 있는 list를 통해 i와 연결된 정점들을 확인할 수 있는 방식입니다.
여러 연산에 대해 시간복잡도를 비교한 결과는 다음과 같습니다.
N은 정점의 수, E는 전체 간선의 수입니다.
| 인접행렬 | 인접리스트 | |
|---|---|---|
| 두 정점 U와 V의 연결정보 확인 | O(1) | O(degree(U)) or O(degree(V)) |
| 정점 V와 연결된 모든 정점 확인 | O(N) | O(degree(V)) |
| 그래프에 관한 질문 ex) 전체 간선은 몇개인가? 연결 그래프인가? | O(N^2) | O(N+E) |
따라서 보통은 다음과 같은 기준으로 어떠한 구현방식을 택할지 결정할 것입니다.
- E가 N^2 보다 작은, 즉 간선의 수가 적은 sparse한 경우라면 인접리스트가 효율적이다.
- E가 N^2 보다 큰, 즉 간선의 수가 많은 dense한 경우라면 인접행렬이 효율적이다.
- 인접행렬을 사용하면 두 정점간의 연결정보를 O(1)에 확인할 수 있다는 장점이 있다.
여기까지가 일반적으로 접할 수 있는 그래프에 대한 이론입니다.
HashMap을 이용한 인접리스트?
의문이 들었던 점은 인접리스트에서 두 정점 간의 연결정보를 찾는 시간복잡도가 O(degree(v))라는 점입니다.
'Hashing을 이용하면, O(1)의 시간복잡도로 조회가 가능하지 않을까'하는 생각이 들었죠.
결론적으로 말하면, 인접리스트에서도 HashMap 또는 HashSet을 이용하면 두 정점간의 연결정보를 O(1)의 시간복잡도로 확인할 수 있습니다.
(물론 LinkedList가 아니라 HashMap을 이용한 구조를 인접리스트라고 해도 될지는 애매합니다.)
당연하게 O(degree(v))로 알고 있었기 때문에, 처음에는 정말 그런가? 싶겠지만 코드를 보면 쉽게 사실이라는 것을 알 수 있습니다.
Set을 이용하여 앞선 표의 연산들을 구현하면 다음과 같은 모습일 것입니다(psedo-code).
// 선언
List<Set<Integer>> adjList = new ArrayList<>();
//두 정점 U와 V의 연결정보 확인
adjList.get(U).get(V); // O(1)
//정점 V와 연결된 모든 정점 확인
for(Integer adj : adjList.get(U)){ //O(degree(V))
// do something
}
만약 가중치 그래프라면 다음과 같을 것입니다.
//선언
List<HashMap<Integer, Integer>> adjList = new ArrayList<>(); // 정점 번호, weight
// 두 정점 U와 V의 연결정보 확인
adjList.get(U).get(V);글을 작성하며 생각해보니, 메모리만 여유롭다면 인접행렬과 인접리스트 두 방식을 모두 사용하고, 연산에 따라 더욱 유리한 방식으로 읽어오는 방법도 생각해 볼 수 있네요.
따라서 시간복잡도를 낮출 수 있다는 것 자체는 그렇게 놀랍지 않을 수 있지만, 그렇다면 왜 'LinkedList를 이용한 방법이 더 일반적이지?' 하는 여전히 의문이 들었다.
이에 대해 이런저런 내용들을 찾아본 결과, LinkedList를 사용하는 것이 유리한 몇가지 이유가 있었습니다.
(1) 가장 근본적으로, HashMap.get의 시간복잡도는 반드시 O(1)이 아닙니다.
사실상 O(1)에 가깝지만, 충돌 등이 발생하는 경우를 고려해야 합니다.
(https://stackoverflow.com/questions/4553624/hashmap-get-put-complexity)
(2) 대부분의 그래프 알고리즘에서 특정 간선을 조회하는 경우는 드뭅니다. 대표적으로 DFS가 있겠네요.
(실제로 이 문제를 처음 고민하게 된 것도 다익스트라 관련 문제였는데, 다익스트라 알고리즘에서도 특정 간선을 조회할 필요가 없습니다.)
(3) 어떠한 정점 V와 인접한 정점을 조회하는 것은 LinkedList가 더 빠릅니다. (0)의 이유를 생각하면 된다.
실제로 그런지 확인해보기 위해서 다음 코드로 실험을 진행해봤습니다.
import java.util.*;
class Pair{
int key;
int weight;
Pair(int key, int weight){
this.key = key;
this.weight = weight;
}
}
class Main {
static public void hashingTest(int testNum){
HashMap<Integer, Integer> map = new HashMap<>();
for(int i = 0 ; i < testNum; i++){
map.put(i, i);
}
long start = System.currentTimeMillis();
for(Integer key : map.keySet()){
int weight = map.get(key);
}
long end = System.currentTimeMillis();
System.out.println("HashMap : " + (end-start) + "ms");
}
static public void linkedListTest(int testNum){
LinkedList<Pair> list = new LinkedList<>();
for(int i = 0; i < testNum; i++){
list.add(new Pair(i, i));
}
long start = System.currentTimeMillis();
for(Pair p : list){
int weight = p.weight;
}
long end = System.currentTimeMillis();
System.out.println("LinkedList : " + (end-start) + "ms");
}
public static void main(String[] args) {
int testNum = 1000000;
System.out.println("number of data: " + testNum);
hashingTest(testNum);
linkedListTest(testNum);
}
}
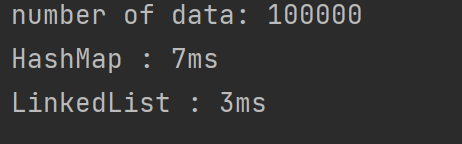
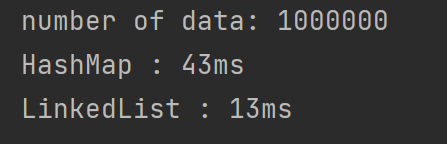
LinkedList를 이용한 방법이 2배~3배 정도 더 빠른 것을 확인할 수 있습니다.
정리하자면, 시간복잡도를 떠나서 LinkedList를 이용한 방법이 실용적이라고 정리할 수 있겠습니다.
그러나 절대적인 것은 아니였고, 경우에 따라서는 해싱을 이용한 방법을 통해 효과를 볼 수 있을 것 같습니다.
결론
- 인접리스트에서 LinkedList 대신 HashMap을 이용하면 사실상 O(1)의 시간복잡도로 두 정점간의 연결 정보를 얻을 수 있다.
- 그러나 대부분의 실용적인 연산에서는 LinkedList를 이용한 방법이 여전히 더 효율적이다.
