[알고리즘] 세그먼트 트리 (Segment Tree)

1. 세그먼트 트리

: 여러 개의 데이터가 연속적으로 존재할 때 특정 범위 데이터의 합을 빠르고 간단하게 구할 수 있는 자료구조

2. 배열에서 특정 구간 합 구하기

1) 단순 배열을 이용해 선형적으로 구하기
: 범위 내 값을 하나씩 더해가면서 구할 수 있다. 이 때 데이터 개수가 N개이면 시간 복잡도는 O(N)이 된다. 이 경우에는 구간 합을 구하는 속도가 너무 느리기 때문에 더 나은 알고리즘을 고안해야 한다.

2) 세그먼트 트리를 이용해 구하기
: 트리 구조 특성 상 N개 데이터의 합을 구할 때 시간 복잡도가 O(logN)이 된다.

3. 세그먼트 트리를 이용한 구간 합

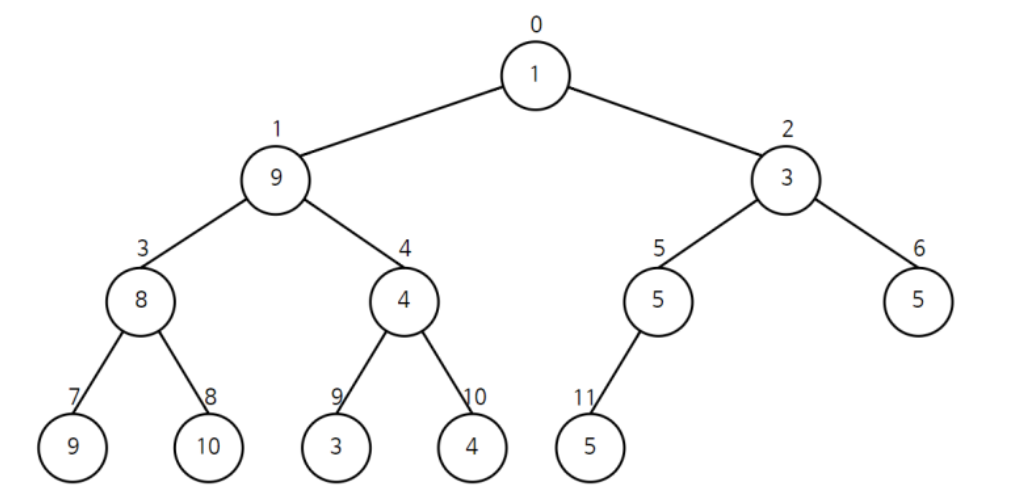
단순 배열을 위와 같은 트리 구조로 변경했을 때 구간 합을 구하는 방법을 알아볼 것이다.

1) 구간 합 트리 생성하기

• 가장 먼저 최상단 노드에 전체 원소(0 ~ 11)를 더한 값을 삽입한다.
  

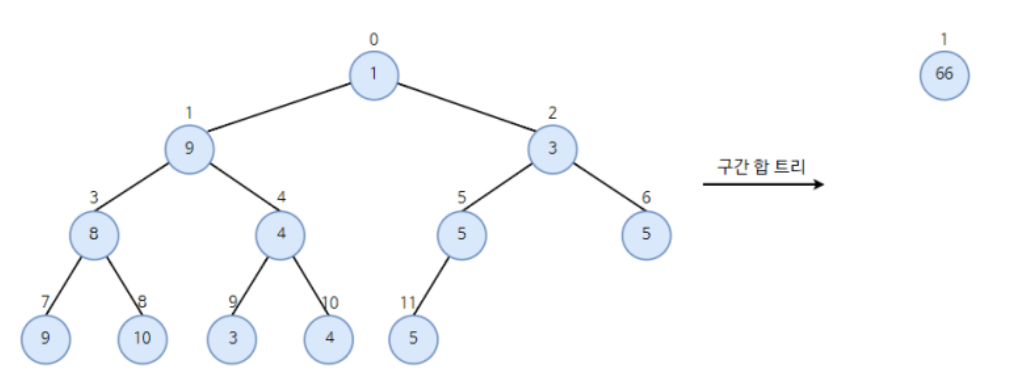
• 이후 최상단 노드의 양쪽 자식 노드에 각각 인덱스 0 ~ 5 원소의 합, 인덱스 6 ~ 11 원소의 합을 삽입한다.
  

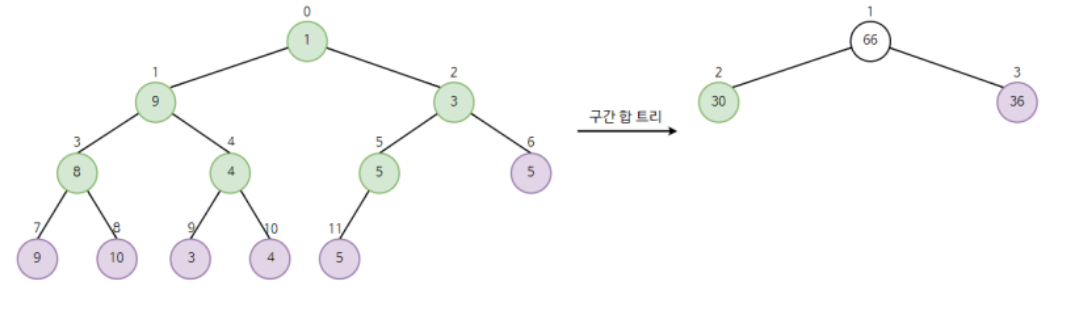
• 위와 같이 부모 노드의 데이터 범위를 반씩 분할하여 그 구간의 합들을 저장하는 방식으로 트리를 채워 나가는 것이다. 이러한 과정을 반복하면 구간 합 트리의 전체 노드를 구할 수 있다.

  • 부모 노드의 데이터 범위를 start ~ end 라고 하면
  • 부모 노드 크기를 반으로 분할 : mid = (start + end) / 2
  • 자식 노드 중 왼쪽 노드는 start ~ mid / 오른쪽 노드는 mid + 1 ~ end
    

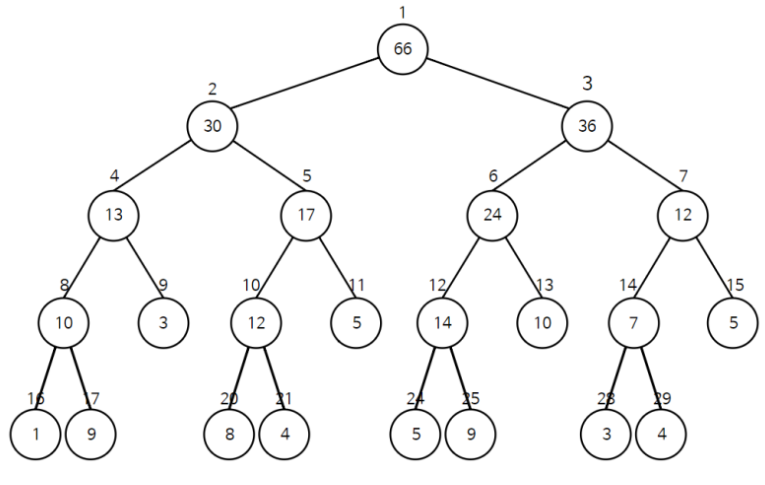
• 구간 합 트리를 만들 때는 인덱스 번호를 1로 시작한다.

  • 데이터의 인덱스는 0부터 시작하지만, 구간 합 트리를 1부터 시작하면 부모 노드 번호에 2를 곱하면 왼쪽 자식 노드를 가리키므로 인덱스를 설정하기 편하기 때문이다.

• 데이터의 개수가 N개일 때, 구간 합 트리는 N보다 큰 가장 가까운 제곱수를 구한 뒤, 그 수의 2배의 크기를 가져야 한다.

  • ex. 데이터의 개수가 12개라면, 12보다 큰 가장 가까운 제곱수는 16
  • 16 x 2 = 32이므로 구간 합 트리의 크기는 32이다.
  • 계산하기 귀찮다면 데이터 개수 x 4를 해주면 메모리를 조금 더 먹지만 편리하게 계산 가능하다.

🖥️ 예제 코드

int tree[32];
int datas[12];

// start : 범위 시작 / end : 범위 끝 / node : 현재 구간합 트리 노드 번호
int init(int start, int end, int node)
{
	// 범위에 수가 하나 남을 때까지 분할하고, 하나 남으면 해당 수 반환
	if (start == end) return tree[node] = datas[start];
	int mid = (start + end) / 2;
	// 현재 노드의 범위를 재귀적으로 반으로 분할하여 두 부분의 합을 자기 자신으로 할당
	return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}

2) 구간 합을 구하는 함수 만들기

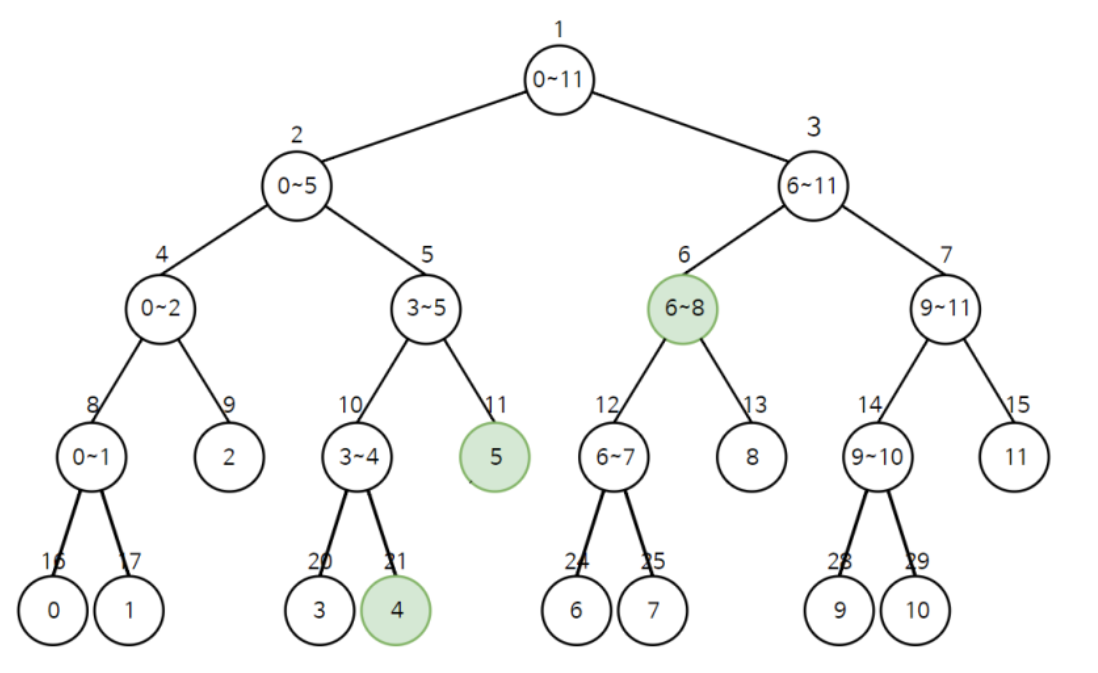
• 만약 4 ~ 8 범위에 대한 합을 구한다고 하면 색칠 된 노드들의 값만 더해주면 된다.

🖥️ 예제 코드

// 범위 안에 있는 경우에 한해서만 더해주면 된다.
// start : 범위 시작 / end : 범위 끝 // node : 현재 구간합 트리 노드 번호
// left : 구하고자 하는 범위 시작 / right : 구하고자 하는 범위 끝
int sum(int start, int end, int node, int left, int right)
{
	// 범위 밖에 있는 경우
	if (left > end || right < start) return 0;
	// 범위 안에 있는 경우
	if (left <= start && end <= right) return tree[node];
	// 범위에 걸쳐있는 경우 두 부분으로 나누어 합 구하기
	int mid = (start + end) / 2;
	return sum(start, mid, node * 2, left, right) 
		+ sum(mid + 1, end, node * 2 + 1, left, right);
}

3) 특정 원소 값을 수정하는 함수 만들기

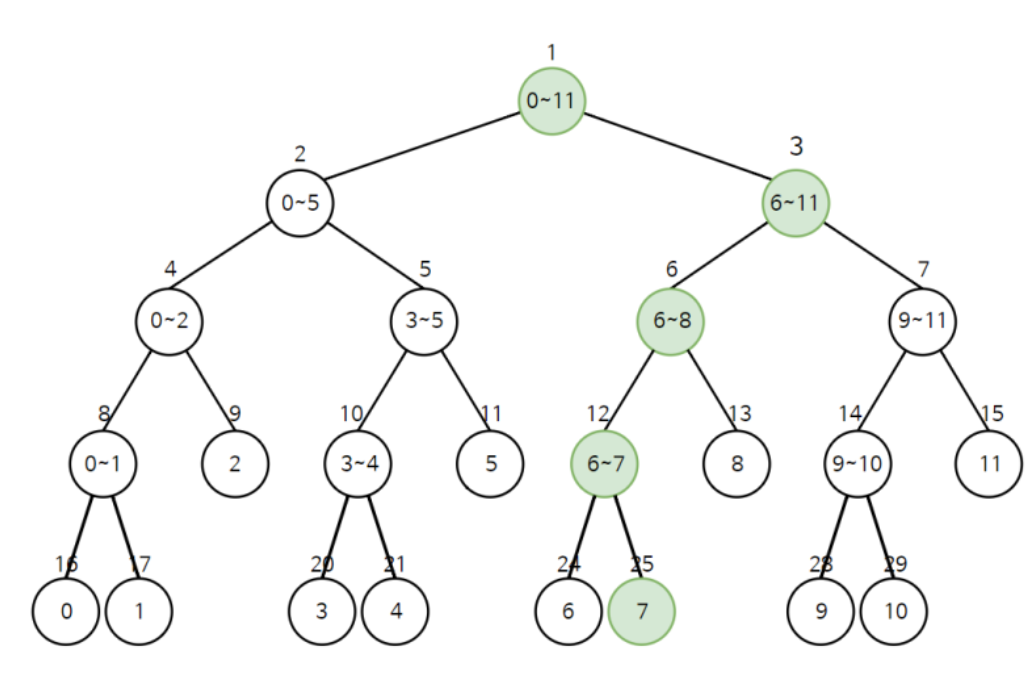
• 특정 원소 값을 수정할 때는 해당 원소를 포함하고 있는 모든 구간 합 노드들을 갱신해준다.
• 만약 인덱스 7의 노드를 수정한다고 하면 색칠 된 노드들의 값만 수정하면 된다.

🖥️ 예제 코드

// index : 값을 수정하고자 하는 노드 / dif : 수정할 값
void update(int start, int end, int node, int index, int dif)
{
	// 범위 밖에 있는 경우
	if (index < start || index > end) return;
	// 범위 안에 있으면 내려가며 다른 원소도 갱신
	tree[node] += dif;
	if (start == end) return;
	int mid = (start + end) / 2;
	update(start, mid, node * 2, index, dif);
	update(mid + 1, end, node * 2 + 1, index, dif);
}

4) 모든 과정 취합 코드

int tree[32];
int datas[12] = { 1, 9, 3, 8, 4, 5, 5, 9, 10, 3, 4, 5 };

// start : 범위 시작 / end : 범위 끝 / node : 현재 구간합 트리 노드 번호
int init(int start, int end, int node)
{
	// 범위에 수가 하나 남을 때까지 분할하고, 하나 남으면 해당 수 반환
	if (start == end) return tree[node] = datas[start];
	int mid = (start + end) / 2;
	// 현재 노드의 범위를 재귀적으로 반으로 분할하여 두 부분의 합을 자기 자신으로 할당
	return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}

// 범위 안에 있는 경우에 한해서만 더해주면 된다.
// start : 범위 시작 / end : 범위 끝 // node : 현재 구간합 트리 노드 번호
// left : 구하고자 하는 범위 시작 / right : 구하고자 하는 범위 끝
int sum(int start, int end, int node, int left, int right)
{
	// 범위 밖에 있는 경우
	if (left > end || right < start) return 0;
	// 범위 안에 있는 경우
	if (left <= start && end <= right) return tree[node];
	// 범위에 걸쳐있는 경우 두 부분으로 나누어 합 구하기
	int mid = (start + end) / 2;
	return sum(start, mid, node * 2, left, right) 
		+ sum(mid + 1, end, node * 2 + 1, left, right);
}

// index : 값을 수정하고자 하는 노드 / dif : 수정할 값
void update(int start, int end, int node, int index, int dif)
{
	// 범위 밖에 있는 경우
	if (index < start || index > end) return;
	// 범위 안에 있으면 내려가며 다른 원소도 갱신
	tree[node] += dif;
	if (start == end) return;
	int mid = (start + end) / 2;
	update(start, mid, node * 2, index, dif);
	update(mid + 1, end, node * 2 + 1, index, dif);
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);

	init(0, 11, 1);
	// 구간 합 구하기
	cout << "0 ~ 12 구간 합 : " << sum(0, 11, 1, 0, 11) << endl;
	cout << "4 ~ 8 구간 합 : " << sum(0, 11, 1, 4, 8) << endl;
	
	// 특정 원소 값 수정하기
	cout << "인덱스 5의 원소 -5만큼 수정" << endl;
	update(0, 11, 1, 5, -5);

	// 구간 합 구하기
	cout << "0 ~ 12 구간 합 : " << sum(0, 11, 1, 0, 11) << endl;
}

[출력 결과]
0 ~ 12 구간 합 : 66
4 ~ 8 구간 합 : 33
인덱스 5의 원소 -5만큼 수정
0 ~ 12 구간 합 : 61

👁️‍🗨️ 참고
https://m.blog.naver.com/ndb796/221282210534