[알고리즘] LCS 알고리즘인데 DP를 이용한

LCS 알고리즘(Longest Common Subsequence)

• LCS == 최장 공통 부분 수열로, 두 문자열을 비교했을 때 가장 긴 공통 부분 문자열
• LCS는 최장 공통 문자열(Longest Common String)을 의미하기도 하는데, 둘의 차이점은 공통 부분이 연속하는지 아닌지 여부다.
• 두 문자열 ABCD, ABFC 가 있다고 할 때,
  • 최장 공통 문자열 : AB
  • 최장 공통 부분 수열 : ABC

  ---

✍️ DP를 이용한 LCS 풀이 방법

: DP[i][j]에는 i 인덱스까지의 문자열 1과 j인덱스까지의 문자열 2 사이의 LCS의 길이가 저장된다.

• 문자열 BCFD와 ABCD를 비교한다고 할 때
  • 각 문자열의 세번째 인덱스까지의 LCS는 아래 두 가지 중 하나로 결정된다.
    • 세 번째 글자가 같다면 : BC와 AB 사이의 LCS + 1
      • 같은 글자라면 공통 부분에 포함되기 때문에 세 번째 글자가 LCS에도 추가된다.
      • 점화식 : dp[i][j] = dp[i - 1][j - 1] + 1
    • 세 번째 글자가 다르다면 : BCF, AB 사이의 LCS / BC, ABC 사이의 LCS 중 더 길이가 긴 것
      • 다른 글자라면 LCS에 포함되지 않기 때문에 이전까지의 LCS와 동일하다.
      • 점화식 : dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

1) (문자열 1의 길이 + 1) * (문자열 2의 길이 + 1) 크기의 2차원의 dp 배열을 만들고 모든 칸을 0으로 초기화한다.

• 계산의 편리성을 위해 배열을 문자열의 길이보다 1 크게 만든다.

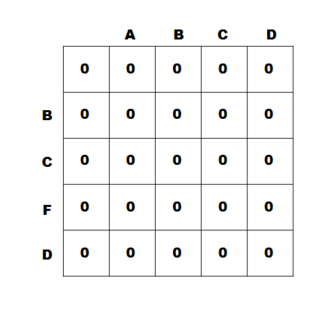
• 이제부터 문자열 1의 길이 = i, 문자열 2의 길이 == j라고 표시하겠다.

2) i = 1, j = 1일 때

• 두 글자가 같지 않기 때문에 dp[1][1] = max(dp[1 - 1][1], dp[1][1 - 1]) = 0

3) i = 1, j = 2일 때

• 두 글자가 같기 때문에 dp[1][2] = dp[1 - 1][2 - 1] + 1 = 1

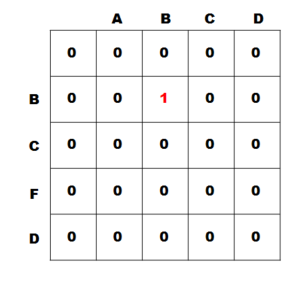
4) i = 1, j = 3일 때

• 두 글자가 같지 않기 때문에 dp[1][3] = max(dp[1 - 1][3], dp[1][3 - 1]) = 1

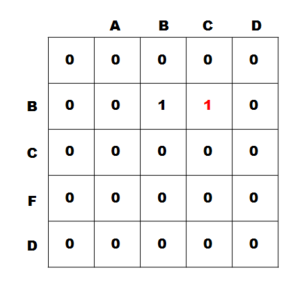
5) i = 1, j = 4일 때

• 두 글자가 같지 않기 때문에 dp[1][4] = max(dp[1 - 1][4], dp[1][4 - 1]) = 1

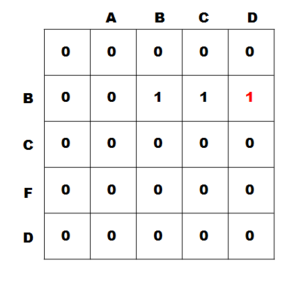
6) i = 2, j = 1일 때

• 두 글자가 같지 않기 때문에 dp[2][1] = max(dp[2 - 1][1], dp[2][1 - 1]) = 0

7) i = 2, j = 2일 때

• 두 글자가 같지 않기 때문에 dp[2][2] = max(dp[2 - 1][2], dp[2][2 - 1]) = 1

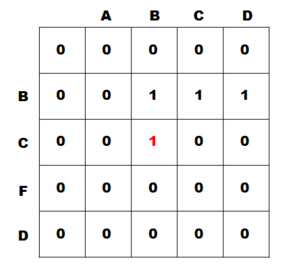
8) i = 2, j = 3일 때

• 두 글자가 같기 때문에 dp[2][3] = dp[2 - 1][3 - 1] + 1 = 2

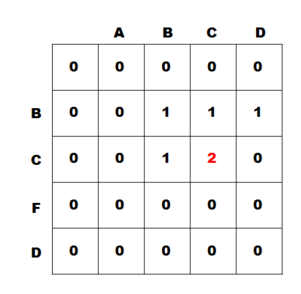
9) i = 2, j = 4일 때

• 두 글자가 같지 않기 때문에 dp[2][4] = max(dp[2 - 1][4], dp[2][4 - 1]) = 2

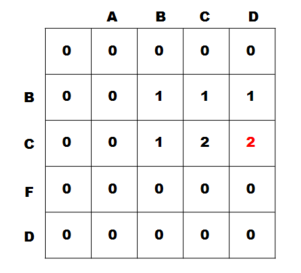
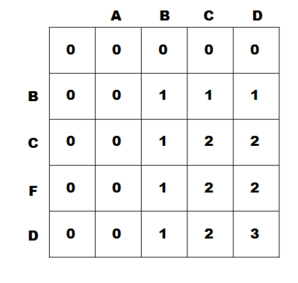
10) 위와 같은 과정을 계속 반복하면 최종적으로 아래와 같은 dp 배열이 완성된다. 여기서 최장 공통 부분 수열의 길이는 dp 내에서 가장 큰 값인 3이 된다.

---

🖥️ 구현 코드

• 백준 9251번 : LCS(https://www.acmicpc.net/problem/9251)와 동일한 코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>

using namespace std;
vector<char> string1;
vector<char> string2;
int dp[1001][1001];

int solution()
{
	for (int i = 1; i <= string1.size(); i++)
	{
		for (int j = 1; j <= string2.size(); j++)
		{
			if (string1[i - 1] == string2[j - 1])
				dp[i][j] = dp[i - 1][j - 1] + 1;
			else
				dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
		}
	}

	int max = 0;
	for (int i = 1; i <= string1.size(); i++)
	{
		for (int j = 1; j <= string2.size(); j++)
		{
			if (max < dp[i][j])
				max = dp[i][j];
		}
	}
	return max;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);

	string str1, str2;
	cin >> str1 >> str2;

	for (int i = 0; i < str1.size(); i++)
		string1.push_back(str1[i]);
	
	for (int i = 0; i < str2.size(); i++)
		string2.push_back(str2[i]);

	cout << solution();
}

---

👁️‍🗨️ 참고
https://twinw.tistory.com/126
https://velog.io/@emplam27/알고리즘-그림으로-알아보는-LCS-알고리즘-Longest-Common-Substring와-Longest-Common-Subsequence